Вектор умова пойнтинга его физический смысл

4.3.018 Поток энергии Умова
(к сожалению, формулы воспроизводятся не точно)

Физик, философ, педагог, лектор, пропагандист, популяризатор науки, общественный деятель; профессор Новороссийского и Московского университетов, Московского технического училища; почетный доктор Глазговского университета; основатель (совместно с П.Н. Лебедевым) Физического института при Московском университете; президент Московского общества испытателей природы, председатель Московского педагогического общества, товарищ председателя «Общества содействия успехам опытных наук и практических применений им. Х.С. Леденцова»; издатель и главный редактор журнала «Научное слово» — Николай Алексеевич Умов (1846—1915) является автором учения о движении энергии в телах, базового понятия в новейшей физике — потока энергии, т.н. вектора Умова.

Умов — первооткрыватель классической формулы общего уравнения движения энергии.

Человечество с каждым годом все больше нуждается в энергии — механической, тепловой, химической, электрической, ядерной. Все эти формы энергии, трансформируясь друг в друга, дают совокупность энергетических процессов, без которых не обойтись ни обывателям, ни ученым. Последних всегда интересовал вопрос — каким образом происходит эта трансформация и как повысить ее к.п.д.

Схематично это выглядит так. В замкнутый объем через поверхность поступает первичная энергия, а затем выходит преобразованная (разумеется, в рамках закона сохранения энергии). Плотность потока энергии (Su) при этом ограничена физическими свойствами среды, через которую она течет.

Этот термин — плотность потока энергии ввел в начале 1870-х гг. русский физик Н.А. Умов, опубликовавший несколько работ о движении энергии, в которых развил представления о плотности энергии в данной точке среды, скорости и направлении движения энергии, о локализации потока энергии в пространстве.

Ученый составил дифференциальные уравнения движения энергии в твердых телах постоянной упругости и в жидких телах, интегрируя которые и применяя к распространению волн в упругой среде, пришел к заключению, что энергия целиком переносится волной от одной точки к другой.

«Количество энергии, проходящей через элемент поверхности тела в единицу времени, равно силе давления или натяжения, действующей на этот элемент, умноженной на скорость движения элемента» — этот вывод называется теоремой Умова.

Уравнение непрерывности в свободном пространстве для движущихся упругих сред и вязких жидкостей имеет вид:

dw/dt + div Su = 0,

где Su = wv; w — плотность энергии; v — скорость движения среды.

После защиты ученым в 1874 г. докторской диссертации «Уравнения движения энергии в телах» Su принято называть в нашей стране вектором Умова.

В 1884 г. английский физик Д. Пойнтинг, независимо от Умова и ничего не зная о трудах русского ученого, получил подобное выражение для частного случая — электромагнитного поля (поперечных электромагнитных волн). На Западе без особых рефлексий вектор Умова переименовали в вектор Пойнтинга (Sp).

Sp = [E ; H]; E и H — напряженности электрического и магнитного полей.

Сам Умов, кстати, отмечал, что его выводы применимы и в электромагнитных полях.

Необходимо различать принципиальную разницу между этими понятиями — Su и Sp. Вектор Пойнтинга можно рассматривать только применительно к электромагнитным полям, тогда как вектор Умова применим ко всем силовым полям без исключения, поскольку сами уравнения движения энергии получены Умовым для движения любого вида энергии, происходящего в любой среде, т.е. носят самый общий характер.

Не прибегая к выкладкам, заметим еще, что вектор Умова Su описывает конвективный перенос энергии из одной точки пространства в другую, в частности, полем движущегося заряда; а вектор Пойнтинга связан лишь с переносом энергии электромагнитными волнами.

Труды Умова своей математической сложностью представляли «крепкий орешек» для российских и зарубежных коллег Николая Алексеевича. Утверждали даже, что они «лишены какого бы то ни было научного смысла и представляют собой… простой набор математических формул». Раскусили их не сразу, но, раскусив, буквально растащили на цитаты, при этом не всегда озвучивая автора.

Так было и в других случаях. Когда Умов показал свою блестящую работу «О стационарном движении электричества на проводящих поверхностях произвольного вида» немецкому физику Г. Кирхгофу, тот тут же умыкнул главные положения этого исследования и опубликовал их под своим именем (не забыв, правда, упомянуть и русского ученого).

Фактически то же самое произошло и со знаменитой формулой E = mc2, которую русский физик получил лет за тридцать до А. Эйнштейна — опять же как общий случай для волновых процессов в упругих средах. (Умов вывел соотношение между энергией волновых полей и их инерцией: dE = c2dm).

Но вернемся к вектору и к области его применения. Надо сказать, что область эта — широчайшая, как в науке, так и в технике. Без вектора Умова не обойтись при освоении нового вида энергии (скажем, термоядерной), при разработке сложного и дорогостоящего технического устройства (ТОКОМАК).

35 лет назад, в преддверии глобального мирового энергетического кризиса из-за исчерпания природных энергетических ресурсов, П.Л. Капица в одном из своих докладов, посвященных энергетической проблеме, обосновывая свои положения в выборе того или иного вида энергии, оперировал только вектором Умова.

Рассматривая альтернативные способы получения энергии, академик подчеркивал удобство вектора Умова для изучения процессов преобразования энергии. При этом Капица привел примеры, как с помощью этого вектора определяют предельную мощность мотора или турбины; мощность трансмиссии ременной передачи; предельную мощность, передаваемую лентой в генераторе типа Ван-де-Граафа; предельную мощность в газовых, химических элементах, в солнечных батареях, геотермальных источниках; как находят предельную высоту, на которой может летать турбореактивный самолет и т.д.

К сказанному Капицей можно добавить, что вектор Умова применяют для проектирования электромагнитных излучателей и направляющих систем в радиоэлектронной аппаратуре, для расчета энергетических характеристик антенн, в частности, сопротивления излучения выпускных самолетных антенн.

Вектор необходим при определении оптимальной аэродинамической конструкции летательного аппарата в поле скоростей. В процессах и аппаратах химических технологий его используют для составления детерминированных и идеальных математических моделей. В электротехнике с его помощью определяют внутреннее активное и реактивное сопротивление проводника. И т.д. и т.п.

«Представления Умова о движении и распределении энергии в средах, о ее потоке, скорости и направлении являются общепризнанными в современной физике. Они прочно завоевали себе место в таких ее разделах, как теория поля, электродинамика, оптика, акустика, гидродинамика… Именно Умов изложил очень ценную идею об универсальности всех силовых взаимодействий в природе» (профессор А.Л. Шаляпин).

Видео:Вектор Умова-Пойнтинга ● 1Скачать

Вектор Пойнтинга (вектор Умова — Пойнтинга)

Перенос энергии бегущей упругой и электромагнитной волной определяют при помощи вектора, который называют вектором потока энергии. Этот вектор обозначим как $overline $(встречается обозначение $overline

$) Он показывает количество энергии, протекающее в волне за единицу времени через единицу площади поперечного сечения волны. Для электромагнитных волн данный вектор был введен Пойнтингом в 1884 г. Скорость переноса энергии при помощи вектора Пойнтинга не изменяется и равна характеристической скорости распространения электромагнитной волны в пространстве. Сейчас данный вектор ($overline$) называют вектором Умова — Пойнтинга.

Видео:Вектор Умова-Пойнтинга ● 2Скачать

Определение

Вектором Умова — Пойнтинга ($overline$) называют физическую величину, определяющую поток энергии электромагнитного поля, который равен:

где $overline$ — напряженность электрического поля; $overline$ — напряженность магнитного поля. Направлен $overline$ перпендикулярно $overline$ и $overline$ и совпадает с направлением распространения электромагнитной волны.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Величина вектора Умова — Пойнтинга

Правая часть формулы (1) представляет собой векторное произведение векторов, значит, величина вектора Умова — Пойнтинга для электромагнитной волны равна:

где $alpha $ — угол между векторами $overline$ и $overline$, но $overlinebot $ $overline$, следовательно, получаем для электромагнитной волны:

Вектор $overline $удовлетворяет в свободном пространстве уравнению непрерывности:

где $w$ — объемная плотность энергии электромагнитного поля.

Видео:Вектор Умова Пойтинга или откуда берётся энергия в электромагнетизмеСкачать

Вектор Умова — Пойнтинга плоской электромагнитной волны

В случае плоской электромагнитной волны величина вектора $overline$ равна:

где $u$ $=frac<sqrt<_0mu varepsilon _0>>$- фазовая скорость распространения электромагнитного возмущения в веществе с диэлектрической проницаемостью $varepsilon $ и магнитной проницаемостью $mu .$

где $c$ — скорость света в вакууме.

Мгновенные величины напряженности магнитного и электрического полей в рассматриваемой волне связаны соотношением:

выразим напряженность $H$:

Учитывая формулу (8) величину вектора $overline$ запишем как:

В изотропном веществе объемную плотность энергии электромагнитного поля найдем как:

Учитывая формулы (6) и (10) запишем еще одно выражение для величины вектора $overline$:

На практике переходят от мгновенных величин к их средним значениям. Для плоской электромагнитной волны средняя величина по времени вектора Умова — Пойнтинга равна:

Модуль величины $left|_tright|$ называют интенсивностью ($I$) электромагнитной волны:

Направление вектора Умова — Пойнтинга показывает направление движения энергии в электромагнитном поле. Если изобразить линии, касательные к которым в любой точке совпадут с направлениями вектора $overline$, то такие линии будут являться путями распространения энергии электромагнитного поля. В оптике это лучи.

Видео:Вектор Умова-Пойнтинга ● 4Скачать

Примеры задач с решением

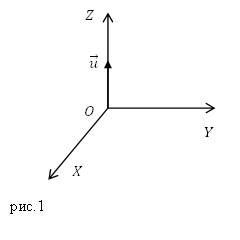
Задание. На рис.1 изображен вектор фазовой скорости плоской электромагнитной волны. В какой плоскости расположены векторы $overline$ и $overline$ полей этой волны?

Решение. Основой решения нашей задачи будем считать определение вектора $overline$:

Вектор $overline$ является результатом векторного произведения векторов$overline$ и $overline$, он направлен в сторону распространения электромагнитной волны, следовательно, $overlineuparrow uparrow overline$, для рис.1 вектор Умова — Пойнтинга направлен по оси Z. Значит, векторы $overlineи overline$ лежат в плоскости XOY.

Ответ. XOY

Задание. Запишите модуль среднего вектора Умова — Пойнтинга электромагнитной волны: $overline=E_0 $Считайте, что волна распространяется в вакууме по оси X.

Решение. Модуль вектора Умова — Пойнтинга для электромагнитной волны:

где $E$ и $H$ — мгновенные значения электрического и магнитного полей. Мгновенное значение вектора Умова — Пойнтинга будет равно:

[S=EH=E_0H_0<^2 left(omega t-kxright)(2.2), >]

где $H_0$ — амплитуда колебаний напряженности магнитного поля.

Средняя величина $_t$ может быть найдена:

принимая во внимание, что $<leftlangle <^2 left(omega t-kxright) >rightrangle >_t=frac$, для вакуума имеем:

Видео:Вектор Умова-Пойнтинга ● 3Скачать

Вектор Умова-Пойнтинга

Вы будете перенаправлены на Автор24

Вектор потока электромагнитной энергии, определяемый как:

называют вектором Умова — Пойнтинга (вектором Пойнтинга). Понятие вектора как потока энергии в разных веществах было введено Н.А. Умовым, а математическое выражение (1) получено Пойнтингом.

В электромагнитной волне векторы $overrightarrow и overrightarrow$ перпендикулярны, следовательно, модуль вектора $overrightarrow

$ имеет выражение:

Направление вектора Умова — Пойнтинга перпендикулярно к векторам $overrightarrowи overrightarrow$, и со направленно с направлением распространения волны ($overrightarrow$).

Для плоской электромагнитной волны выражение для модуля вектора Умова — Пойнтинга имеет вид:

и между мгновенными значениями напряженности магнитного и электрического полей в электромагнитной волне существует соотношение:

Модуль вектора Умова — Пойнтинга можно выразить как:

В диэлектрике объемная плотность электромагнитного поля равна:

Следовательно, сравнивая равенства (6) и (7), имеем:

В уравнения (2) -(8) входят мгновенные значения величин. Векторы в световой волне совершают колебания с частотами около $^Гц$, следовательно, весьма затруднительно следить за изменением величин во времени. Поэтому обращаются к средним значениям, переходя от мгновенных величин. Если электромагнитная волна является плоской, то среднее значение по времени вектора Умова — Пойнтинга равно:

Вектор Умова — Пойнтинга связан с энергией, которую несет электромагнитная волна соотношением:

где $frac$ — энергия, проходящая через площадку $S$ в единицу времени, $P_n=Pcosalpha $ — проекция вектора $overrightarrow

$ на нормаль $overrightarrow$ к площадке $S$. Направление вектора Умова — Пойнтинга дает характеристику движения энергии в электромагнитном поле.

Готовые работы на аналогичную тему

Если представить линии, касательные к которым в каждой точке совпадают с направлениями вектора $overrightarrow

$, то такие линии есть пути распространения энергии электромагнитного поля. В оптике подобные линии называют лучами.

Видео:Вектор Умова-Пойнтинга ● 5Скачать

Теорема Пойнтинга

Для теории электромагнитных полей формулировки законов сохранения энергии и импульса имеет весьма важное значение. Теорема Пойнтинга — один из видов формулировок закона сохранения энергии: Скорость возрастания электромагнитной энергии внутри некоторого объема в сумме с энергией, которая вытекает за единицу времени через поверхность, ограничивающую тот же объем, равна полной работе, которую совершает поле над источниками внутри заданного объема, если взять ее со знаком минус.

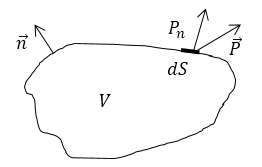
Поясним данную формулировку. Выделим внутри некоторой среды объем $V$, который ограничивает поверхность $S$ (рис.1). Допустим, что полная энергия, которая заключена внутри объема, равна $W$. Тогда можно записать:

где $P_n$ — нормальная составляющая вектора Умова — Пойнтинга. Интегрирование в (4) производят по всей замкнутой поверхности $S$. Положительным считают направление внешней нормали $overrightarrow$, что означает поток вектора $overrightarrow

$ (выражение, которое стоит в формуле (4) в правой части) считают большим нуля, если линии потока энергии $overrightarrow

$ выводят наружу из объема.

При этом $-frac$- величина, на которую уменьшатся, полная энергия внутри объема $V$ за единицу времени. По закону сохранения энергии она должна быть равна энергии, которая выходит через поверхность $S$ за единицу времени наружу. Следовательно, энергия, покидающая объем $V$ через поверхность $S$, выражена потоком вектора Умова — Пойнтинга.

Задание: Напишите выражение для вектора Умова — Пойнтинга, если энергию переносит волна, уравнение изменения вектора напряженности электрического поля которой задано как: $overrightarrow=10cosleft(omega t-kx+alpha right)overrightarrow(frac).$ Учесть, что амплитуда вектора напряженности магнитного поля имеет вид: $H_moverrightarrow$, частота волны $omega при ней varepsilon =2, mu approx 1 .$

Решение:

За основу решения задачи, примем определение вектора Умова — Пойнтинга:

Из условий видим, что колебания вектора напряженности электрического поля происходят по $оси Z$, колебания вектора напряженности магнитного поля по $оси X$, следовательно, вектор Умова — Пойнтинга колеблется по $оси Y$.

Модуль искомого вектора можно найти как:

Найдем амплитуду вектора $overrightarrow$, если знаем, что амплитудные значения в нашем случае связаны соотношением:

Выразим из (1.3) искомую амплитуду $H_m$, имеем:

При этом уравнение колебаний вектора напряженности запишем в виде:

Используя уравнения (1.1), (1.5) и уравнение колебаний вектора напряжённости электрического поля из условий задачи, запишем выражение для вектора Умова — Пойнтинга:

Ответ: $overrightarrow

=sqrt<frac<varepsilon _0><mu _0>>^2c^2left(omega t-kx+alpha right)overrightarrow.$

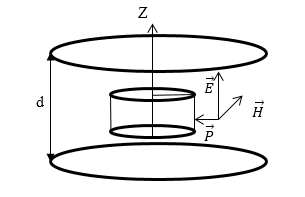
Задание: Плоский конденсатор, имеющий круглые обкладки заряжен постоянным током за время $t_0$ до напряжения $U$. Расстояние между пластинами конденсатора равно $d$. Запишите выражение для вектора Умова — Пойнтинга для точек воображаемой цилиндрической поверхности радиуса $r$, которая находится между обкладками конденсатора. Считайте, что радиус пластин конденсатора много больше, чем радиус воображаемого цилиндра.

Решение:

За основу решения задачи, примем определение вектора Умова — Пойнтинга:

Переменное электрическое поле, возникающее в результате разрядки конденсатора, вызывает переменное магнитное поле. Запишем уравнение из системы Максвелла, учитывая, что между обкладками конденсатора токов проводимости нет:

и материальное уравнение:

Возьмем производную от $overrightarrow$ по времени:

Возьмём интеграл от $rotoverrightarrow$ по поверхности цилиндра радиуса $r$, применим теорему Стокса:

Приравняем правые части выражений (2.6), (2.7), согласно тому, что выполняется (2.5):

Найдем модуль вектора Умова — Пойнтинга согласно выражениям (2.1) и (2.8):

Задание: Плоская электромагнитная волна распространяется в вакууме по $оси X$. Чему равна средняя энергия, которая проходит через единицу поверхности в единицу времени?

Решение:

сли мы имеем плоскую электромагнитную волну, то модули напряженности полей $overrightarrow $и $overrightarrow$ в произвольной точке $x$ могут быть выражены как:

где $k=frac$. Следовательно, мгновенное значение вектора $overrightarrow

$ можно записать в виде:

[P=E_0<H_0^2 left(omega t-kxright) >left(1.3right).]

По условию задачи волна распространяется в вакууме, следовательно, $varepsilon =1, mu =1 $, имеем следующее соотношение между амплитудами полей:

Кроме того, известно, что среднее значение $leftlangle ^2alpha rightrangle =frac,$ тогда используем (1.3), (1.4) получаем среднее значение вектора Умова — Пойнтинга ($leftlangle Prightrangle $) равно:

Ответ: Средняя энергия, которая проходит через единицу поверхности за единицу времени (интенсивность волны), равна $leftlangle Prightrangle =sqrt<frac<_0><_0>>frac.$

Задание: Вычислите среднее значение вектора Умова — Пойнтинга в стоячей волне.

Решение:

Колебания электрического и магнитного полей можно представить в стоячей волне с использованием следующих гармонических законов:

где $_E, varphi_H$- запаздывание по фазе отраженной волны соответствующего поля, то есть:

здесь $theta ,vartheta $ — изменение фазы при отражении, они равны или $pi , $или 0. $l-$длина линии (если рассматривается свободная волна, то это расстояние от излучателя до поверхности отражения). Обозначим:

тогда колебания, исходя из (2.1) и (2.2) в точке $x$ можно записать как:

при этом очевидно, что $E_1$ и $H_1$ не зависят от времени. Допустим, что $theta =pi $, тогда:

Исходя из (2.9) и (2.10), для вектора Умова — Пойнтинга получим:

Из формулы (2.11) следует, что колебания модуля вектора $overrightarrow

$ происходят с частотой $2omega $, при этом периодически изменяется знак. Следовательно, среднее значение вектора по времени равно $0$ ($leftlangle Prightrangle =0$).

Ответ: В стоячей волне течения энергии нет, $leftlangle Prightrangle =0$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 02 2022

🎥 Видео

Билет №38 "Поток энергии"Скачать

Основные физические понятия технической электродинамики, 1978Скачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Момент инерцииСкачать

Энергия течёт в пространстве а не в проводе Вектор Умова ПойтингаСкачать

Лекция 25: Закон сохранения энергии. Вектор Умова-Пойнтинга.Скачать

Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

ЭЛЕКТРОД тестирование, шестой семестрСкачать

Пожалуй, главное заблуждение об электричестве [Veritasium]Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

3.5 Комплексный вектор ПойнтингаСкачать

Движение плотности энергии протяженного электрона описывает вектор Умова, а не Пойтинга / С.В.БлиновСкачать