Дана теорема для того чтобы четырехугольник был параллелограммом (2 видео)

Задание 9. Отношения логического следования и равносильности

Задача 1. Дана теорема: «Для того чтобы диагонали четырехугольника в точке пересечения делились пополам, достаточно, чтобы этот четырехугольник был параллелограммом».

1. Переформулируйте данную теорему, используя слова «следует», «любой», «необходимо».

2. Сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.

Решение. Чтобы решить задачу, надо выделить условие и заключение данной теоремы. Для этого устанавливаем, к какому предложению в теореме относится слово «достаточно». Согласно определению оно и будет условием.

1. Условием теоремы является утверждение «четырехугольник – параллелограмм» (обозначим его через А). Утверждение «в четырехугольнике диагонали делятся пополам» является её заключением (обозначим его через В).

Используя принятые обозначения, можно представить теорему в виде: А 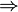В и прочитать так: «Из А следует В», «Любое А есть В», «В необходимо для А». В соответствии со сказанным получаем следующие формулировки данной теоремы:

· Из того, что четырехугольник – параллелограмм, следует, что его диагонали в точке пересечения делятся пополам.

· Во всяком параллелограмме диагонали в точке пересечения делятся пополам.

· Для того чтобы четырехугольник был параллелограммом, необходимо, чтобы диагонали этого четырехугольника в точке пересечения делились пополам.

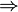
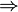
2. Согласно закону контрапозиции теорема вида А В равносильна теореме ˉВˉ ˉАˉ. Таким образом, получаем следующую формулировку: «Если диагонали четырехугольника не делятся в точке пересечения пополам, то этот четырехугольник не является параллелограммом».

Задача 2. Вместо многоточия вставить термины «необходимо», «достаточно», «необходимо и достаточно»:

1. Для того чтобы число х являлось делителем числа 15,……., чтобы число х являлось делителем числа 5.

2. Для того чтобы гражданин России имел право голоса,……. чтобы он достиг 18 лет.

Решение. Если истинно высказывание ( х)А(х) В(х), то А(х) называют достаточным условием для В(х). Если истинно высказывание

( х)В(х) А(х), то А(х) называют необходимым условием для В(х). Если истинны оба высказывания, то А(х) называют необходимым и достаточным условием для В(х).

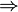
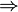
1. Введем обозначения: А(х) : число х является делителем числа 5; В(х): число х является делителем числа 15. Рассмотрим высказывание

( х)А(х) В(х) – любой делитель числа 5 является делителем числа 15. Высказывание истинно, значит А(х) – достаточное условие для В(х). Обратная импликация ( х)В(х) А(х) – любой делитель числа 15 является делителем числа 5 – ложно, поэтому А(х) не будет необходимым условием для В(х).

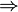
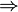
Вывод: для того чтобы число х являлось делителем числа 15, достаточно, чтобы число х являлось делителем числа 5.

2. Аналогично, пусть А(х): гражданин России х достиг 18 лет; В(х): гражданин России х имеет право голоса. Высказывание ( х)А(х) В(х) истинно, так как действительно, что любой гражданин России, достигший 18 лет, имеет право голоса. Поэтому А(х) – достаточное условие для В(х). Истинна и обратная импликация ( х)В(х) А(х). Если гражданин России имеет право голоса, то он достиг 18 лет. А(х) – необходимое условие для В(х).

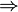
Вывод: для того чтобы гражданин России имел право голоса, необходимо и достаточно, чтобы он достиг 18 лет.

Содержание

ДОСТАТОЧНОЕ УСЛОВИЕ
Презентация по математике «НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ В МАТЕМАТИКЕ»
«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
📹 Видео

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

ДОСТАТОЧНОЕ УСЛОВИЕ

ДОСТАТОЧНОЕ УСЛОВИЕ для выполнения какого-либо верного утвержде ния (предложения, суждения) — всякое условие, из которого следует это утвер ждение. Например, для делимости целого многозначного числа на 4 достаточным условием является окончание этого числа по крайней мере двумя нулями. Но это условие — равенство двух последних цифр целого числа нулю — не является необходимым условием для делимости целого числа на 4. Однако можно указать такое условие делимости цедрго многозначного числа на 4, которое будет и необходимым и достаточным; это условие состоит в том, что двузначное число, на которое оканчивается многозначное число, должно делиться на 4. Действительно, если двузначное число, на которое оканчивается многозначное число, делится на 4, то и все многозначное число делится на 4, и обратно — верно, если многозначное число делится на 4, то и двузначное число, на которое оно оканчивается, делится на 4.
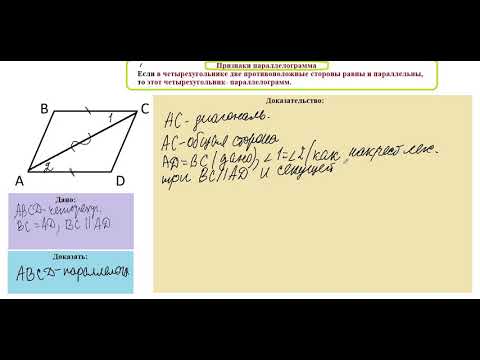
Достаточное условие является одним из важнейших понятий математики и часто встречается в формулировках теорем наряду с необходимым условием. Достаточное условие называется также достаточным признаком для выполнения какого-либо верного утверждения. Для выполнения какого-либо утверждения можно указать не один, а несколько достаточных условий. Например, для того чтобы выпуклый четырехугольник был параллелограммом, достаточно одного из условий: 1) чтобы любые две его противоположные стороны были равны и параллельны друг другу; 2) чтобы в точке пересечения его диагонали делились пополам; 3) чтобы этот четырехугольник имел центр симметрии. См. также Необходимое условие, Критерий, Теорема.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Презентация по математике «НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ В МАТЕМАТИКЕ»

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Параллелограмм. 8 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

УРОК ПО ТЕМЕ: «НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ В МАТЕМАТИКЕ» Класс: 9, 10, 11. Учитель: Абузов Юрий Иванович. Стаж: 42 года. Категория: высшая. Школа: МБОУ СОШ п. Селекция, Кстовского района, Нижегородской области. Дата: январь 2015 года.

Некоторые комментарии. В программе по математике средней школы, где математики в 10-11 классах 4 часа в неделю, а в 5-9 классах 5 часов в неделю нет темы «Необходимые и достаточные условия». Тем не менее, в задачах и теоремах встречаются слова «необходимо и достаточно», «тогда и только тогда», «в том и только в том случае». Определенные трудности испытывают и выпускники школ, когда на лекциях по математике в вузах слышат слова «необходимо и достаточно». Данная тема довольно сложная, вся трудность заключается в ее логическом смысле. Неплохо, если учитель в своей речи уже с пятого класса использует эти слова, не объясняя ученикам их логического смысла. В связи с этим полезно провести уроки на эту тему (на элективе, факультативе, кружке). Включить учащихся в деятельность по открытию необходимых и достаточных условий учитель может только ведя их за собой, показывая образец рассуждений.

Конспект урока. Тема урока. Необходимые и достаточные условия в математике. Тип урока. Урок изучения нового учебного материала. Цель урока. Учащиеся должны знать Необходимые и Достаточные условия и применять их при доказательстве теорем и решении задач.

Структура урока. Актуализация знаний. Введение Необходимых и Достаточных условий. Узнавание Необходимых и Достаточных условий в примерах. Решение задач на Необходимые и Достаточные условия. Подведение итогов. Выдача домашнего задания и его комментирование.

Актуализация. Каждая теорема содержит условие и заключение. Правда, эти части теоремы не всегда бывают отчетливо выделены. Например: диагонали ромба взаимно перпендикулярны. Очень важно уметь выделять условия и заключения, т.е. представить теорему в виде: Если А (условие), то В (заключение). В нашем примере: Если четырехугольник ромб, то его диагонали взаимно перпендикулярны. Выделите в следующих теоремах условие и заключение: Вертикальные углы равны В прямоугольнике диагонали равны Синусы равных углов равны Косинусы смежных углов отличаются только знаком Разность двух чисел, умноженная на их сумму, равна разности квадратов этих чисел Сумма смежных углов равна 180 градусов Параллелограмм имеет центр симметрии Повторить признаки и свойства параллелограмма.

Определение: В истинной теореме её заключение называют необходимым условием её условия. Сформулируем эту теорему, применяя слово «необходимо»: центральная симметрия необходима для параллелограмма наличие центра симметрии – необходимое условие параллелограмма. Далее идут упражнения на отыскание Необходимых Условий. Можно их приготовить на плакате, кодопленках, компьютере.

Найдите Необходимые Условия параллелограмма АВСД: Методика выполнения такая: составь теорему установи, истинна она или нет если истинна, то соответствующее заключение есть Необходимые Условия параллелограмма. Если теорема ложная, то заключение не является Необходимым Условием. М – центр симметрии СД = АВ ВД = АС ∠ А= ∠ В ∠ А= ∠ С Δ АВС= Δ АДС ∠ А= ∠ Д ∠ А+ ∠ Д=180° МА = МС, МВ = МД

Рассмотрим «Достаточные условия».

Формулировка Определение: В верной теореме её условие называется Достаточным Условием её заключения. Сформулируем эту теорему, используя слово «достаточно»: вертикальность углов достаточна для их равенства чтобы углы были равны, достаточно их вертикальности.

Свойства и признаки параллелограмма. Если четырёхугольник – параллелограмм, то Четырёхугольник – параллелограмм, если противоположные стороны попарно равны противоположные углы попарно равны диагонали точкой пересечения делятся пополам две противоположные стороны равны и параллельны

Теорема о диагоналях параллелограмма. Сформулируем теорему о диагоналях параллелограмма. Для того, чтобы четырехугольник был параллелограммом, необходимо и достаточно, чтобы его диагонали, пересекаясь, точкой пересечения делились пополам. Часто вместо слов «необходимо и достаточно» употребляют другие, например, «тогда и только тогда», «в том и только в том случае».

8. Непрерывность есть … условие дифференцируемости. Ответ: Н 9. Дифференцируемость функции — … условие непрерывности. Ответ: Д 10. Для делимости суммы «а + в» на 3, … чтобы каждое слагаемое делилось на 3. Ответ: Д 11. Чтобы треугольник был прямоугольным, … чтобы квадрат большей стороны был бы равен сумме квадратов двух других его сторон. Ответ: Н и Д 12. Третий признак равенства треугольников есть … условие равенства треугольников. Ответ: Н и Д 13. Равенство производной в точке нулю или её не существование в точке есть … условие экстремума функции. Ответ: Н 14. Центр симметрии есть … условие параллелограмма. Ответ: Н и Д

Упражнения на доказательство

Подведение итогов урока. Выдача домашнего задания и его комментирование.

Рассмотрим решение некоторых заданий.

Заполнить пропуски словами: «необходимо, но недостаточно», «достаточно, но не необходимо», «необходимо и достаточно», «не необходимо и недостаточно». 1. Для того, чтобы треугольник был равнобедренным, … , чтобы одна из его высот была медианой Ответ: Н и Д 2. Чтобы четырехугольник был параллелограммом, … , чтобы какие-нибудь два угла его составляли в сумме 180 градусов Ответ: Н, но не Д 3. Чтобы четырехугольник был параллелограммом, … , чтобы он имел три прямых угла Ответ: Д, но не Н 4. Чтобы данная точка являлась центром вписанной в треугольник окружности, … , чтобы она лежала на одной из биссектрис углов треугольника Ответ: не Н и не Д 5. Для того, чтобы два ненулевых вектора были перпендикулярны, … , чтобы их скалярное произведение было равно нулю Ответ: Н и Д 6. Чтобы один из углов треугольника был равен 30 градусов, … , чтобы длина одной из сторон была равна половине другой стороны Ответ: не Н и не Д 7. Чтобы около четырехугольника можно было описать окружность, … , чтобы он был равнобедренной трапецией Ответ: Д, но не Н Алгоритм выполнения упражнений: Составь теорему Составь теорему, обратную данной Проверь их на истинность Выбери нужные слова Сформулируй ответ