Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
- Согласованные матрицы
- Определение умножения
- Умножение квадратных матриц
- Основные свойства матричного произведения
- Случай прямоугольных матриц
- Вектор-строки и вектор-столбцы
- Возведение матрицы в степень
- Как находить произведение матриц. Умножение матриц. Скалярное произведение матриц. Произведение трех матриц
- Матрица и число
- Векторы и условие существования произведения матриц
- Умножение на вектор-столбец
- Умножение вектор-строки на матрицу
- Произведение прямоугольных матриц
- Умножение трех матриц: теоретическая часть
- Умножение трех матриц: практика
- Знакомство с прямым произведением
- Определитель произведения
- Ранг произведения
- Знакомство с матрицами
- Что такое матрица
- Простые операции с матрицами
- Сложение и вычитание матриц
- Умножение матриц
- Что дальше
Видео:Вектор-строка / Вектор-столбец / Ориентация вектора: Линейная алгебра для Data Science #datascienceСкачать
Согласованные матрицы
Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=left[ mtimes n right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.
Определение. Матрицы вида $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, в которых количество столбцов в первой матрице совпадает с количеством строк во второй, называются .
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
- Нам важен порядок матриц. Например, матрицы $A=left[ 3times 2 right]$ и $B=left[ 2times 5 right]$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=left[ 2times 5 right]$ и $A=left[ 3times 2 right]$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
- Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.
Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $left[ ntimes n right]$ согласованы всегда.
В математике, когда важен порядок перечисления объектов (например, в рассмотренном выше определении важен порядок матриц), часто говорят об упорядоченных парах. Мы встречались с ними ещё в школе: думаю, и ежу понятно, что координаты $left( 1;0 right)$ и $left( 0;1 right)$ задают разные точки на плоскости.
Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $left( A;B right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй».
Ну и что с того?
Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать
Определение умножения
Рассмотрим две согласованные матрицы: $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$. И определим для них операцию умножения.
Определение. $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой считаются по формуле:
Обозначается такое произведение стандартно: $C=Acdot B$.
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
- Что это за лютая дичь?
- А почему так сложно?
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
Прежде всего заметим, что длинная строчка для расчёта $<_>$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:
- Берём $i$-ю строку в первой матрице;
- Берём $j$-й столбец во второй матрице;
- Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.
Данный процесс легко понять по картинке:
Схема перемножения двух матриц
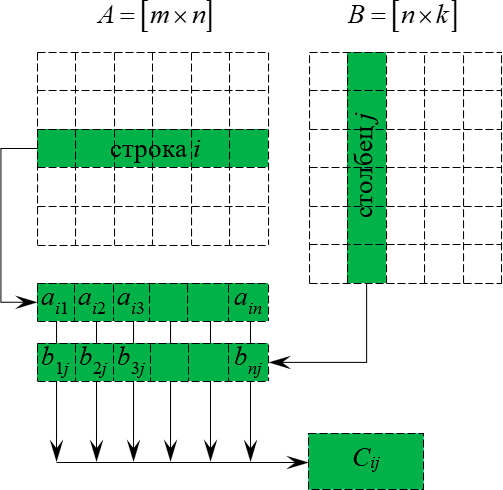
Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем $<_>$. И так для всех $1le ile m$ и $1le jle k$. Т.е. всего будет $mtimes k$ таких «извращений».
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
Тогда их скалярным произведением будет именно сумма попарных произведений:
По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $overrightarrow$ на вектор-столбец $overrightarrow$.
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Видео:Работа с массивами. Вектор столбцы и вектор строки 2. Урок 8Скачать
Умножение квадратных матриц
[left[ begin<*> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*> -2 & 4 \ 3 & 1 \end right]]
Решение. Итак, у нас две матрицы: $A=left[ 2times 2 right]$ и $B=left[ 2times 2 right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение:
[begin & left[ begin<*> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*> -2 & 4 \ 3 & 1 \end right]=left[ begin<*> 1cdot left( -2 right)+2cdot 3 & 1cdot 4+2cdot 1 \ -3cdot left( -2 right)+4cdot 3 & -3cdot 4+4cdot 1 \end right]= \ & =left[ begin<*> 4 & 6 \ 18 & -8 \end right]. end]
Задача 2. Выполните умножение:
[left[ begin 1 & 3 \ 2 & 6 \end right]cdot left[ begin<*>9 & 6 \ -3 & -2 \end right]]
Решение. Опять согласованные матрицы, поэтому выполняем действия:[]
[begin & left[ begin 1 & 3 \ 2 & 6 \end right]cdot left[ begin<*> 9 & 6 \ -3 & -2 \end right]=left[ begin<*> 1cdot 9+3cdot left( -3 right) & 1cdot 6+3cdot left( -2 right) \ 2cdot 9+6cdot left( -3 right) & 2cdot 6+6cdot left( -2 right) \end right]= \ & =left[ begin 0 & 0 \ 0 & 0 \end right]. end]
Как видим, получилась матрица, заполненная нулями
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Видео:Умножение матрицСкачать
Основные свойства матричного произведения
В двух словах. Умножение матриц:
- Некоммутативно: $Acdot Bne Bcdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $Acdot B=Bcdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
- Ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
- Дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$ и $left( A+B right)cdot C=Acdot C+Bcdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
[left[ begin<*> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*> -2 & 4 \ 3 & 1 \end right]=left[ begin<*>4 & 6 \ 18 & -8 \end right]]
Но если поменять матрицы местами, то получим совсем другой результат:
[left[ begin<*> -2 & 4 \ 3 & 1 \end right]cdot left[ begin<*> 1 & 2 \ -3 & 4 \end right]=left[ begin -14 & 4 \ 0 & 10 \end right]]
Получается, что $Acdot Bne Bcdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $left[ 2times 3 right]$ и $left[ 3times 5 right]$ вполне себе согласованы в указанном порядке, но те же матрицы $left[ 3times 5 right]$ и $left[ 2times 3 right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(
Среди квадратных матриц заданного размера $n$ всегда найдутся такие, которые дают одинаковый результат как при перемножении в прямом, так и в обратном порядке. Как описать все подобные матрицы (и сколько их вообще) — тема для отдельного урока. Сегодня не будем об этом.:)
Тем не менее, умножение матриц ассоциативно:
[left( Acdot B right)cdot C=Acdot left( Bcdot C right)]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $left[ ntimes n right]$. Множество всех таких матриц обозначается $<^>$ (т.е. записи $A=left[ ntimes n right]$ и [Ain <^>] означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.
Определение. размера $n$ — это такая матрица $E$, что для любой квадратной матрицы $A=left[ ntimes n right]$ выполняется равенство:
[Acdot E=Ecdot A=A]
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Видео:4. Умножение матриц, примеры с решениемСкачать
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
[left[ begin begin 5 \ 2 \ 3 \end & begin 4 \ 5 \ 1 \end \end right]cdot left[ begin<*> -2 & 5 \ 3 & 4 \end right]]
Решение. Имеем две матрицы: $A=left[ 3times 2 right]$ и $B=left[ 2times 2 right]$. Выпишем числа, обозначающие размеры, в ряд:
Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=left[ 3times 2 right]$:
[begin & left[ begin begin 5 \ 2 \ 3 \end & begin 4 \ 5 \ 1 \end \end right]cdot left[ begin<*> -2 & 5 \ 3 & 4 \end right]=left[ begin<*> 5cdot left( -2 right)+4cdot 3 & 5cdot 5+4cdot 4 \ 2cdot left( -2 right)+5cdot 3 & 2cdot 5+5cdot 4 \ 3cdot left( -2 right)+1cdot 3 & 3cdot 5+1cdot 4 \end right]= \ & =left[ begin<*> 2 & 41 \ 11 & 30 \ -3 & 19 \end right]. end]
Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=left[ 3times 2 right]$.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
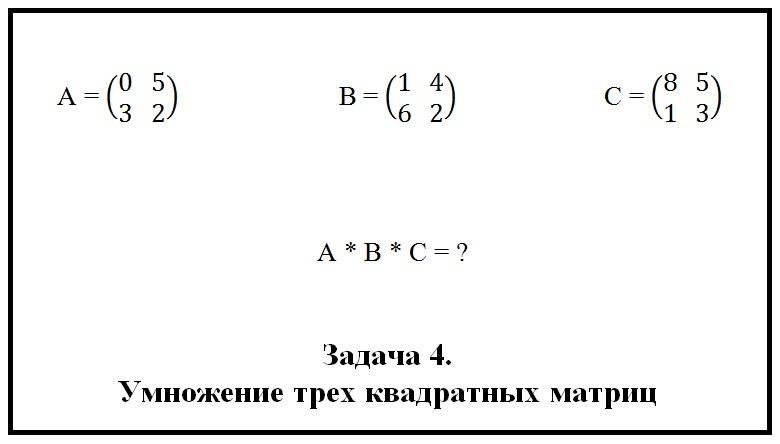
Задача 4. Найдите все возможные попарные произведения матриц:
Решение. Для начала запишем размеры матриц:
[A=left[ 2times 4 right]; B=left[ 4times 2 right]; C=left[ 2times 2 right]]
Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение:
[Acdot B=left[ begin<*> 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end right]cdot left[ begin<*> 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end right]=left[ begin<*>-10 & 7 \ 10 & 7 \end right]]
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
[A cdot B=left[ 2times 4 right]cdot left[ 4times 2 right]=left[ 2times 2 right]]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
Какие ещё возможны варианты? Безусловно, можно найти $Bcdot A$, поскольку $B=left[ 4times 2 right]$, $A=left[ 2times 4 right]$, поэтому упорядоченная пара $left( B;A right)$ является согласованной, а размерность произведения будет:
[B cdot A=left[ 4times 2 right]cdot left[ 2times 4 right]=left[ 4times 4 right]]
Короче говоря, на выходе будет матрица $left[ 4times 4 right]$, коэффициенты которой легко считаются:
[Bcdot A=left[ begin<*> 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end right]cdot left[ begin<*> 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end right]=left[ begin<*>1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end right]]
Очевидно, можно согласовать ещё $Ccdot A$ и $Bcdot C$ — и всё. Поэтому просто запишем полученные произведения:
[Ccdot A=left[ begin<*> 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end right]]
[Bcdot C=left[ begin<*>1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end right]]
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Определение. — это матрица размера $left[ mtimes 1 right]$, т.е. состоящая из нескольких строк и только одного столбца.
— это матрица размера $left[ 1times n right]$, т.е. состоящая из одной строки и нескольких столбцов.
[left[ begin<*> 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end right]cdot left[ begin<*> 1 \ 2 \ -1 \end right]]
Решение. Перед нами произведение согласованных матриц: $left[ 3times 3 right]cdot left[ 3times 1 right]=left[ 3times 1 right]$. Найдём это произведение:
[left[ begin<*> 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end right]cdot left[ begin<*> 1 \ 2 \ -1 \end right]=left[ begin<*> 2cdot 1+left( -1 right)cdot 2+3cdot left( -1 right) \ 4cdot 1+2cdot 2+0cdot 2 \ -1cdot 1+1cdot 2+1cdot left( -1 right) \end right]=left[ begin<*> -3 \ 8 \ 0 \end right]]
Задача 6. Выполните умножение:
[left[ begin<*> 1 & 2 & -3 \end right]cdot left[ begin<*> 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end right]]
Решение. Опять всё согласовано: $left[ 1times 3 right]cdot left[ 3times 3 right]=left[ 1times 3 right]$. Считаем произведение:
[left[ begin<*> 1 & 2 & -3 \end right]cdot left[ begin<*> 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end right]=left[ begin<*>5 & -19 & 5 \end right]]
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Видео:Матрицы и векторыСкачать
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
[Acdot A=left[ ntimes n right]cdot left[ ntimes n right]=left[ ntimes n right]]
И обозначаются точно так же, как и обычные степени:
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
[begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^>=left[ begin 1 & 1 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*> 1cdot 1+1cdot 0 & 1cdot 1+1cdot 1 \ 0cdot 1+1cdot 0 & 0cdot 1+1cdot 1 \end right]= \ & =left[ begin<*> 1 & 2 \ 0 & 1 \end right] end]
[begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^>= <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*> 1 & 2 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*> 1 & 3 \ 0 & 1 \end right] end]
Ответ: $left[ begin1 & 3 \ 0 & 1 \end right]$.
Задача 8. Возведите матрицу в указанную степень:
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
[begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^>= <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left( left[ begin 1 & 3 \ 0 & 1 \end right]cdot left[ begin 1 & 3 \ 0 & 1 \end right] right)cdot left( left[ begin 1 & 3 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right] right)= \ & =left[ begin 1 & 6 \ 0 & 1 \end right]cdot left[ begin 1 & 4 \ 0 & 1 \end right]= \ & =left[ begin 1 & 10 \ 0 & 1 \end right] end]
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $left[ 3times 3 right]$.
Задача 9. Возведите матрицу в указанную степень:
Решение. Не будем искать закономерности. Работаем «напролом»:
[ <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>= <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>cdot left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]]
Для начала возведём эту матрицу в квадрат:
[begin & <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>=left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]cdot left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]= \ & =left[ begin<*> 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end right] end]
Теперь возведём в куб:
[begin & <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>=left[ begin<*> 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end right]cdot left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]= \ & =left[ begin<*> 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end right] end]
Вот и всё. Задача решена.
Ответ: $left[ begin 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end right]$.
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
Видео:Основы МАТЛАБ.РАБОТА С МАССИВАМИ. ВЕКТОРЫ-СТОЛБЦЫ И ВЕКТОРЫ-СТРОКИСкачать
Как находить произведение матриц. Умножение матриц. Скалярное произведение матриц. Произведение трех матриц
С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.
Видео:Линал 2.6. Умножение матрицы на векторСкачать
Матрица и число
Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами aij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами bij, которые находятся по формуле:
Вам будет интересно: Обомлеть — это что значит? Определение и синонимы
Т. е. для получения элемента b11 нужно взять элемент a11 и умножить его на нужное число, для получения b12 требуется найти произведение элемента a12 и числа e и т. д.
Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:
Таким образом, мы получили прямоугольный массив с числовыми элементами.
| 18 | –6 | 12 |
| 15 | 9 | –3 |
Видео:numpy01 - Вектор строки и вектор столбцы#shortsСкачать
Векторы и условие существования произведения матриц
Вам будет интересно: «Неожиданный» — это какой? Значение слова
В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a1 до an. Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.
Векторы можно называть матрицами:
- вектор-столбец – это матрица, построенная из одного столбца;
- вектор-строчка – это матрица, которая включает в себя только одну строку.
При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.
При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.
Видео:Умножение матрицСкачать
Умножение на вектор-столбец
Вам будет интересно: Инженерия знаний. Искусственный интеллект. Машинное обучение
При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.
Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:
y1 = a11x1 + a12x2 + … + a1nxn,
y2 = a21x1 + a22x2 + … + a2nxn,
ym = am1x1 + am2x2 + … + amnxn,
где x1, …, xn – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a11, a12, …, amn – элементы матрицы A.
Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.
Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:
Видео:Векторное произведение векторов | Высшая математикаСкачать
Умножение вектор-строки на матрицу
Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно. Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.
Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:
yk = a1kx1 + a2kx2 + … + amkxm,
где yk – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать
Произведение прямоугольных матриц
Это вычислительное действие может показаться сложным. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.
Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов cij:
Вам будет интересно: Изотоп лития: определение и применение
Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.
| 16 | 12 | 9 |
| 31 | 18 | 36 |
Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать
Умножение трех матриц: теоретическая часть
Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:
Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна. Должны существовать произведения A × B и B × C.
Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).
Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать
Умножение трех матриц: практика
Квадратные матрицы
Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.
Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.
Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:
- d11 = 0 × 1 + 5 × 6 = 30;
- d12 = 0 × 4 + 5 × 2 = 10;
- d21 = 3 × 1 + 2 × 6 = 15;
- d22 = 3 × 4 + 2 × 2 = 16.
Промежуточный результат готов.
| 30 | 10 |
| 15 | 16 |
Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:
- g11 = 30 × 8 + 10 × 1 = 250;
- g12 = 30 × 5 + 10 × 3 = 180;
- g21 = 15 × 8 + 16 × 1 = 136;
- g22 = 15 × 5 + 16 × 3 = 123.
Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.
| 250 | 180 |
| 136 | 123 |
Прямоугольные матрицы
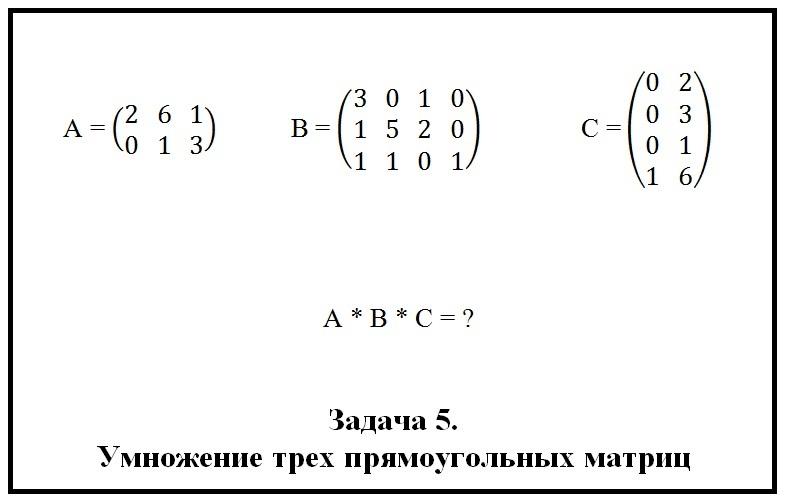
Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.
Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение. Приступим к решению задачи.
Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:
- d11 = 3 × 0 + 0 × 0 + 1 × 0 + 0 × 1 = 0;
- d12 = 3 × 2 + 0 × 3 + 1 × 1 + 0 × 6 = 7.
Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d21, d22, d31 и d32. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.
| 0 | 7 |
| 0 | 19 |
| 1 | 11 |
Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:
- f11 = 2 × 0 + 6 × 0 + 1 × 1 = 1;
- f12 = 2 × 7 + 6 × 19 + 1 × 11 = 139;
- f21 = 0 × 0 + 1 × 0 + 3 × 1 = 3;
- f22 = 0 × 7 + 1 × 19 + 3 × 11 = 52.
Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.
| 1 | 139 |
| 3 | 52 |
Видео:Собственные значения и собственные векторы матрицы (4)Скачать
Знакомство с прямым произведением
Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.
У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.
Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок. Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.
Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a11, во втором – на a12, в третьем – на a21, в четвертом – на a22.
Видео:МатрицыСкачать
Определитель произведения
При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц». Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.
Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:
det A = a11 × a22 – a12 × a21.
Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a11 = 2, a12 = 3, a21 = 5 и a22 = 1. Для вычисления определителя воспользуемся формулой:
det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.
У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:
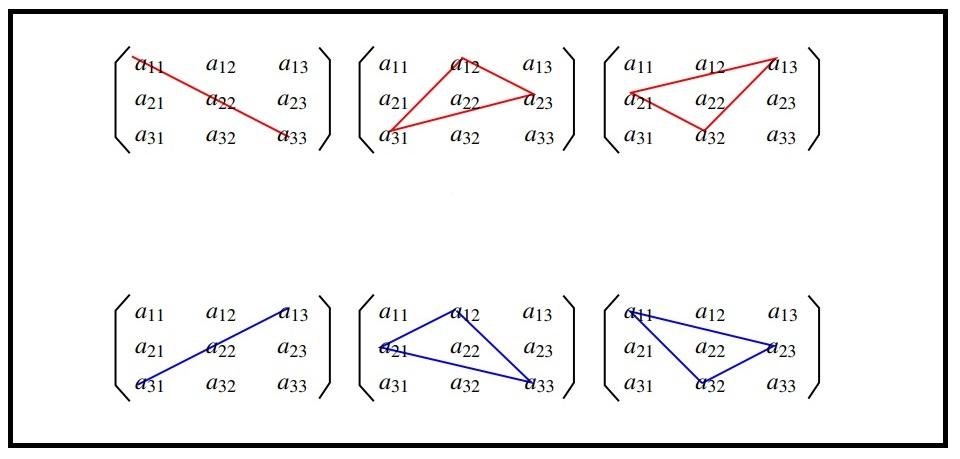
det A = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33.
Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.
Вам будет интересно: Погранвойска СССР: знаки отличия, функции, структура
Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и матрица B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.
Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1. Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.
Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:
- c11 = 2 × 4 + 3 × 1 = 11;
- c12 = 2 × 5 + 3 × 2 = 16;
- c21 = 1 × 4 + 1 × 1 = 5;
- c22 = 1 × 5 + 1 × 2 = 7.
Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.
Видео:Собственные векторы и собственные значения матрицыСкачать
Ранг произведения
Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:
- перестановку местами двух параллельно лежащих рядов;
- умножение всех элементов определенного ряда из таблицы на число, не равняющееся нулю;
- прибавление к элементам одного ряда элементов из другого ряда, умноженных на конкретное число.
После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.
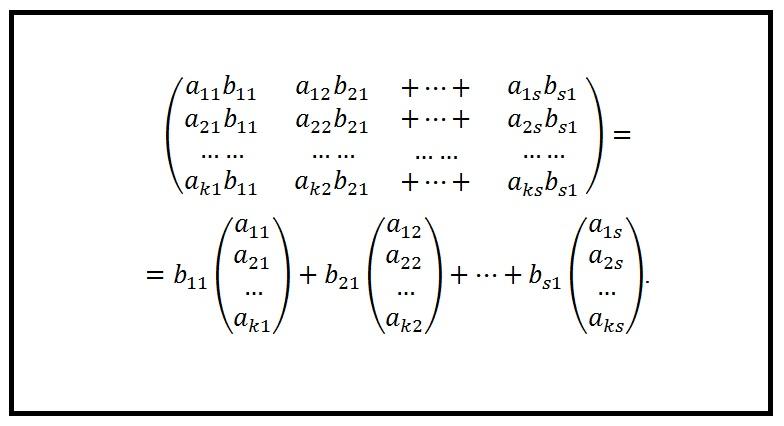
Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.
Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись. Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).
Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.
Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать
Знакомство с матрицами
Понятие и базовые операции.
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
- Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного.
- У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
- Векторы можно складывать, вычитать, умножать. Это чуть сложнее, чем с обычными числами.
- У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.
Общая схема матрицы 
Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три
Видео:Собственные значения и собственные векторыСкачать
Простые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.
Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре 
Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений
Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.
Пример умножения матрицы на число
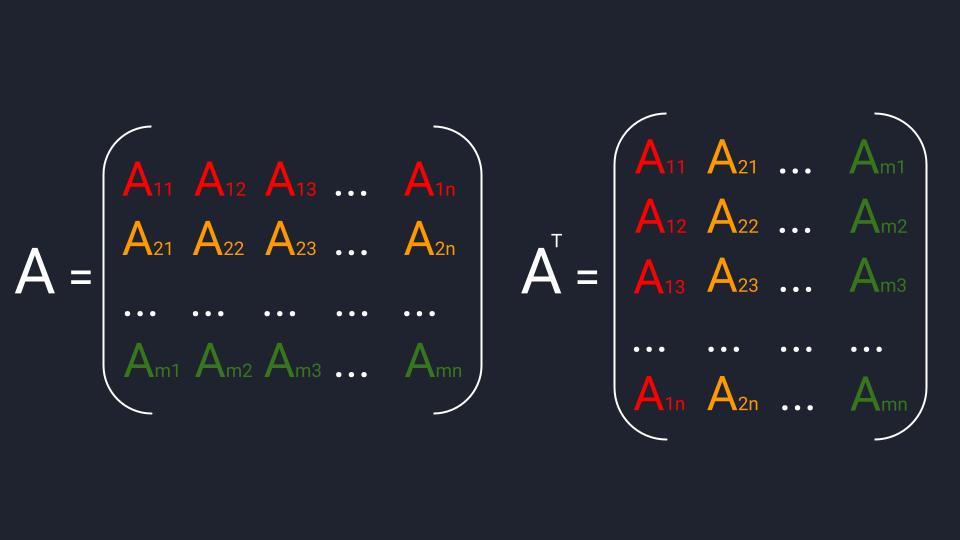
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.
Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы 
Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» 
Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил
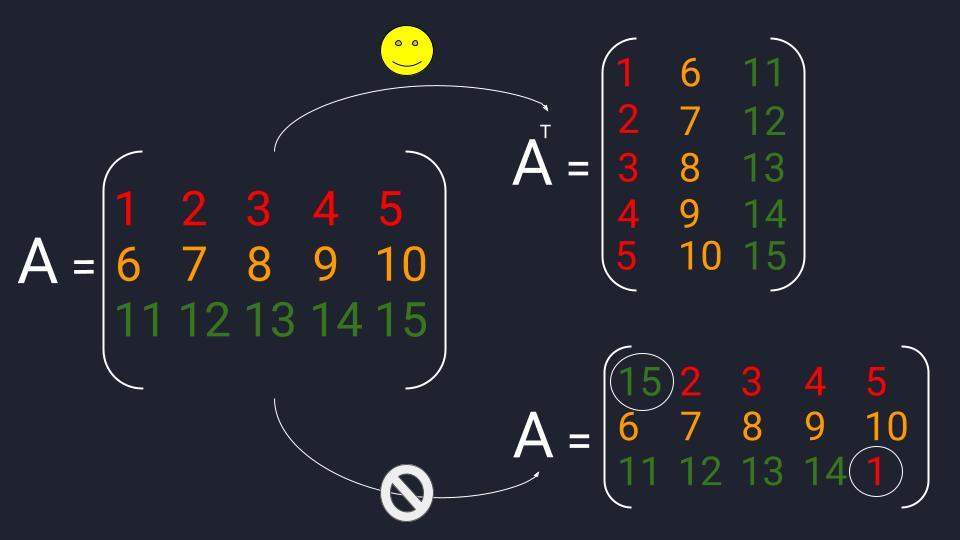
Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.
Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами 
Пример вычитания двух матриц
Умножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
- У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C.
- Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂.
- У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂.
- У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂.
- Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁).
- Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂).
- Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁).
- Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂).
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
Формула умножения матриц 
Пример умножения квадратных матриц размерностью 2×2
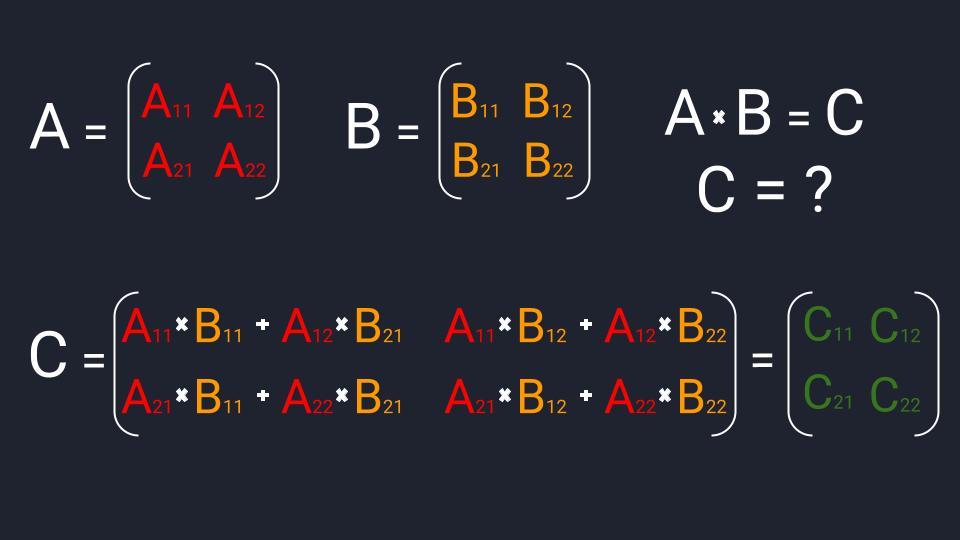
Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽