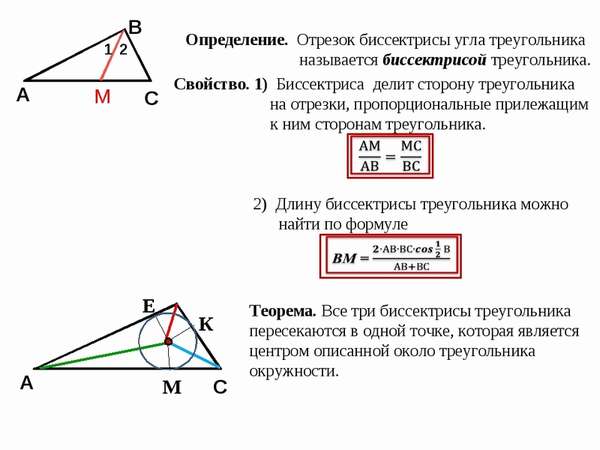
Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?
(свойство биссектрисы равностороннего треугольника)
В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
Проведем биссектрису BF.
По свойству равнобедренного треугольника, BF является также его медианой и высотой.
Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.
Что и требовалось доказать .
(свойство биссектрис равностороннего треугольника)
Все три биссектрисы равностороннего треугольника равны между собой.

AK, BF CD — биссектрисы треугольника ABC.
В треугольниках ABF, BCD и CAK:
- AB=BC=CA (по условию)
- ∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
- ∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).
Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.
Что и требовалось доказать .
Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.
1) Найдём биссектрису равностороннего треугольника через его сторону.

BF — биссектриса, BF=l.
По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.
Из прямоугольного треугольника ABF по определению синуса
Таким образом, формула биссектрисы равностороннего треугольника по его стороне:
2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.
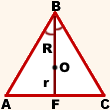
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.
Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.
Таким образом, длина биссектрисы через радиус вписанной окружности равна
- Свойства биссектрисы равностороннего треугольника
- Свойства биссектрисы равностороннего треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
- Пример задачи
- Вычисление биссектрисы треугольника с известными свойствами
- Свойства
- Свойства в равнобедренных треугольниках
- Определение биссектрисы треугольника
- Определение длины
- Нахождение величины угла
- 💥 Видео
Видео:Построение биссектрисы в треугольникеСкачать

Свойства биссектрисы равностороннего треугольника
В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.
Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.
Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Свойства биссектрисы равностороннего треугольника
Свойство 1
Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.
BD – биссектриса угла ABC, которая также является:
- высотой, опущенной на сторону AC;
- медианой, делящей сторону AC на два равных отрезка (AD = DC);
Свойство 2
Все три биссектрисы равностороннего треугольника равны между собой.
Свойство 3
Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
Свойство 4
Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.
- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r.
Свойство 5
Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.
Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.
Свойство 6
Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.
- AD и AE – внешние биссектрисы, параллельные BC;
- BK и BL – внешние биссектрисы, параллельные AC;
- CM и CN – внешние биссектрисы, параллельные AB.
Свойство 7
Длину биссектрисы ( la ) равностороннего треугольника можно выразить через его сторону.
где a – сторона треугольника.
Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Пример задачи
Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.
Решение
Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).
Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Вычисление биссектрисы треугольника с известными свойствами

- Свойства
- Свойства в равнобедренных треугольниках
- Определение биссектрисы треугольника
- Определение длины
- Нахождение величины угла
Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.
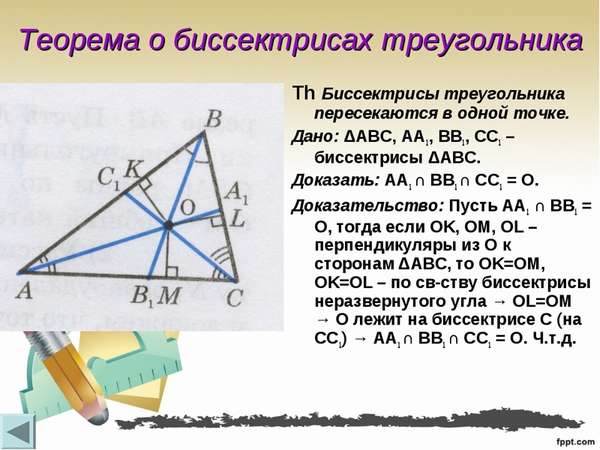
Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.
Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.
Это интересно: Как найти периметр треугольника.
Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Свойства
- Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
- Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.
Свойства в равнобедренных треугольниках
Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
- Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
- Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
- Все биссектрисы равностороннего треугольника обладают равенством.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение биссектрисы треугольника
Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.
Определение длины
Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

- Из свойств известно, что BD/CD = AB/AC.
- Значит, BD/CD = 5/4 = 1,25.
- BD/3 = 5/4.
- Значит, BD = 3,75.
- ABxAC = 54=20.
- CDxBD = 33,75 = 11,25.
Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.
Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.
Это интересно: в чем выражается эволюционный характер развития общества?
Нахождение величины угла
Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.
Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.
Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.
Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.
Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.
Биссектриса треугольника 


💥 Видео
Найдите биссектрису прямоугольного треугольника с катетами 3 и 5 ★ Как решать?Скачать

Свойство биссектрисы треугольника с доказательствомСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Задание 9 ОГЭ от ФИПИСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

ОГЭ 16🔴Скачать

Построение биссектрисы угла. 7 класс.Скачать

№488. Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см;Скачать

Формула для биссектрисы треугольникаСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Построение медианы в треугольникеСкачать

Задача найти сторону равностороннего треугольника по медианеСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

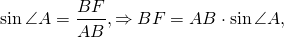
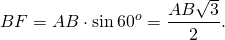
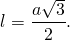
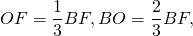
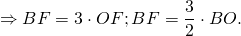







 Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.