Вектор силы в рычаг (8 видео) | Курс школьной геометрии

Правило рычага. Формулировка и формула

Рычаг представляет собой один из простых механизмов, который служил и продолжает служить людям для облегчения их физического труда. В статье рассмотрим, что такое рычаг, какие виды его бывают и где они применяются, а также поясним, в чем заключается правило рычага.

Содержание

Рычаг в физике
Когда человечество начало использовать рычаг?
Понятие о моменте силы
Моменты сил и правило рычага
Выигрыш и проигрыш в использовании рычага
Виды рычагов
Простой механизм блок
Решение задачи
Вектор силы в рычаг
Рычаг. Равновесие сил на рычаге
Содержание
Устройство рычага
Условие равновесия рычага
Примеры задач
🌟 Видео

Видео:Вектор нагрузки при приседаниях. Рычаг, плечо силы на рычаг.Скачать

Рычаг в физике

Несмотря на то что речь идет о простом механизме, он все же имеет свои составные части. Во-первых, это балка или доска, которая предназначена для воздействия на нее двух противоположных сил. Во-вторых, это опора, которая, с геометрической точки зрения, представляет собой ось вращения, вокруг которой может двигаться балка. В зависимости от расположения опоры под балкой различают три типа рычага, которые будут рассмотрены ниже.

Еще одним важным понятием для любого рычага является «плечо». Под ним понимают часть балки, которая находится между ее концом и опорой при условии, что воздействующие силы приложены к концам балки. Длина плеча играет важную роль при определении условий равновесия рычага.

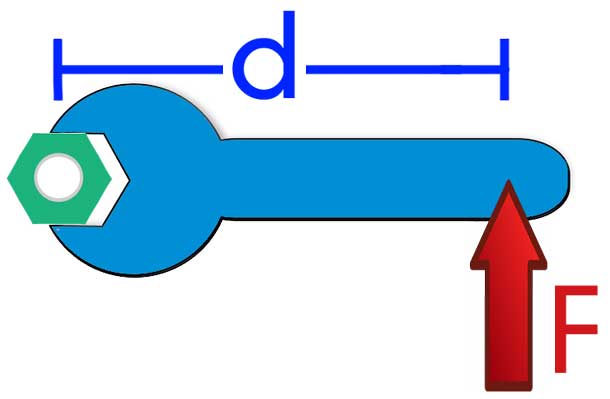
Рычаг предназначен для преобразования силы в перемещение или, наоборот, перемещения в силу. Другими словами, рассматриваемый простой механизм, используется для перераспределения работы, которую следует выполнить, в пользу приложенной силы или в пользу осуществляемого перемещения. Рисунок ниже показывает пример рычага первого рода.

Видео:Момент силыСкачать

Когда человечество начало использовать рычаг?

Ответить уверенно на этот вопрос нельзя. Известно, что рычаги с древнейших времен использовались в Месопотамии и Древнем Египте для подъема тар с водой из колодцев и рек.

Единственным письменным свидетельством, которое сохранилось до наших дней, свидетельствующим об использовании рассматриваемого механизма, является всем известный рычаг Архимеда. В работе Плутарха «Параллельные жизни» (100 год до н. э.) говорится, что Архимед в одиночку смог поднять корабль с грузом и пассажирами над поверхностью воды. При этом философ использовал систему блоков и рычагов.

Если подойти к поставленному в названии пункта вопросу более строго, то можно сказать, что человек пользуется рычагом с момента собственного появления в этом мире, ведь наши предплечья и плечи работают по принципу этого простого механизма.

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Понятие о моменте силы

Прежде чем переходить к формулировке правила равновесия рычага, рассмотрим понятие крутящего момента или момента силы. В физике под ним понимают величину, равную произведению плеча силы на саму силу. Математически это записывается так:

Где, F — воздействующая сила, d — плечо силы, которое соответствует расстоянию от точки приложения F до оси вращения. Последний элемент системы, то есть ось вращения, играет принципиальную роль при определении момента M. Без наличия оси вращения нет никакого смысла говорить о действующем моменте силы.

Физический смысл величины M заключается в отражении способности силы F совершить поворот системы вокруг оси. На практике эту способность можно ощутить, если попытаться открутить гайку не гаечным ключом, а руками, или же если постараться открыть дверь не за ручку, а толкая ее вблизи навесных петель.

Во время решения задач момент силы M может приводить как к вращению системы по часовой стрелке, так и против ее хода. В первой случае момент считают отрицательным, во втором — положительным.

Видео:Закон рычагаСкачать

Моменты сил и правило рычага

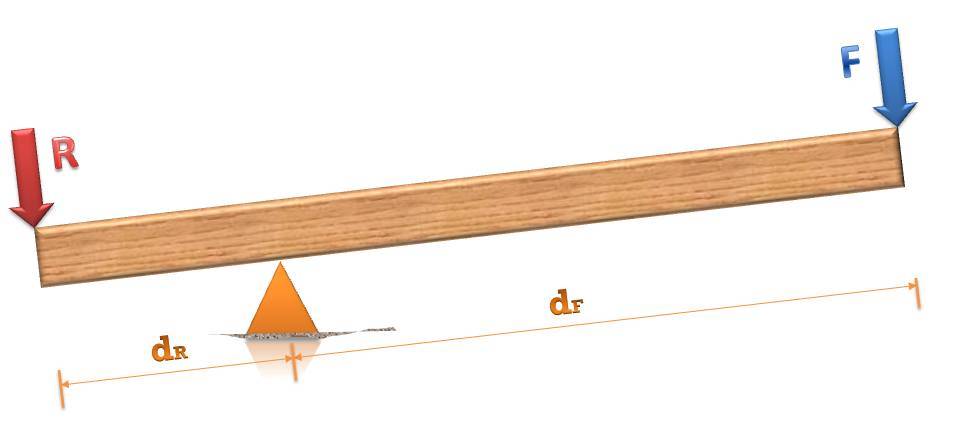
Рассмотрим классический рычаг с двумя плечами, когда опора находится вдали от концов балки. Пример такого механизма изображен ниже.

Мы видим, что когда этот рычаг применяют для совершения физической работы, то на него действует две силы:

внешняя сила F, которую прикладывают для выполнения полезной работы;
сила R, которая оказывает сопротивление силе F (она выполняет отрицательную работу).

В большинстве случаев сила F создается усилием человека, а сила R представляет собой вес некоторого груза.

Рассматриваемый рычаг будет находиться в равновесии, и перестанет испытывать вращение только тогда, когда сумма действующих на него моментов будет равна нулю. Используя обозначения рисунка выше, и применяя формулу для M, запишем правило равновесия рычага:

Заметим, что момент силы F записан со знаком минус, поскольку он стремится повернуть плечо рычага по часовой стрелке. Остается перенести второй член в правую часть равенства, чтобы записать правило рычага:

Таким образом, равенство моментов силы действия F и силы противодействия R является достаточным условием равновесия рассматриваемого простого механизма.

Кто установил правило равновесия рычага? Этот вопрос отчасти пересекается с рассмотренным выше историческим. Поскольку сохранились только письменные свидетельства научной деятельности Архимеда, связанной с этим механизмом, то именно он в настоящее время считается тем философом, кто установил правило рычага.

Равновесие рассматриваемой системы обеспечивается не только равенством нулю суммы моментов, но также равенством нулю всех действующих сил. Выше были названы лишь две силы (F и R). На самом же деле существует еще сила реакции опоры, направленная против сил F и R. Реакцию опоры момента силы не создает ввиду нулевой длины ее плеча.

Видео:Момент силы относительно точки и осиСкачать

Выигрыш и проигрыш в использовании рычага

Следует четко понимать, что при использовании рычага сохраняется полная энергия системы. Чтобы поднять груз на некоторую высоту, необходимо совершить определенную работу. Поскольку в формуле правила рычага стоит произведение силы на длину плеча, то отмеченную работу можно выполнить как с помощью большей силы, так и с помощью меньшей. Однако в первом случае необходимо будет переместить плечо рычага в вертикальном направлении на малую величину, во втором же случае — на большую величину. Это и есть выигрыш и проигрыш в использовании рычага.

Заметим, что в формуле правила рычага стоят значения моментов. Никакого отношения к работе они не имеют. Момент силы выполняет работу только тогда, когда система за счет его действия поворачивается вокруг оси на некоторый угол.

Видео:РЫЧАГ МОМЕНТ СИЛЫ физика 7 класс ПерышкинСкачать

Виды рычагов

Выше уже упоминалось, что все рычаги относятся к одному из трех типов. В основе классификации лежит относительное расположение сил R, F и опоры. Охарактеризуем все три типа:

Рычаг 1-го типа, или рода, был показан выше. Опора расположена в нем между силами R и F. В зависимости от длины плеч d_R и d_F его можно использовать как для выигрыша в пути, так и для выигрыша в силе. Примером этого типа рычага являются ножницы, весы, гвоздодер.
Рычаг 2-го рода предполагает, что сила R приложена между опорой и силой F. В таком случае получается выигрыш только в силе. Примерами таких рычагов в быту являются орехокол или ручная тачка.
Рычаг 3-го рода предполагает, что сила F расположена между опорой и грузом R. В этом случае выигрыш возможен только в пути. Использование лопаты, циркуля или удочки для рыбалки — это яркие примеры рычага 3-го рода в работе.

Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

Простой механизм блок

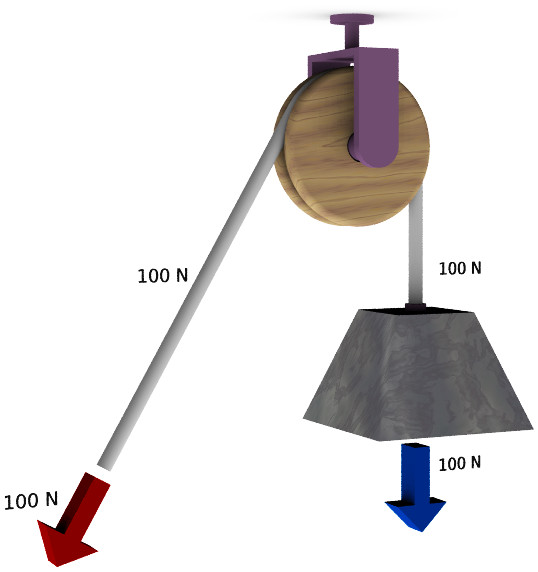
Рассматривая правила рычага, полезно сказать несколько слов о еще одном простом механизме — блоке. Представляет он собой обычный цилиндр с осью вращения, который имеет углубление по периметру своей боковой поверхности. Пример использования неподвижного блока показан ниже.

Как видно, выигрыша в силе и пути не происходит, однако неподвижный блок позволяет изменить направление воздействующей силы F.

Применение правила равновесия рычага к блоку производят, когда требуется рассчитать выигрыш в силе при использовании подвижных блоков. Один такой блок позволяет выиграть в 2 раза в силе и во столько же раз проиграть в пути.

Видео:Учимся решать задачи по биомеханике, простой способ определить направление момента силы. #FPAСкачать

Решение задачи

Ручная тачка сделана таким образом, что центр массы груза в ней находится на расстоянии 1/3*l от колеса, где l — длина тачки. Какой массы груз может переместить с помощью тачки человек, если известно, что он может приложить максимальную вертикальную силу F = 200 Н.

Воспользуемся правилом рычага, получим:

m = 3*F/g = 3*200/9,81 ≈ 61 кг.

Отметим, что сила F = 200 Н равна весу тела массой всего 20,4 кг. Таким образом, данная ручная тачка позволяет выиграть в 3 раза в силе.

Видео:Рычаг, момент силы. Физика 7 классСкачать

Вектор силы в рычаг

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

Видео:Vector W8 - это безумнейший когда-либо выпускавшийся суперкарСкачать

Рычаг. Равновесие сил на рычаге

Содержание

С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.

Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.

Рисунок 1. Строительство пирамид по Геродоту (гравюра XVIII века).

В данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.

Видео:Момент силы. Рычаги в природе, технике, быту | Физика 7 класс #44 | ИнфоурокСкачать

Устройство рычага

Рычаг — это любое твердое тело, которое может вращаться вокруг неподвижной опоры.

Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.

На камень действует сила — вес $P$. Для того чтобы поднять камень, необходимо преодолеть его вес, направленный вертикально вниз. В первом случае (рисунок 2, а) Образавр давит на конец палки с силой $F$, а во втором (рисунок 2, б) — поднимает конец палки.

В обоих случаях у этого рычага есть неподвижная точка опоры — точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.

Сила, с которой Образавр действует на палку (рычаг) меньше веса камня, но, тем не менее, у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.

Таким образом, рычаги бывают двух видов (рисунок 3):

Рисунок 3. Виды рычагов.

Рычаг 1-ого рода — сила приложены по обе стороны от точки опоры (рисунок 3, 1).
Рычаг 2-ого рода — силы приложены по одну сторону от точки опоры (рисунок 3, 2).

Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.

Видео:Весы РоберваляСкачать

Условие равновесия рычага

На рисунке 4 изображен рычаг. Его Точки A и B — это точки приложения сил $F_1$ и $F_2$ соответственно. Точка опоры O расположена между точками A и B — значит, перед нами рычаг 1-ого рода.

Рисунок 4. Рычаг.

А теперь взгляните на схему этого рычага (рисунок 4). Силы $F_1$ и $F_2$ направлены в одну сторону.

Рисунок 5. Схематическое изображение рычага.

Длина отрезка OA обозначена как $l_1$, а длина отрезка OB — $l_2$. Эти величины называются плечом силы.

Плечо силы — это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.

Тогда, OA или $l_1$ = это плечо силы $F_1$, а OB или $l_2$ — плечо силы $F_2$.

Чтобы получить условие равновесия рычага, нужно провести опыты. К рычагу по обе стороны от точки опоры подвешиваются разные груза так, чтобы каждый раз рычаг оставался в равновесии. В каждом случае измеряются модули сил и их плечи. В нашем случае (рисунок 4) видно, что сила $2 space Н$ уравновешивает силу $4 space Н$. А плечо меньшей силы в 2 раза больше плеча большей силы.

С помощью таких опытов было установлено правило равновесия рычага:

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил

где $F_1$ и $F_2$ — силы, которые действуют на рычаг, $l_1$ и $l_2$ — плечи этих сил.

Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют — правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: “Дайте мне точку опору, и я переверну Землю!”.

Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.

Например, возьмем рычаг, у которого одно плечо будет в 2 раза больше другого (как на рисунке 4). Приложим к точке A силу в $100 space Н$. Тогда в точке B мы сможем уравновесить силу в $200 space Н$ (в 2 раза большую). Если нам нужно поднять более тяжелый груз, то можно увеличить плечо рычага $l_1$, к которому мы прикладываем силу.

Видео:Простые механизмы. Рычаг. Равновесие сил на рычаге | Физика 7 класс #43 | ИнфоурокСкачать

Примеры задач

Рабочий поднимает груз массой $300 space кг$ c помощью рычага (рисунок 1, а). Большее плечо силы рано $3 space м$, а меньшее — $0.6 space м$. Какую силу рабочий прикладывает к большему плечу рычага?

Дано:
$m = 300 space кг$
$l_1 = 3 space м$
$l_2 = 0.6 space м$
$g = 9.8 frac$
$F_1 — ?$

Показать решение и ответ

Решение:

Запишем правило равновесия рычага:

Выразим отсюда силу $F_1$, которую прикладывает к рычагу рабочий:

Сила $F_2$ — это вес груза $P$, который мы можем рассчитать формуле: $P = gm$. Подставим в нашу формулу и рассчитаем силу $F_1$:

$F_1 = F_2 cdot frac = gm cdot frac = 9.8 frac cdot 300 space кг cdot frac = 2940 space Н cdot 0.2 = 588 space Н$.

Ответ: $F_1 = 588 space Н$.

На рисунке 6 схематически изображен рычаг. Точка опоры находится в точке O. Одно деление на шкале рычага равно $10 space см$. Какую массу должен иметь груз, подвешенный в точке A, чтобы рычаг находился в равновесии?

Рисунок 6. Схематическое изображения рычага для решения задачи.

Дано:
$m_1 = 100 space г$
$m_2 = 200 space г$
$l_1 = 50 space см$
$l_2 = 20 space см$
$g = 9.8 frac$
$m_3 — ?$

СИ:
$0.1 space кг$
$0.2 space кг$
$0.5 space м$
$0.2 space м$

Показать решение и ответ

Решение:
Найдем силу, которая будет действовать на рычаг в точке B. Эта сила будет равна весу $P_2$, с которым груза массой $m_1$ и $m_2$ действуют на подвес. Обозначим эту силу $F_2$.

$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 frac cdot (0.1 space кг + 0.2 space кг) = 9.8 frac cdot 0.3 space кг approx 3 space Н$.

Запишем правило равновесия рычага:

Выразим отсюда и рассчитаем силу $F_1$, с которой будет действовать на рычаг груз неизвестной массы:

Сила $F_1$ будет равна весу $P_1$, с которым груз массой $m_3$ действуют на подвес:

Найдем массу груза:

$m_3 = frac = frac<9.8 frac> approx 0.1 space г = 100 space г$.