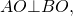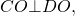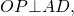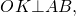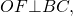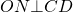Биссектрисы в трапеции окружность

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Биссектрисы трапеции | Осторожно, спойлер! | Борис Трушин !Скачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Биссектрисы углов параллелограмма или трапецииСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Биссектрисы трапеции и её свойстваСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Биссектрисы в трапеции #егэ2024 #алгебра #егэматематика #огэ #огэ2024 #алгебра #огэматематикаСкачать

Вписанная в трапецию окружность

Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?

1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.

1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.

2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.

O — точка пересечения

биссектрис трапеции ABCD.

3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,

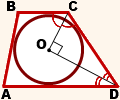
и точка O лежит на средней линии трапеции.

4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:

5.

6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:

Видео:БИССЕКТРИСА В ТРАПЕЦИИ. Мат в 3 хода!Скачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Задача про трапецию, описанную около окружностиСкачать

Биссектрисы трапеции

Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.

I. Биссектрисы углов при боковой стороне трапеции пересекаются.

1)∠ ABC+ ∠ BAD=180 º (как внутренние односторонние при AD ∥ BC и секущей AB).

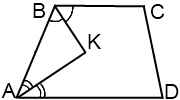
2) ∠ ABK+ ∠ KAB=( ∠ ABC+ ∠ BAD):2=90 º (так как биссектрисы делят углы пополам).

3) Так как сумма углов треугольника равна 180 º , в треугольнике ABK имеем: ∠ ABK+ ∠ KAB+ ∠ AKB=180 º , отсюда ∠ AKB=180-90=90 º .

Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.

Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.

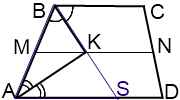
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN ∥ AD.

Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK ∥ AS.

Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.

II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.

В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.

Таким образом, BC=BK+KC=AB+CD.

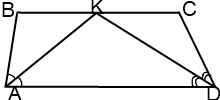
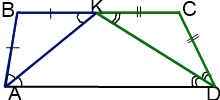
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.

В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.

III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.

В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.

Отсюда AD=AF+FD=AB+CD.

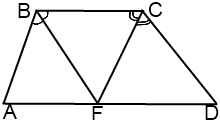
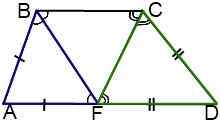
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.

У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.

📸 Видео

Геометрия Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хордыСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

✓ Пять способов решить задачу с параметром | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

Радиус описанной окружности трапецииСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Трапеция и вписанная окружностьСкачать

Сергей Шандарин: "Гигантская паутина Вселенной"Скачать

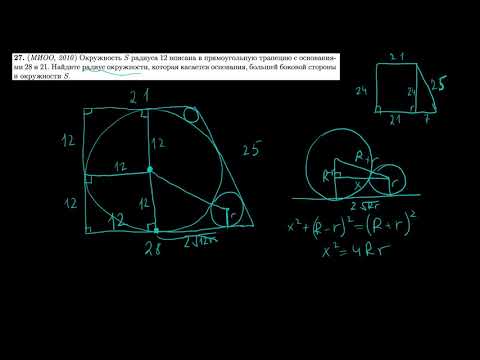
Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Бицентрический четырёхугольник. Вписанно-описанная трапецияСкачать

Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать