В различных школьных учебниках определение равных векторов даётся по-разному.
В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.
Два вектора называются равными, если они совмещаются параллельным переносом.
(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Равенство векторов обозначают так:
(Свойства равных векторов)
1) Равные векторы сонаправлены и имеют равные длины.
2) Равные векторы имеют равные координаты.
3) От любой точки можно отложить вектор, равный данному, и притом только один.
1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.
2) Пусть дан вектор
с началом в точке A(x1; y1) и концом в точке B(x2; y2).
По определению равных векторов, вектор
равный данному, получен из
Если этот параллельный перенос задан формулами
Найдём координаты каждого из векторов:
То есть координаты равных векторов
Что и требовалось доказать.
Таким образом, координаты задают длину и направление вектора, но не фиксируют его.
3) Пусть даны вектор
и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор
При таком параллельном переносе вектор
переходит в вектор
По определению равных векторов,
Что и требовалось доказать.
На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).
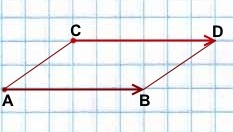
отложенный от точки C, равен вектору
(Признаки равенства векторов)
1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.
2) Если у векторов соответствующие координаты равны, то векторы равны.
1) 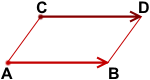
сонаправлены и имеют одинаковые длины.
Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор
переводит в вектор
По определению равных векторов,
Что и требовалось доказать.
2) Пусть векторы
Параллельный перенос, заданный формулами
переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы
А это означает, что
Что и требовалось доказать.
В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.
Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.
Видео:Геометрия 9 Откладывание вектора от данной точкиСкачать

Геометрия. 9 класс
Некоторые физические величины, например, сила или скорость характеризуются не только числовым значением, но и направлением. Такие величины называются векторными: F ⃗ – сила, v ⃗ – скорость.
Дадим геометрическое определение вектора.
Вектором называется отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом.
На чертежах вектор изображается отрезком со стрелкой, указывающей конец вектора. Вектор обозначают двумя заглавными латинскими буквами со стрелкой над ними. Первая буква обозначает начало вектора, вторая – конец.
Вектор можно обозначить и одной строчной латинской буквой со стрелкой над ней.
Длиной вектора называется длина отрезка, который изображает этот вектор. Для обозначения длины вектора используют вертикальные скобки.
Вектор, у которого конец совпадает с началом, называется нулевым вектором. Нулевой вектор изображается точкой и обозначается двумя одинаковыми буквами или нулём со стрелкой над ним. Длина нулевого вектора равна нулю: |0 ⃗|= 0.
Введём понятие коллинеарных векторов. Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считают коллинеарным любому вектору.
Если ненулевые коллинеарные векторы имеют одинаковое направление, то такие векторы будут сонаправленными. Если их направления противоположны – они называются противоположно направленными.
Для обозначения сонаправленных и противоположно направленных векторов существуют специальные обозначения:
— m ⃗ ↑↑ р ⃗, если векторы m ⃗ и р ⃗ сонаправлены;
— m ⃗ ↑↓ n ⃗ , если векторы m ⃗ и n ⃗ противоположно направлены.
Рассмотрим движение автомобиля. Скорость каждой его точки является векторной величиной и изображается направленным отрезком. Так как все точки автомобиля движутся с одинаковой скоростью, то все направленные отрезки, изображающие скорости разных точек, имеют одинаковое направление и их длины равны. Этот пример даёт нам подсказку, как определить равенство векторов.
Два вектора называются равными, если они сонаправлены и их длины равны. Равенство векторов можно записать с помощью знака равно: a ⃗ = b ⃗, KH ⃗ = OE ⃗
Если точка Р начало вектора р ⃗, то считают, что вектор р ⃗ отложен от точки Р.
Докажем, что от любой точки О можно отложить вектор, равный данному вектору р ⃗, и притом только один.
Доказательство:
1) Если р ⃗ – нулевой вектор, то ОО ⃗ = р ⃗.
2) Если вектор р ⃗ ненулевой, точка Р – начало этого вектора, а точка Т – конец.
Проведём через точку О прямую, параллельную РТ. На построенной прямой отложим отрезки ОА1 и ОА2, равные отрезку РТ.
Выберем из векторов ОА1 и ОА2 вектор, который сонаправлен с вектором р ⃗. На нашем чертеже это вектор ОА1. Этот вектор будет равен вектору р ⃗. Из построения следует, что такой вектор единственный.
Видео:Откладывание вектора от данной точки | Геометрия 7-9 класс #78 | ИнфоурокСкачать

§ 30. Векторы
30.1 Понятие вектора
Как вы знаете из физики и планиметрии, векторными величинами или, короче, векторами называются величины, которые характеризуются не только численным значением при выбранной единице измерения, но и направлением. Численное значение вектора называется его модулем или абсолютной величиной. Особый случай представляет нулевой вектор — его модуль равен нулю, а направления он не имеет.
Ненулевые векторы изображаются направленными отрезками. Напомним, что направленным отрезком называется отрезок, у которого указан порядок концов: первый называется началом, второй — концом. Направленные отрезки также называют векторами.
Вектор с началом А и концом В обозначается 

30.2 Сонаправленность и равенство векторов
Ненулевые векторы 





Из этого определения и сонаправленности двух лучей, сонаправленных с третьим (лемма п. 15.1), вытекает признак сонаправленности векторов: два вектора, сонаправленные с третьим вектором, сонаправлены.
Ненулевые векторы называются равными, если их длины равны и они сонаправлены. Равенство нулевых векторов определяется лишь первым из этих условий.
Итак, равенство 






Из данного определения и признака сонаправленности векторов следует признак равенства векторов: два вектора, равные третьему вектору, равны. Действительно, длины у них равны, а направление у них одно и то же, так как два вектора, сонаправленные с третьим, сонаправлены.
Отложить от данной точки вектор, равный данному, — значит построить направленный отрезок с началом в этой точке, изображающий данный вектор. От любой точки в пространстве можно отложить вектор, равный данному, и притом только один.
Действительно, пусть заданы вектор 


Напомним ещё, что два вектора называются коллинеарными (или параллельными), если изображающие их направленные отрезки параллельны или лежат на одной прямой. Аналогично определяется параллельность и перпендикулярность векторов прямым и плоскостям. О двух параллельных, но несонаправленных ненулевых векторах говорят, что они направлены противоположно. Параллельность, перпендикулярность и противоположная направленность векторов 







30.3 Сложение векторов
Как и в планиметрии, сумму двух векторов можно найти по правилу треугольника (рис. 262, а). А именно если даны два вектора 













Полученный результат не зависит от выбора точки А. А именно если взять другую точку А1 и отложить векторы 





Если векторы 








Свойства операций сложения векторов в стереометрии те же, что и в планиметрии, и доказываются они точно так же, как в планиметрии. Перечислим эти свойства, сопровождая их рисунками, из которых ясно, как они доказываются.
- Переместительное свойство, или коммутативность:
+
=
+
для любых векторов
и
(рис. 262, г).
- Сочетательное свойство, или ассоциативность:
+ (
+
) = (
+
) +
для любых векторов
,
,
(рис. 262, д).
- Свойство нуль-вектора:
+
= а для любого вектора
.
- Существование и единственность противоположного вектора: для каждого вектора
существует, и притом единственный, вектор —
, такой, что
+ (-
) =
(рис. 262, е).
Вычитание векторов — это операция, обратная сложению векторов. Вычесть из вектора 







По правилу параллелограмма сумма двух векторов, непараллельных одной прямой, представляется диагональю параллелограмма, построенного на данных векторах, отложенных от одной точки.
Аналогично сумма трёх векторов, непараллельных одной плоскости, представляется диагональю параллелепипеда, построенного на данных векторах, отложенных от одной точки, как на рёбрах (рис. 264). Убедитесь в этом.
30.4 Умножение вектора на число
Напомним определение умножения вектора на число, данное ещё в планиметрии.
Пусть даны ненулевой вектор 





Параллельный перенос сохраняет расстояния и направления, т. е. каждым двум точкам X, У сопоставляются такие точки Х’, У’, что 
А так как по (9) 
Итак, параллельный перенос — это движение. Оказывается, что любое движение в пространстве можно получить, последовательно выполняя два из трёх рассмотренных нами видов движений: отражение в плоскости, поворот вокруг прямой и перенос. А именно справедлива следующая
| Теорема (о классификации движений в пространстве): каждое движение в пространстве можно получить, последовательно выполняя либо поворот вокруг прямой и перенос вдоль этой прямой (такое движение называется винтовым, рис. 274, а), либо поворот вокруг прямой и отражение в плоскости, перпендикулярной этой прямой (такое движение называется зеркальным поворотом, рис. 274, б), либо отражение в плоскости и перенос вдоль этой плоскости (такое движение называется скользящим отражением, рис. 274, в). |
Доказательство этой теоремы мы не приводим.
💡 Видео
Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

81. Откладывание вектора от данной точкиСкачать

Построение отрезка равного данномуСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вычитание векторов. 9 класс.Скачать

8 класс, 42 урок, Откладывание вектора от данной точкиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Геометрия 10 класс (Урок№17 - Вектор в пространстве.)Скачать

Понятие вектора. Равенство векторов. Откладывание вектора от данной точкиСкачать

Сложение векторов. 9 класс.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

№743. Начертите ненулевой вектор a и отметьте на плоскости три точки A, B, C.Скачать
Координаты вектора в пространстве. 11 класс.Скачать

10.04 9a Откладывание вектора от данной точкиСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

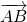
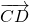
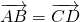
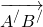
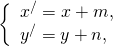

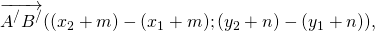
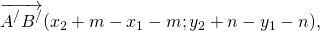
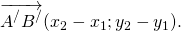
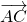

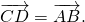
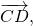
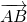
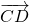
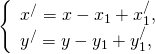
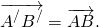



 = а для любого вектора
= а для любого вектора 



