Четырёхугольник ABCD вписан в окружность радиуса R = 10. Известно, что AB = BC = CD = 6.
а) Докажите,что прямые BC и AD параллельны.
а) Острые углы BCA и CAD равны, поскольку опираются на дуги стянутые равными хордами AB и CD. Значит, прямые BC и AD параллельны.
б) Обозначим угол BCA через α. По теореме синусов для треугольника ABC имеем
Треугольник ABC равнобедренный, поэтому Значит,
Четырехугольник ABCD — равнобедренная трапеция, поэтому
Значит,
По теореме синусов для треугольников ACD и ACB получаем: откуда, используя формулу синуса тройного угла, получаем:
Приведем другое решение пункта б)
Заметим, что центр описанной окружности лежит вне трапеции. Проведем две высоту трапеции BH — из вершины B и параллельную ей прямую EF проходящую через центр окружности. Обозначим AE = x, OE = y. Тогда из треугольника AOE по теореме Пифагора имеем а из треугольника BOF:
Тогда высота трапеции
а AH = x – 3. Напишем теорему Пифагора для треугольника ABH:
Подставим полученный результат в первое уравнение и решим его.
Очевидно, что нам подходит только положительный корень, откуда AD = 2x = 15,84.
Приведем решение пункта б), присланное читателем сайта.
Так как AB = BC = CD, эти хорды стягивают равные дуги. Значит,
По теореме синусов для треугольника ABC имеем:
откуда
Опустим высоту BH на основание AD. Тогда
Ответ: б)
| Критерии оценивания выполнения задания | Баллы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:Параллельные прямые | Математика | TutorOnlineСкачать  Решение задачи №16 с настоящего ЕГЭ 2018Условие задачи Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12. а) Докажите,что прямые BC и AD параллельны. Решение а) Докажем, что BC∥AD. Равные дуги стягиваются равными хордами. Дуги АВ и CD, стягиваемые равными хордами АВ и CD, равны. Значит, ∠АСВ=∠CAD — как опирающиеся на равные дуги. Эти углы — накрестлежащие при прямых BC и AD и секущей АС. б) Найдем AD, если АВ=ВС=CD=12, R=8. — так как опираются на равные хорды. Так как ABCD — равнобедренная трапеция, По теореме синусов из треугольника CDA: По теореме косинусов из △ACD: ‘ alt=’sin varphi =displaystyle frac = >’ /> x=12 или х =9. Видео:Геометрия Хорда AB и CD равны (см. рис.). Докажите, что дуга AMB = дуге CNDСкачать  Отрезки и прямые, связанные с окружностью. Теорема о бабочке
Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать  Отрезки и прямые, связанные с окружностью
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Круг |  Конечная часть плоскости, ограниченная окружностью Радиус |  Отрезок, соединяющий центр окружности с любой точкой окружности Хорда |  Отрезок, соединяющий две любые точки окружности Диаметр |  Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности Касательная |  Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания Секущая |  Прямая, пересекающая окружность в двух точках Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать  Свойства хорд и дуг окружности
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. Диаметр, проходящий через середину хорды |  Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. Равные хорды |  Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. Хорды, равноудалённые от центра окружности |  Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. Две хорды разной длины |  Большая из двух хорд расположена ближе к центру окружности. Равные дуги |  У равных дуг равны и хорды. Параллельные хорды |  Дуги, заключённые между параллельными хордами, равны. Видео:Геометрия Хорды AB и CD окружности не пересекаются, а прямые AB и CD пересекаются в точке M см. рисСкачать  Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Касательная и секущая, проведённые к окружности из одной точки | Секущие, проведённые из одной точки вне круга | Видео:ЕГЭ задание 16Скачать  Доказательства теорем о длинах хорд, касательных и секущихТеорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1). Тогда справедливо равенство Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство откуда и вытекает требуемое утверждение. Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2). Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство откуда и вытекает требуемое утверждение. Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3). Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство Доказательство . Проведём из точки A касательную AB к окружности (рис. 4). Точка B – точка касания. В силу теоремы 2 справедливы равенства откуда и вытекает требуемое утверждение. Видео:Окружность, диаметр, хорда геометрия 7 классСкачать  Теорема о бабочкеТеорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны. Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения: Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим Воспользовавшись теоремой 1, получим Воспользовавшись равенствами (1) и (2), получим Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство откуда вытекает равенство что и завершает доказательство теоремы о бабочке. 🎦 Видео№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  №189. Используя данные рисунка 108, докажите, что BC||AD.Скачать  №121. Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC. а) Докажите, что ΔСВОСкачать  Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  ЕГЭ математика 2023 вариант 3 задача 16 ПланиметрияСкачать 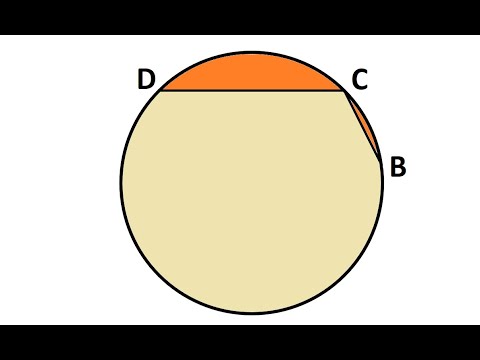 №651. Хорды АВ и CD окружности с центром О равны, а) Докажите, что две дуги с концами А и ВСкачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  №190. На рисунке 109 АВ=BC, AD=DE, ∠C=70°, ∠EAC = 35°. Докажите, что DE||АС.Скачать  Геометрия Докажите, что если две дуги окружности равны, то равны и хорды, их стягивающиеСкачать 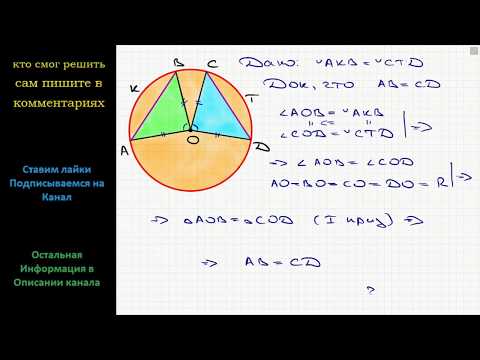 Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Отрезки и прямые, связанные с окружностью
Отрезки и прямые, связанные с окружностью



































