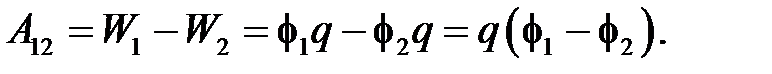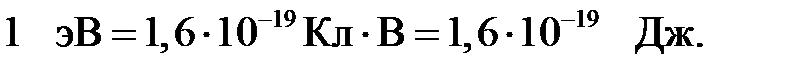Потенциал через радиус вектор (6 видео) | Курс школьной геометрии

Потенциал электростатического поля

Принцип суперпозиции для вектора напряженности электростатического поля

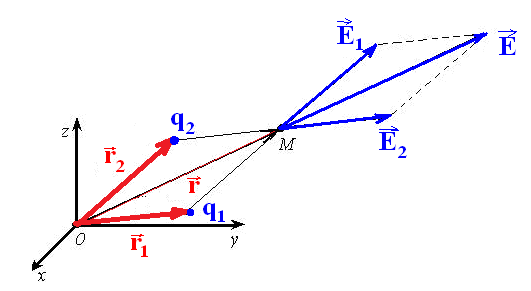Рис. 12.2.

Сложение выполняется по правилу треугольника или параллелограмма, «геометрически», по правилу сложения векторных величин, то есть покоординатно:

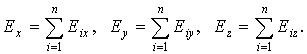(12.2)

Силовая линия. Векторное поле

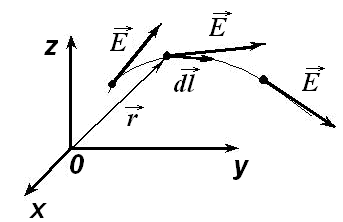Рис. 12.3.1Силовая линия вектора напряженности электростатического поля. Векторное поле

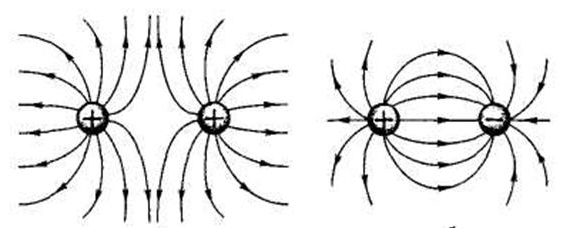
рис. 12.3.2 Примеры линий напряженности зарядовых систем

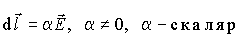(12.3)

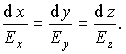(12.4)

Пользуясь понятием «силовая линия векторного поля», следует иметь в виду два обстоятельства:

Силовых линий существует бесконечное множество.

Силовая линия сама по себе не содержит информации о величине вектора, величину вектора в окрестности элементарной площадки задает густота линий.

Потенциал электростатического поля

Разные пробные заряды q’,q»,… будут обладать в одной и той же точке поля разными потенциальными энергиями. Однако отношение энергии к зарядубудет для всех зарядов одним и тем же. Поэтому можно вести скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал.

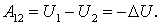
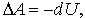
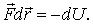При перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. Это относится и к элементарному перемещению или

(12.5)

: Поделив обе части на т и обозначив получим

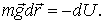
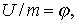
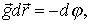(12.6)

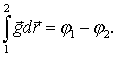(12.7)

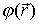
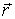
Функцию называют потенциалом поля в точке с радиус-вектором .

Физический смысл имеет не потенциал, а разность потенциалов, поэтому договорились считать, что потенциал точки, удаленной в бесконечность, равен нулю.

Когда говорят «потенциал такой-то точки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность.

Потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность

(или наоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля). При этом потенциал больше нуля, если q > 0.

Электрическое поле, создаваемое системой неподвижных электрических зарядов обладает свойством потенциальности: работа электрического поля по перемещению постоянного точечного заряда вдоль замкнутого контура равна нулю.

Рассмотрим электрическое поле одиночного точечного электрического заряда :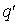

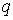
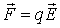Если в точке наблюдения помещен точечный заряд , то по определению:

(12.8)

где — сила, действующая на точечный заряд со стороны электрического поля .

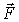
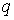
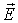
Элементарная работа по перемещению заряда из точки в точку в поле другого заряда:

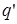
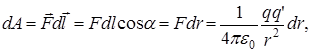
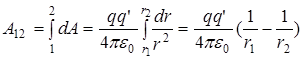
Найдем работу по перемещению пробного заряда из точки 1 в точку 2 в поле, создаваемом точечным зарядом q:

(12.9)

. (12.10)

И в этом случае работа сил не зависит от формы пути. Она является только функцией начального и конечного положения заряда.

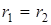
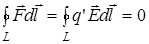
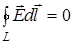
Для замкнутой траектории L она равна нулю, т. к. , т. е.

или (12.11 )

т.е. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ПО ЛЮБОМУ ЗАМКНУТОМУ КОНТУРУ РАВНА НУЛЮ.

В механике было приведено следующее определение: «Силы, работа которых не зависит от формы пути, называются консервативными силами, а поля, работа сил которых не зависит от формы пути, называются потенциальными полями». Таким образом, рассмотренное нами электростатическое поле является потенциальным, а кулоновские силы — консервативными.

1)Линии электростатического поля не могут быть замкнутыми.

Если поле создается системой зарядов, то, используя принцип суперпозиции, получаем:

Тогда и для потенциала или

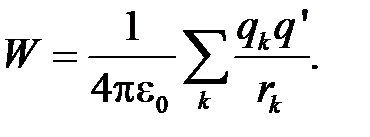
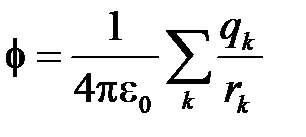
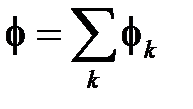
т.е. потенциал поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Выразим работу сил электростатического поля через разность потенциалов между начальной и конечной точками:

Или

За единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.

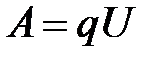
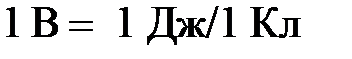
В СИ единица потенциала

Электрон — вольт (эВ) – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1 В, то есть:

Вектор «ротор» напряженности электрического поля :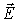

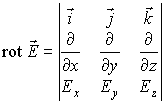где 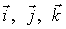— орты декартовой системы координат.

Условие потенциальности поля также имеет вид:

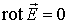(12.12)

Потенциал электростатического поля можно выразить иначе

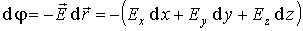(12.13)

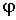
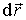
Дифференциал потенциала равен элементарной работе против сил электростатического поля, совершаемой над единичным точечным зарядом на перемещении .

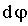
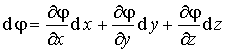Если учесть, что — полный дифференциал, т.е.:

(12.14)

то легко получить:

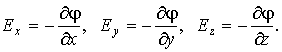(12.15)

В компактной форме записи:

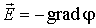(12.16)

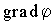
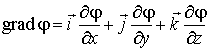где вектор определен соотношениями:

(12.17)

Градиент скалярного поля выделяет направление наискорейшего возрастания скалярной функции, а его модуль численно равен максимальной интенсивности возрастания этой функции.

Скалярное поле часто описывают с помощью «поверхностей уровня», эквипотенциальных или изоповерхностей, которые определяются уравнением

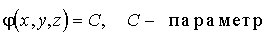(12.18)

На эквипотенциальной поверхности

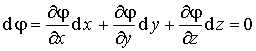(12.19)

что можно переписать в векторном виде:

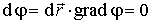,	(12.20)

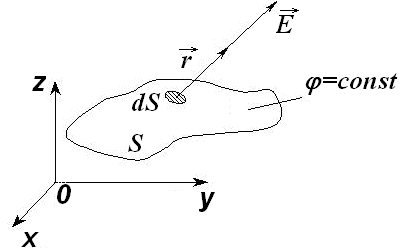Рис. 12.4. Эквипотенциальная поверхность и вектор напряженности электростатического поля

Вектор перпендикулярен любому вектору , принадлежащему поверхности , то есть перпендикулярен элементу площади поверхности .

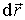
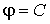
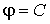
Следовательно, силовые линии электростатического поля перпендикулярны соответствующим элементам площади эквипотенциальной поверхности.

Иногда встречается обозначение

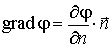(12.21)

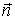
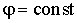
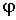
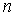
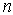
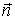
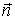
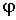
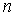
где — вектор единичной нормали (величина безразмерная!) к поверхности в точке, в которой вычисляется вектор , ориентированный в сторону увеличения ; — обозначение координаты ( — величина, имеющая размерность длины) вдоль направления . Таким образом — вектор, направленный вдоль описанного выше направления и численно равный производной от величины по координате вдоль этого направления.

Потенциал произвольной точки пространства определен с точностью до произвольной постоянной:

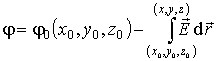(12.22)

При решении большого числа задач (но не всех!) удобно считать, что точка с координатами 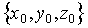расположена «на бесконечности», а потенциал ее равен нулю.

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Потенциал центрально-симметричного поля

Пусть электрическое поле имеет вид Ё(р) = Е(г)—, F — радиус-

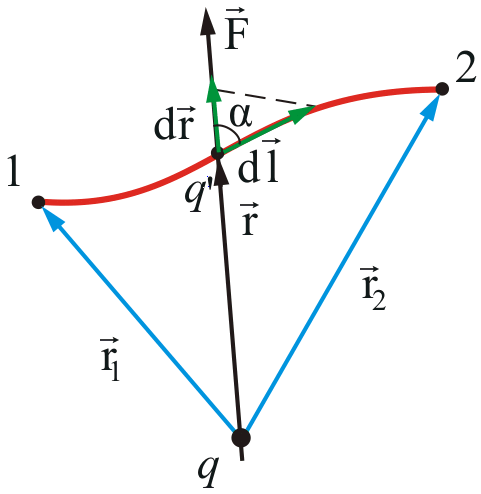
вектор (г = jc/ + у j + zk], г = (х 2 + у 1 + г 2 ) |/2 , Е(г) — некоторая функция. Ищем разность потенциалов между точками F_t = х,/ + yj + z_xk и г₂ = х₂/ +yj + z₂k (рис. 7.10).

Отметим особенность данного поля. Имеем |Ё(г) | = ^ |г| = Е(г) |

(если А = аа, а — число, то й = |а| • |а|), т. е. величина напряженности поля одинакова на сфере радиусом г, а направление вектора Е —

вдоль луча из начала координат (— = п — вектор единичной длины вдоль

такого луча). Поле обладает, как говорят, сферической симметрией.

Пусть / — некоторая кривая, ведущая из точки 1 в точку 2. Имеем:

Вектор d/ ведет из точки г в точку r+dr:F + dr=F + dl, т. е. dr = d/ и dr = dx / + dy j + dz k.

(учтено, что udu = ^d(u 2 )). Этот результат можно было получить еще проще: г dl = г dr = ^d(rr) = ^d(r ! ) = rdr. Таким образом,

Если функция Е(г) предъявлена, интеграл может быть взят.

Существенно, что координаты начальной и конечной точек входят в ответ лишь в комбинации (х 2 + у 2 + г 2 ) |/2 = г, т. е. разность потенциалов между любыми двумя точками, одна из которых взята на сфере г = г,, другая — на сфере г = r_v будет одна и та же.

На сфере х 2 + у 2 + г 2 = г 2 потенциал постоянен. Это следствие сферической симметрии.

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

1.3. Электрическое поле. Напряженность и потенциал поля

Вокруг всякого электрического заряда всегда существует электрическое поле.

Электрическое поле, созданное неподвижным зарядом (или системой неподвижных зарядов), называется электростатическим.

Посредством электростатического поля осуществляется взаимодействие между зарядами. Само понятие поля оказалось весьма плодотворным и широко используется в современной физике. Появление поля означает, что что-то изменилось в окружающем нас пространстве. Математически поле описывается величиной, меняющейся от точки к точке. Например, можно рассмотреть поле скоростей в текущей жидкости. В каждой точке объема жидкости задан вектор скорости, который может меняться со временем (нестационарное течение), а может и быть постоянным (стационарное течение). Это пример векторного поля. К этому же типу полей относится и поле неподвижных электрических зарядов.

Напишем выражение для силы, действующей на точечный заряд в результате его взаимодействия с системой точечных зарядов (соотношение Дополнения 1)

Здесь — радиус-вектор точки, в которой находится заряд . Заряд , на который, действует сила, в подобных ситуациях иногда называют «пробным» зарядом, выписан отдельным множителем. Выражение, стоящее в круглых скобках, определяется исключительно свойствами той системы зарядов, которая воздействует на заряд . Естественно, что это воздействие (сила) зависит от того, где он находится, соответственно, выражение в круглых скобках зависит от радиус-вектора , определяющего местоположение заряда . Следуя изложенной выше идее об электростатическом поле существующем вокруг каждого заряда и, разумеется, системы зарядов, введем силовую характеристику этого поля, называемую напряженностью электрического поля.

Напряженностью электрического поля называется вектор , равный отношению силы, действующей на точечный заряд к алгебраической величине этого заряда (рис. 1.12)

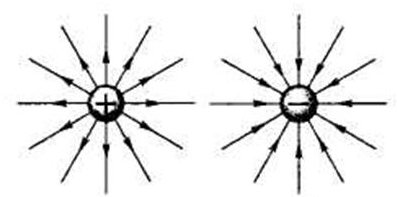
Рис. 1.12. Вектор напряженности электрического поля отрицательного и положительного точечного заряда

Из и определения напряженности вытекает, что напряженность поля произвольной системы покоящихся зарядов можно записать в виде

Действительно, сила, с которой данная система зарядов действует на точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы. Отсюда следует, что напряженность электрического поля системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы. Имеет место так называемый принцип суперпозиции (независимого наложения) электрических полей

Напряженность поля, созданного системой неподвижных заряженных тел, равна векторной сумме напряженностей полей, создаваемых каждым телом в отдельности:

Принцип суперпозиции является одним из наиболее общих принципов современной физики. Подчеркнем, что напряженности поля складываются векторно.

На рис. 1.13 иллюстрируется принцип суперпозиции полей на примере поля, создаваемого двумя точечными зарядами.

Рис. 1.13. Принцип суперпозиции электрических полей

Для одного заряда , находящегося в начале координат , для напряженности создаваемого им поля в точке с радиус-вектором получаем (индекс 1 опущен):

Напряженность поля точечного заряда в различных точках пространства, в общем случае различна и по величине и по направлению (рис. 1.14). Поле точечного заряда — центральное поле, центр симметрии поля совпадает с точкой, в которой находится заряд.

Рис. 1.14. Векторы напряженности электрического поля заряда q в разных точках пространства

В СИ единицей измерения напряженности электрического поля является ньютон на кулон (Н/Кл), — то есть за единицу напряженности поля принята напряженность такого поля, в котором на заряд равный 1 Кл действует сила, равная 1 Н:

На практике чаще употребляют другое название этой единицы — «вольт на метр» (В/м) (про единицу «вольт» речь пойдет несколько позже).

Характерные значения напряженностей электрических полей, встречающихся в нашем мире, приведены на рис. 1.15.

Рис. 1.15. Характерные значения напряженностей электрических полей, встречающихся в природе

Обратим внимание на сходство закона Кулона с законом всемирного тяготения

Роль зарядов играют массы, а гравитационная постоянная G аналогична коэффициенту Знак минус соответствует тому, что гравитационное взаимодействие всегда является притяжением. Можно ввести и вектор напряженности гравитационного поля как отношение силы , например, к пробной массе :

Если при этом — масса Земли, а её радиус, то есть ни что иное, как хорошо знакомое ускорение свободного падения м/с 2 (с точностью до весьма малой центробежной силы инерции, входящей в силу тяжести )

Пример 4. Среднее расстояние между электроном и протоном в атоме водорода равно r = 5,3·10 –11 м (рис. 1.16). Найти силы электростатического и гравитационного притяжения между ними и определить отношение этих сил.

Рис. 1.16. Электрон и протон в атоме водорода

Решение. Из закона Кулона имеем

В свою очередь из закона всемирного тяготения следует

Отношение сил не зависит от расстояния между электроном и протоном и равно

Этот расчет показывает, что в масштабах атомов и молекул силы гравитации столь меньше электростатических, что их можно не принимать во внимание.

Почему же в макромире, где мы обитаем, с законом гравитации мы знакомимся после первой же шишки на первых же шагах в детстве, а закон Кулона остается неизвестным многим из наших сограждан даже после окончания средней школы? Дело в том, что в макромире, как мы видели, положительные и отрицательные электрические заряды в телах скомпенсированы, так что в обычной жизни мы имеем дело с относительно небольшими избыточными зарядами. В то же время все тяготеющие массы имеют один и тот же знак, так что никакой компенсации масс не происходит, и силы гравитации проявляют себя в масштабах макромира в большей степени.

Электрическое поле можно задать, указав для каждой точки величину и направление вектора напряженности электрического поля . Для наглядного изображения электрического поля используют силовые линии (или линии векторного поля ).

Линией напряженности электрического поля (силовой линией) называется такая линия, касательная к которой в каждой её точке совпадает по направлению с вектором напряженности электрического поля.

На рис. 1.17 показана силовая линия электрического поля. Векторы напряженности электрического поля направлены по касательной к силовой линии.

Рис. 1.17. Векторы напряженности электрического поля направлены по касательной к силовым линиям

Число линий, пронизывающих перпендикулярную к ним площадку единичной площади, пропорционально величине (модулю) напряженности электрического поля в данном месте. Другими словами силовые линии проводятся гуще там, где модуль напряженности поля больше. Таким образом, конфигурация силовых линий позволяет судить об изменении направления и величины вектора в пространстве. Картина линий векторного поля (не обязательно электрического или магнитного) весьма наглядный графический способ отображения его основных свойств.

Отметим некоторые важные свойства силовых линий электростатического поля:

Рис. 1.18. Силовые линии точечного заряда: 1 — q > 0; 2 — q 3 . Было замечено, что капелька переставала падать при электрическом поле напряженностью 1,95·10 5 В/м. Это означало, что электростатическая сила qE компенсировала силу тяжести mg.

Масса капельки равна

Отсюда находим заряд капельки

то есть капелька несла пять электронных зарядов. Именно в таких экспериментах было обнаружено квантование электрического заряда и определена его минимальная величина e.

Движением заряженных частиц можно управлять, с помощью электрического поля нужной величины и направления. Так происходит, например, в электроннолучевой трубке осциллографа.

На рис. 1.24 показывается движение электронного луча, рисующего на экране электроннолучевой трубки с электрическим отклонением синусоиду. В осциллографе на вертикальные отклоняющие пластины подан усиленный исследуемый сигнал, а на горизонтальные — пилообразное напряжение развёртки. В результате электронный луч «рисует» зависимость исследуемого сигнала от времени на экране осциллографа.

Рис. 1.24. Принцип действия электроннолучевой трубки

Определение напряженности поля очень часто используется в виде

В силу определения (или, очевидным образом, это одно и то же) напряженность электрического поля называют его силовой характеристикой — оно определяет силу, действующую на заряд, помещенный в поле.

Пример 5. В пространство между пластинами плоского конденсатора влетает частица, движущаяся параллельно пластинам вдоль оси конденсатора (рис. 1.25). Начальную кинетическую энергию частица получила, пройдя ускоряющую разность потенциалов Под действием поля конденсатора частица отклоняется к одной из пластин (в зависимости от знака заряда) и в конечном итоге попадает на нее. Это расстояние можно измерить. Известно также расстояние между пластинами и напряжение на конденсаторе. Можно ли по этим данным установить тип частицы (найдя ее удельный заряд, т. е. отношение заряда к массе )?

Решение. Решим задачу сначала методом размерностей. Пройденное расстояние должно быть функцией параметров задачи:

Вспоминая, что произведение потенциала на заряд дает энергию, размерность которой получаем

Рис. 1.25. движение заряженной частицы между пластинами плоского конденсатора

Подставляя эту размерность, получаем уравнение:

Сравнивая размерности в обеих частях равенства, приходим к уравнениям:

Последнее уравнение, следующее из отсутствия в левой части величины размерности времени, сразу дает нам или После этого немедленно находим: Подставляя найденные значения, получаем:

Произвольная степень (показатель степени b определить не удалось) означает, что результат зависит от произвольной функции безразмерного отношения

Вид этой функции мы пока не знаем: если в задачу входят величины одинаковой размерности, то функцию их отношения с помощью анализа размерности найти, естественно, не удастся. Но мы уже можем ответить на вопрос задачи: в ответ не вошли параметры, характеризующие частицу — ни ее масса, ни ее заряд. Все частицы при заданных условиях будут отклоняться одинаково, и использовать такой прибор для их идентификации нельзя.

Приведем теперь точное решение задачи. Начальную скорость частицы находим из соотношения

В конденсаторе частица находится под действием электрического поля и приобретает поперечное ускорение Расстояние до попадания на пластину она пройдет за время t:

откуда находим время полета:

В продольном же направлении за это время частица пролетит расстояние

Мы приходим к тому же выводу о независимости от характеристик частицы. К тому же, теперь найдена функция оставшаяся не определенной в нашем предварительном результате.

В Главе 4 раздела «Механика» было показано, что консервативная сила связана с потенциальной энергией соотношением

Здесь знак — общепринятое обозначение векторного оператора «набла», результат действия которого на скалярную функцию координат есть градиент этой функции. Явный вид оператора набла в декартовых координатах следующий:

Подставив в и разделив на , получаем

Скалярная функция называется потенциалом электрического поля.

Функция , связанная с напряженностью электростатического поля соотношением

называется потенциалом электростатического поля.

Как видно из (1.13), потенциальная энергия точечного заряда в поле с потенциалом равна

а действующая на него сила

В Дополнении 3 разобран пример использования этих соотношений.

В СИ единицей измерения потенциала электрического поля является вольт (В):

Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал — его потенциальную энергию в этом поле. Поэтому, следуя смыслу соотношений и, напряженность электрического поля называют силовой характеристикой поля, а потенциал — его энергетической характеристикой.

Как и потенциальная энергия, потенциал поля всегда определен с точностью до аддитивной постоянной. Это видно из : поскольку набла есть дифференциальный оператор, потенциалы и физически тождественны, так как им соответствует поле одной и той же напряженности

Это позволяет нормировать потенциал, произвольно выбирая некоторую точку и полагая потенциал в этой точке равным нулю

Учитывая, что и напряженность поля, и потенциал поля убывают с ростом расстояния до системы зарядов, создающей поле, во всех тех случаях, когда конечный заряд распределен по конечной области пространства, нормировать потенциал естественно и удобно на «нуль на бесконечности», то есть полагать его равным нулю на бесконечном удалении от системы зарядов

О тех идеализированных случаях, когда нормировка на нуль на бесконечности, именно в силу идеализированности задачи, лишена смысла, будет сказано далее.

Соотношение (1.13) позволяет вычислить напряженность поля по известному потенциалу;

Получим «обратную» связь: выразим потенциал поля через его напряженность. Для этого сравним три выражения: выражение для из (1.18), выражение для вектора бесконечно малого перемещения и выражение для полного дифференциала функции :

Нетрудно видеть, что скалярное произведение двух первых векторов равно полному дифференциалу потенциала

На самом деле это соотношение не новое. Если умножить (1.20) на заряд и учесть связи (1.14) и (1.15), мы получим знакомое по главе 4 раздела «Механика» соотношение, связывающее работу консервативной силы и убыль потенциальной энергии

Там же, в разделе «Механика» было показано, что стационарное потенциальное поле консервативно. Из соотношения (1.18) вытекает, что электростатическое поле консервативно во всех тех случаях, когда потенциал поля не зависит от времени.

Интегрируя соотношение (1.20) от точки , потенциал в которой принят равным нулю, до некоторой точки , потенциал в которой нас интересует, вдоль произвольной, удобной для вычислений кривой (поле консервативно и от формы кривой результат не зависти), получаем

Вычислим с помощью (1.21) потенциал поля точечного заряда , находящегося в начале координат, нормировав его на нуль на бесконечном удалении от этого заряда. Воспользуемся для этого законом Кулона в форме (1.9):

При вычислении использовано тождество , справедливое для любого вектора : и являющееся результатом простого дифференцирования определения модуля любого вектора: .

Таким образом, потенциал поля точечного заряда находящегося в начале координат имеет вид

и поле это, как уже отмечалось ранее, центральное: фактически потенциал поля зависит только от .

Учитывая, что стоящей в знаменателе модуль радиус-вектора есть ни что иное как расстояние от заряда, создающего поле до точки наблюдения поля, формулу легко обобщить на случай, когда заряд находится не в начале координат, а в точке с радиус-вектором . В этом случае расстояние от заряда до точки наблюдения поля равно и потенциал поля в точке (при прежней нормировке на нуль на бесконечности) равен

Связь между напряженностью поля и его потенциалом линейная, поэтому принцип суперпозиции для напряженности поля справедлив и для потенциала поля. Другими словами: потенциал поля системы зарядов равен алгебраической сумме потенциалов поля от каждого из зарядов системы. Используя принцип суперпозиции, потенциал поля системы зарядов можно написать сразу :

Здесь — полное число зарядов в системе.

В случае непрерывного распределения заряда по некоторому объему , получим

При непрерывном распределении заряда по некоторой поверхности или кривой , получим соответственно

где и — соответствующие поверхностная и линейная плотности.

В Дополнении 4 разобран пример использования только что полученных соотношений.

Мы не будем рассматривать здесь отдельно вопрос о работе электростатических сил при перемещении в электростатическом поле точечных зарядов и заряженных тел. Электростатическое поле консервативно (рис. 1.26), потенциальная энергия заряда в поле равна , поэтому работа электростатических сил всегда может быть вычислена с помощью соотношений вида

Рис. 1.26. Работа электростатических сил зависит только от положения начальной и конечной точек

Вычислим энергию взаимодействия зарядов, входящих с состав некоторой системы.

Для нумерации этих зарядов удобно использовать два индекса, например, и . Одни и те же заряды системы, один раз это , другой раз это . Подчеркнем, что заряд и заряд это один и тот же 5-ый заряд системы. Такие «сложности» необходимы для компактной записи выражения для их энергии взаимодействия и вот почему. Заряды взаимодействуют попарно, энергия взаимодействия и зарядов согласно равна

Здесь — потенциал заряда в той точке, где находится заряд.

В — взаимодействие заряда самого с собой или его потенциальную энергию в собственном поле мы не рассматриваем.

Поэтому при суммировании энергий попарного взаимодействия зарядов мы обязательно должны учесть, что , во-первых, и, во вторых, каждая пара зарядов должна присутствовать в сумме только один раз. Это можно сделать двумя способами. Первый состоит в том, что при записи двойной суммы, явно оговаривается, например, что :

При втором способе, при соблюдении неравенства , суммирование ведется по всем возможным значениям и , соответственно, слагаемое, отвечающее взаимодействию одной и той же пары зарядов присутствует в сумме дважды, поэтому сумму необходимо разделить на 2. Получается:

В случае непрерывного распределения заряда по некоторому объёму с плотностью , соотношение, к примеру, принимает вид:

В первой из формул в (1.31) — потенциал всех зарядов кроме в той точке , в которой находится , во втором соотношении этот потенциал выписан явно, в третьей выполнена следующая операция: два интеграла, для краткости объединены в один и заряды и выражены через плотность заряда .

Мы не выписываем здесь формулы для случаев распределения заряда по поверхности или вдоль некоторой кривой, они лишь требуют замены в на и .

Для наглядного представления распределения потенциала в пространстве используются эквипотенциальные поверхности.

Эквипотенциальная поверхность (поверхность равного потенциала) — это совокупность точек, имеющих равный потенциал.

Рассмотрим картину эквипотенциальных поверхностей некоторых полей.

Напомним, что как из физических соображений, так и непосредственно из соотношения вытекает взаимная ортогональность силовых линий и эквипотенциальных поверхностей. Действительно, согласно определению, уравнение эквипотенциальной поверхности имеет вид

Дифференцируя это соотношение, получаем

для всех перемещений , касательных к эквипотенциальной поверхности. Значит вектор перпендикулярен эквипотенциальной поверхности. Осталось вспомнить, что вектор направлен по касательной к силовой линии по определению. Утверждение об ортогональности силовых линий и эквипотенциальных поверхностей доказано.

Эквипотенциальные поверхности поля точечного заряда представляют собой концентрические сферы с центром в точке нахождения заряда (см. рис. 1.27). Эквипотенциальные поверхности обозначены сплошными синими линиями, силовые линии — красными пунктирными линиями.

Рис. 1.27. Эквипотенциальные поверхности (сферы) (сплошные линии синего цвета) и силовые линии (пунктирные линии красного цвета) поля точечного заряда

Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные силовым линиям и расположенные на одинаковом расстоянии друг от друга (см. рис. 1.28).

Рис. 1.28. Эквипотенциальные поверхности однородного электрического поля

Эквипотенциальные поверхности поля двух одноименных одинаковых точечных зарядов представлены на рис. 1.29.

Рис. 1.29. Эквипотенциальные поверхности двух одноименных одинаковых точечных зарядов

Эквипотенциальные поверхности поля двух разноименных одинаковых по модулю точечных зарядов представлены на рис. 1.30.

Рис. 1.30. Эквипотенциальные поверхности двух разноименных одинаковых по модулю точечных зарядов

Графический вид двумерного (в плоскости z = 0) потенциала электрического поля, создаваемого точечным зарядом, расположенным в начале координат, показан на рис. 1.31.

Рис. 1.31. Вид двумерного (в плоскости z = 0) кулоновского потенциала 1/r вблизи положительного (1) и отрицательного (2) точечного зарядов. В случае (1) положительный пробный заряд натыкается на бесконечно высокий потенциальный барьер, препятствующий проникновению к центру. В случае (2) на пробный заряд действует сила притяжения, и он стремится скатиться в образовавшуюся потенциальную яму

Экспериментальное исследование потенциала поля вокруг заряженного металлического шара с помощью «пламенного» зонда показано на рис. 1.32. Используемый зонд присоединен к электрометру. Для выравнивания потенциала зонда с потенциалом той точки, где он находится, измерительный зонд помещается в пламя небольшой газовой горелки, обеспечивающей ионизацию воздуха и возможность стекания и натекания зарядов на зонд. Демонстрируется уменьшение потенциала при перемещении зонда по радиусу от центра шара и постоянство потенциала при движении зонда по окружности вокруг центра заряженного шара.