- Намагниченность. Токи намагничивания
- Молекулярные токи, их связь с вектором намагниченности
- Определение молекулярного тока
- Молекулярные токи и индукция магнитного поля
- Намагниченность
- Связь намагниченности с молекулярными токами
- Готовые работы на аналогичную тему
- Ответы на вопросы к коллоквиуму №2 (магнетизм). 1. Взаимодействие токов
- 15. Намагниченность J
- 16.*Токи намагничивания
- 17.*Связь тока намагничивания и намагниченности J
- 18. Напряженность магнитного поля H
- 19. Связь между векторами J и H
- 20. Магнитная восприимчивость
- 21. Связь векторов B и H
- 22. Магнитная проницаемость среды
- 23.*Граничные условия для вектора H
- 24.* Граничные условия для вектора B
- 25. Парамагнетики
- 26. Диамагнетики
- 27. Ферромагнетики
- 28. Домены
- 29. Температура Кюри
- 30. Магнитный гистерезис
- 31. Остаточная индукция
- 32. Коэрцитивная сила
- 33. Явление электромагнитной индукции
- 34. Токи Фуко
- 35.*Правило Ленца
- 36. Явление самоиндукции
- 37. Индуктивность
- 38. Энергия магнитного поля проводника с током
- 39.*Плотность энергии магнитного поля
- 40.*Ток смещения
- 🎦 Видео
Видео:ток намагничиванияСкачать

Намагниченность. Токи намагничивания
При внесении того или иного вещества в магнитное поле В0, например образованное токами в проводах, поле изменяется. Причиной является то, что ряд веществ являются магнетиками, т.е. способны под действием магнитного поля намагничиваться — приобретать магнитный момент. Намагниченное вещество создает свое магнитное поле В’. Результирующее поле
где В’ и В0 — поля, усредненные по физически бесконечно малому объему.
Как и поле 50, поле В’ не имеет точечных источников (магнитных зарядов). Следовательно, теорема Гаусса для результирующего поля в присутствии магнетика записывается так:
т.е. линии вектора В и при наличии вещества в магнитном поле непрерывны.
Механизм намагничивания. Известно, что молекулы многих веществ обладают собственным магнитным моментом из-за движения электронов по замкнутым микроскопическим орбитам в пределах каждой молекулы (атома). Каждому магнитному моменту соответствует молекулярный ток — элементарный круговой ток, создающий в окружающем пространстве магнитное поле. При отсутствии внешнего магнитного поля магнитные моменты молекул ориентированы беспорядочно. Тогда равны нулю и поле В’, и суммарный магнитный момент вещества. Во внешнем поле В0 магнитные моменты молекул приобретают преимущественную ориентацию и вещество намагничивается, возникает поле В’. Суммарный магнитный момент вещества будет отличен от нуля.
При внесении во внешнее поле веществ, молекулы которых не имеют при отсутствии поля В0 магнитного момента, в молекулах индуцируются молекулярные токи. Следовательно, вешество_приобретает магнитный момент, что и приводит к возникновению поля В’.
Таким образом, намагничивание вещества обусловлено преимущественной ориентацией или индуцированием микроскопических молекулярных токов во внешнем магнитном поле. Такое поведение молекулярных токов приводит к появлению макроскопических токов, называемых токами намагничивания Г. Токи намагничивания создают дополнительное магнитное поле В’. Токами проводимости называют текущие по проводникам токи, связанные с перемещением в веществе носителей тока. Отметим, что в отличие от токов проводимости токи намагничивания не приводят к перемещению заряда по магнетику.
Степень намагничивания магнетика характеризуется намагниченностью J — магнитным моментом единицы объема:
где AV — физически бесконечно малый объем в окрестности данной точки; рт — магнитный момент отдельной молекулы. Суммирование проводится по всем молекулам в объеме AV. Намагниченность можно также определить как
где п — концентрация молекул; (рт) — средний магнитный момент молекулы.
Если вещество намагничено однородно, то вектор J во всех точках магнетика одинаков.
Видео:Зазор в магнитопроводе и токи намагничиванияСкачать

Молекулярные токи, их связь с вектором намагниченности
Вы будете перенаправлены на Автор24
Видео:Модель намагничивания парамагнетикаСкачать

Определение молекулярного тока
Магнитное поле, подобно полю электрическому может быть макроскопическим и микроскопическим. Микроскопическое поле возникает в результате движения элементарных зарядов в веществе. Макроскопическое поле — результат усреднения микроскопических полей по бесконечно малым объемам пространства. Вращения электронов и ядер атомов по отношению к создаваемому ими магнитному полю эквивалентны токам, которые текут в атомах вещества. Средняя плотность такого тока в веществе равна нулю, переноса электрического заряда на макроскопические расстояния не происходит.
Итак, токи эквивалентные тем, которые возникают при движении элементарных зарядов в молекулах и атомах вещества, называют молекулярными токами.
В ненамагниченных магнетиках молекулярные токи распределены хаотично, их магнитные поля в среднем взаимно компенсируют друг друга. Намагниченный магнетик можно характеризовать упорядоченным характером молекулярных токов, благодаря чему результирующее магнитное поле вещества не равно нулю.
В тех магнетиках, которые являются проводниками (например, металлы) различают токи проводимости (плотность тока проводимости $overrightarrow<j_>$), которые относят к упорядоченному движению заряда в макроскопическом понимании (например, движению свободных электронов в металле) и молекулярные токи ($overrightarrow$), тогда микроскопическую плотность тока ($overrightarrow<j_>$) в среде вычисляют как:
Часто предполагают, что отличие токов проводимости от молекулярных токов в том, что молекулярные токи замыкаются внутри микроскопически малых объектов пространства. Подобное разделение токов на два типа упрощает вывод макро уравнений поля из посылок электронной теории.
Видео:Теорема о циркуляции вектора Н.МагнетикСкачать

Молекулярные токи и индукция магнитного поля
Для того, чтобы вычислить индукцию макроскопического поля молекулярные токи заменяют макроскопическими токами, которые непрерывно изменяются в пространстве. Такие токи имеют название токов намагничивания. Дальше эти плотность этих токов будем обозначать $overrightarrow$. Плотность токов проводимости будем обозначать $overrightarrow$. Так получаем, что магнитное поле порождается токами проводимости и токами намагничивания. Если известны эти токи, то можно вычислять индукцию поля $overrightarrow,$ используя формулы для вакуума. В таком случае теорема о циркуляции вектора индукции магнитного поля будет иметь вид:
или в дифференциальной форме:
где I — ток проводимости, $I_m$ — ток намагничивания, полные токи, которые пронизывают контур L.
Итак, возникновение магнитных моментов связано с наличием круговых токов. Токи в элементарных объемах, которые приводят к возникновению магнитных моментов, назвали молекулярными токами. Однако не следует воспринимать этот термин буквально. Молекулярные токи, строго говоря, могут течь только внутри молекулы. При определении намагниченности и других параметров имеют в виду усредненные величины. Магнитные моменты представляют размазанными по объему вещества, а молекулярные токи текущими по всему объему.
Видео:Магнитный гистерезисСкачать

Намагниченность
Для характеристики состояния намагниченного состояния магнетика используют вектор намагниченности $(overrightarrow)$.
Намагниченностью ($overrightarrow$) называют физическую величину, которая равна:
где $triangle V$ — элементарный объем, $overrightarrow<p_>$ — магнитные моменты молекул, суммирование осуществляется по всем молекулам в объеме $triangle V$. Из формулы (4) имеем, что:
Видео:Билет №17 "Магнитное поле в веществе"Скачать

Связь намагниченности с молекулярными токами
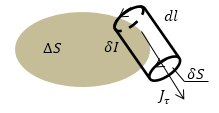
Рассмотрим бесконечно маленький замкнутый контур L, который ограничивает элемент площади $triangle S$ (рис.1). Вычислим циркуляцию намагниченности ($overrightarrow$) по контуру:
где $J_$- тангенциальная составляющая вектора намагниченности вдоль контура L. Эта составляющая возникает за счет токов, которые текут по замкнутым контурам вокруг линии, вдоль которой проводится интегрирование. Умножим и разделим правую часть выражения (6) на величину $delta S$ (площадь которую обтекает ток в плоскости, которая перпендикулярная линии интегрирования), проведем преобразования в том числе используя выражение (5):
В соответствии с определением магнитного момента ($p_m=ISto _m=delta Idelta S, $)$ где delta I сила тока, который обтекает площадку delta S,$ причем$ delta I$ пересекает $triangle S$ по нармали. Получаем из (7):
где $triangle I_n$- нормальная составляющая силы тока, которая пересекает площадку $triangle S.$ В результате мы получили:
Из выражения (9) легко получить:
Формула (10) — выражение для объемной плотности молекулярных токов, которые являются причиной намагниченности $overrightarrow$.
Молекулярные токи могут течь и по поверхности раздела меду магнетиками или между магнетиком и вакуумом. Тогда поверхностная плотность молекулярного тока ($i_=frac<triangle I_>$) равна:
где $overrightarrow$ — единичные вектор нормали к поверхности раздела, направленные во вторую среду.
Готовые работы на аналогичную тему
Задание: Получите формулу, связывающую объемную плотность молекулярных токов и вектор намагниченности ($overrightarrow=rotoverrightarrow$).
Найдем составляющую ротора вектора намагниченности в направлении нормали к площадке $triangle S (рис.1)$. Используем определение ротора и равенство (1.1):
$j_$— нормальная составляющая плотности молекулярных токов. Это логично, так как именно они отвечают за возникновение намагниченности.
Равенство (1.2) выполняется при любой ориентации площадки $triangle S,$ то есть для любых компонент $rotoverrightarrow $и $overrightarrow$. Следовательно, имеет место равенство:
Задание: Покажите, что поля постоянного магнита в виде цилиндра и поле соленоида с током эквивалентны.
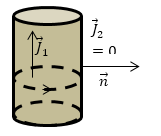
Найдем поверхностную плотность молекулярного тока однородного намагниченного цилиндра (рис.2), который является постоянным магнитом.
Намагниченность цилиндра ($overrightarrow$) изображена на рис.2 стрелкой. В вакууме намагниченность равна нулю $J_2=0.$ Нормаль $overrightarrow$ — внешняя нормаль к цилиндру. В соответствии с формулой:
плотность поверхностного молекулярного тока, который течет по цилиндру, равна:
[overrightarrow<i_>=overrightarrowtimes left(-overrightarrowright)=overrightarrowtimes overrightarrowleft(2.2right).]
Одна из линий тока показана как окружность со стрелкой. Намагниченность $overrightarrow$ составляет с текущим по поверхности током правовинтовую систему. Из формулы:
следует, что объемные молекулярные токи внутри цилиндра отсутствуют.
Ответ: Поле вне цилиндра создано поверхностными молекулярными токами, которые текут по окружностям. Этим доказано, что поля постоянного цилиндрического магнита и поле соленоида эквивалентны.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 10 02 2022
Видео:Урок 289. Магнитное поле в веществе. Магнитная проницаемость. Диа-, пара- и ферромагнетикиСкачать

Ответы на вопросы к коллоквиуму №2 (магнетизм). 1. Взаимодействие токов
| Название | 1. Взаимодействие токов |
| Анкор | Ответы на вопросы к коллоквиуму №2 (магнетизм).doc |
| Дата | 17.01.2018 |
| Размер | 1.04 Mb. |
| Формат файла |  |
| Имя файла | Ответы на вопросы к коллоквиуму №2 (магнетизм).doc |
| Тип | Документы #14423 |
| Категория | Физика |
| страница | 4 из 7 |
Подборка по базе: Практические задания 4^J5^J6 ответы.docx, Философия ответы.docx, Основы самообразования ответы.docx, Предпринимательство практические ответы.docx, История ответы практические.docx, МАКРОКОНОМИКА ответы.docx, Синергия ответы Информационные технологии в юридической деятельн, Итоговые тесты ПП ответы 2022.doc, Билеты и ответы.docx, гистология. ответы на вопросы к экзамену.docx15. Намагниченность JНамагниченность, характеристика магнитного состояния макроскопического физического тела; в случае однородно намагниченного тела Намагниченность определяется как магнитный момент Jединицы объёма тела: J = M/V, где М — магнитный момент тела, V — его объём. В случае неоднородно намагниченного тела Намагниченность определяется для каждой точки тела (точнее, для каждого физически малого объёма dV): J = dM/dV, где dM — магнитный момент объёма dV. Единица Намагниченность в Международной системе единиц — ампер на метр (1 а/м — Намагниченность, при которой 1 м 3 вещества обладает магнитным моментом 1 а×м 2 ), в СГС системе единиц — эрг/(гс×см 3 ); 1 эрг/(гс×см 3 ) = 10 3 а/м. Намагниченность тел зависит от внешнего магнитного поля и температуры (см. Парамагнетизм, Ферромагнетизм). У ферромагнетиков зависимость J от напряжённости внешнего поля Н выражается кривой намагничивания (см. Намагничивания кривые, Гистерезис). В изотропных веществах направление J совпадает с направлением Н, в анизотропных (см. Магнитная анизотропия) направления J и Н в общем случае различны. 16.*Токи намагничиванияТоки намагничивания I‘ . Намагничивание вещества связано с преимущественной ориентацией магнитных моментов отдельных молекул в одном направлении. Элементарные круговые токи, связанные с каждой молекулой, называютсямолекулярными. Молекулярные токи оказываются ориентированными, т.е. возникают токи намагничивания -. Токи, текущие по проводам, вследствие движения в веществе носителей тока называют токами проводимости — . Для электрона движущегося по круговой орбите по часовой стрелке; ток направлен против часовой стрелки и по правилу правого винта направлен вертикально вверх. Как же возникают токи намагничивания? Пусть есть цилиндр из однородного магнетика, — однородна, направлена вдоль оси. Молекулярные токи соседних молекул в местах соприкосновении с молекулярными точками других молекул текут в противоположные стороны и макроскопически компенсируют друг друга. Нескомпенсированными остаются только те токи, которые выходят на боковую поверхность цилиндра, эти токи и образуют макроскопический, поверхностный ток I¢, который циркулирует по боковой поверхности магнетика. Ток I¢создаёт такое же м.п., как все молекулярные токи вместе взятые.
тогда — подобен току, текущему в соленоиде с N=1 и создаёт внутри него поле, магнитную индукцию которого можно вычислить: , где — сила молекулярного тока, — длина рассматриваемого цилиндра, принята равной единице. Циркуляция вектора
Рассмотрим алгебраическую сумму токов , охватываемых контуром Г . Эта сумма равна , где -произвольная поверхность натянутая на контур Г. В алгебраическую сумму молекулярных токов входят только те молекулярные токи, которые оказываются «нанизанными» на контур. Токи не нанизанные на контур либо не пересекают натянутую на контур поверхность совсем, либо пересекают эту поверхность дважды – один раз в одном направлении, второй раз в другом. В результате их вклад в алгебраическую сумму токов, охватываемых контуром, оказывается равным нулю.
— теорема о циркуляции вектора (намагниченности). Циркуляция вектора намагниченности по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых контуром Г. Дифференциальная форма записи теоремы о циркуляции вектора .
Дифференциальная форма записи теоремы о циркуляции — формула (54.7) – ротор вектора намагниченности равен плотности тока намагничивания в той же точке пространства вещества. 17.*Связь тока намагничивания и намагниченности JПредставим атомы вещества цилиндра в виде одинаковых контуров, магнитные моменты которых ориентированы вдоль оси цилиндра. Стилизованный вид этих контуров в сечении, перпендикулярном оси цилиндра показан на Рис. 70. Такая упорядоченная структура молекулярных токов приводит к возникновению индуцированного тока, текущего по поверхности цилиндра (все токи внутри объема компенсируют друг друга). Такие токи, возникающие на поверхности намагниченного образца называются токами намагничивания. Обозначим высоту выделенной части цилиндра h. Тогда суммарная сила тока, текущего по поверхности этой части цилиндра может быть представлена в виде I‘ = i‘h , где i′ — линейная плотность поверхностного тока. Следовательно, магнитный момент рассматриваемой части цилиндра равен произведению силы поверхностного тока на площадь поперечного сечения цилиндра Pm = I‘S = i‘hS. С другой стороны по определению он равен произведению намагниченности вещества на объем выделенной части Pm = JV = JhS. Из сравнения этих двух выражений получаем важное соотношение: поверхностная плотность тока намагничивания равна модулю вектора намагниченности вещества Можно показать, что , когда вектор намагниченности не параллелен поверхности образца, плотность поверхностного тока равна тангенциальной составляющей вектора намагниченности В случае неоднородной намагниченности возможно возникновение токов намагниченности и внутри объема магнетика. 18. Напряженность магнитного поля HНапряжённость магни́тного по́ля — это векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности J. В СИ: , где μ0 — магнитная постоянная В системе СИ — в амперах на метр (А/м). В технике Эрстед постепенно вытесняется единицей СИ — ампером на метр, 1 Э = 1000/(4π) А/м = 79,5775 А/м. Напряжённость магнитного поля, векторная физическая величина (Н), являющаяся количественной характеристикой магнитного поля. Н. м. п. не зависит от магнитных свойств среды. В вакууме Н. м. п. совпадает с магнитной индукцией В; численно Н = В в СГС системе единиц и Н = В/m0 в Международной системе единиц (СИ), m0 — магнитная постоянная. В среде Н. м. п. Н определяет тот вклад в магнитную индукцию В, который дают внешние источники поля: Н = В — 4pj (в системе единиц СГС), или Н = (B/m0) — j (в СИ), где j — намагниченность среды. Если ввести относительную магнитную проницаемость среды m, то для изотропной среды Н = В/m0m (в СИ). Единицей Н. м. п. в СИ является ампер на метр (а/м), в системе единиц СГС — эрстед (э); 1 а/м = 4p×10 -3 э @ 1,256×10 -2 э. Н. м. п. прямолинейного проводника с током I (в СИ) Н = m0I/2pa (а — расстояние от проводника); в центре кругового тока Н = m0I/2R (R — радиус витка с током I); в центре соленоида на его оси Н = m0nI (n — число витков на единицу длины соленоида). Практическое определение Н в ферромагнитных средах (в магнитных материалах) основано на том, что тангенциальная составляющая Н не изменяется при переходе из одной среды в другую. При однородной намагниченности тела напряжённость, измеренная на его поверхности, параллельной направлению намагниченности, соответствует напряжённости внутри тела. Методы измерения Н. м. п. рассмотрены в ст.Магнитные измерения, Магнитометр. 19. Связь между векторами J и HМАГНИТНАЯ ВОСПРИИМЧИВОСТЬ (J или M) — величина, характеризующая связь намагниченностивещества с магнитным полем в этом веществе. М. в. М. в. достигает особенно больших значений в ФМ (от неск. десятков до многих тыс. единиц), причём ома очень сильно и сложным образом зависит от Н. Поэтому для ФМ вводят дифференциальную М. в. Кривая зависимости дифференциальной магн. восприимчивости х д ферромагнетиков от напряжённости намагниченного поля H (кривая А. Г. Столетова, 1872). В перем. магн. полях (синусоидальных) М. в.- комплексная величина (см. Магнитная проницаемость). М. в. анизотропных тел (ферроферримагнети-ков) — тензор. М. в. ФМ зависит от частоты перем. магн. поля. Эту зависимость изучает магн. спектроскопия. 20. Магнитная восприимчивостьМагнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе. Магнитная восприимчивость определяется отношением намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. По своему смыслу восприимчивость является величиной безразмерной. Иногда полезно ввести понятие удельной магнитной восприимчивостью, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратных килограммах (кг −1 ). Аналогично, молярнаямагнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях (моль −1 ). Реальные объекты могут обладать как положительными, так и отрицательными магнитными восприимчивостями. Примером веществ с отрицательной восприимчивостью могут служить диамагнетики — их намагниченность по направлению противоположна приложенному магнитному полю. Положительной восприимчивостью обладают, например, парамагнетики и ферромагнетики. Магнитная восприимчивость диамагнетиков и парамагнетиков мала и составляет величину порядка 10 −4 — 10 −6 , при этом она практически не зависит от напряжённости приложенного магнитного поля. Заметные отклонения наблюдаются только в области сильных полей или низких температур. В ферромагнетиках магнитная восприимчивость может достигать весьма больших значений, составляя величины от нескольких десятков до многих тысяч единиц, причём наблюдается её сильная зависимость от напряжённости приложенного поля. Поэтому для удобства используют также дифференциальную магнитную восприимчивость, равную производной намагниченности единицы объёма вещества по напряжённости поля. В отсутствии поля магнитная восприимчивость ферромагнетиков отлична от нуля и имеет некоторое положительное значение ka, называемое начальной магнитной восприимчивостью. С увеличением напряжённости поля величина восприимчивости растёт, пока не достигает некоего максимума kmax, после чего вновь уменьшается. В области очень сильных полей магнитная восприимчивость ферромагнетиков (при температурах, не очень близких к точке Кюри) падает практически до нуля, сравниваясь с величиной восприимчивости обычных парамагнетиках (эта область параметров называется областью парапроцесса). Вид зависимости магнитной восприимчивости ферромагнетика от напряжённости намагничивающего поля носит название кривой Столетова и обусловлен сложными механизмами намагничивания ферромагнетиков. 21. Связь векторов B и HСвязь между напряженностью магнитного поля, индукцией и намагниченностью где H – напряженность магнитного поля, B – индукция магнитного поля, m0 = 4p10 -7 В ∙ сек/А ∙ м = 4p10 -7 Гн/м – магнитная постоянная. где I – вектор интенсивности намагничения среды (намагниченность) – векторная сумма магнитных моментов, находящихся в единице объема. В изотропной среде: где m – относительная магнитная проницаемость среды. 22. Магнитная проницаемость средыМагнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и напряжённостью магнитного поля H в веществе. Впервые встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») в 1881 году [1] . В общем случае зависит как от свойств вещества, так и от величины и направления магнитного поля. Обычно обозначается греческой буквой μ. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных). В общем виде вводится следующим образом: Для изотропных веществ справедливо: В системе СГС магнитная проницаемость — безразмерная величина, в системе СИ вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости: где μr — относительная, а μ — абсолютная проницаемость, μ0 — магнитная постоянная (магнитная проницаемость вакуума). 23.*Граничные условия для вектора H24.* Граничные условия для вектора BГраничные условия для нормальных составляющих магнитного поля Обозначим векторные поля магнитной индукции соответственно изображению ниже в средах 1 и 2 В окрестности точки Р выделим цилиндрический объем с основаниями + поток через боковую поверхность. При стремлении От того, что справедлив во всех случаях закон неразрывности магнитных силовых линий сделаем запись Следовательно, на границе раздела двух сред нормальные составляющие вектора магнитной индукции непрерывны. Поскольку записано крайнее соотношение может быть относительно магнитного поля относительно напряженностей: Исходя из этого видно, что на границе раздела в общем случае напряженность магнитного поля испытывает скачок. 25. ПарамагнетикиПарамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы . Термин «Парамагнетизм» ввёл в 1845 году Майкл Фарадей, который разделил все вещества (кроме ферромагнитных) на диа— и парамагнитные. Атомы (молекулы или ионы) парамагнетика обладают собственными магнитными моментами, которые под действием внешних полей ориентируются по полю и тем самым создают результирующее поле, превышающее внешнее. Парамагнетики втягиваются в магнитное поле. В отсутствие внешнего магнитного поля парамагнетик не намагничен, так как из-за теплового движения собственные магнитные моменты атомов ориентированы совершенно беспорядочно. К парамагнетикам относятся алюминий (Al), платина (Pt), многие другие металлы (щелочные и щелочно-земельные металлы, а также сплавы этих металлов), кислород (О2), оксид азота (NO), оксидмарганца (MnO), хлорное железо (FeCl2) и др. Парамагнетиками становятся ферро- и антиферромагнитные вещества при температурах, превышающих, соответственно, температуру Кюри или Нееля (температуру фазового перехода в парамагнитное состояние). 26. ДиамагнетикиДиамагне́тики — вещества, намагничивающиеся против направления внешнего магнитного поля. В отсутствие внешнего магнитного поля диамагнетики немагнитны. Под действием внешнего магнитного поля каждый атом диамагнетика приобретает магнитный момент I (а каждый моль вещества — суммарный магнитный момент), пропорциональный магнитной индукции B и направленный навстречу полю. Поэтому магнитная восприимчивость χ = I/B у диамагнетиков всегда отрицательна. По абсолютной величине диамагнитная восприимчивость χ мала и слабо зависит как от напряжённости магнитного поля, так и от температуры. К диамагнетикам относятся инертные газы, азот, водород, кремний, фосфор, висмут, цинк, медь, золото, серебро, а также многие другие, как органические, так и неорганические, соединения. Человек в магнитном поле ведет себя как диамагнетик. Диамагнитная левитация имеет ту же природу что и эффект Мейснера (полное вытеснение магнитного поля из материала), она наблюдается при гораздо более сильных полях, но зато не требует предварительного охлаждения. Некоторые опыты доступны любителям. Например, редкоземельный магнит с индукцией около 1 Тл может висеть между двух пластин висмута. [2][3][4] А в поле с индукцией 11 Тл человеческие пальцы могут стабилизировать в воздухе, не касаясь, маленький магнит 27. Ферромагнетики28. Домены29. Температура КюриТочка Кюри, или температура Кюри, — температура фазового перехода II рода, связанного со скачкообразным изменением свойств симметрии вещества (например, магнитной — вферромагнетиках, электрической — в сегнетоэлектриках, кристаллохимической — в упорядоченных сплавах). Назван по имени П. Кюри. При температуре T ниже точки Кюри Q ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью и определённой магнитно-кристаллической симметрией. В точке Кюри (T = Q) интенсивность теплового движения атомов ферромагнетика оказывается достаточной для разрушения его самопроизвольной намагниченности («магнитного порядка») и изменения симметрии, в результате ферромагнетик становится парамагнетиком. Аналогично у антиферромагнетиков при T = Q (в так называемой антиферромагнитной точке Кюри или точке Нееля) происходит разрушение характерной для них магнитной структуры (магнитных подрешёток), и антиферромагнетики становятся парамагнетиками. В сегнетоэлектриках и антисегнетоэлектриках при T = Q тепловое движение атомов сводит к нулю самопроизвольную упорядоченную ориентацию электрических диполей элементарных ячеек кристаллической решётки. В упорядоченных сплавах в точке Кюри (её называют в случае сплавов также точкой Курнакова) степень дальнего порядка в расположении атомов (ионов) компонентов сплава становится равной нулю. Таким образом, во всех случаях фазовых переходов II рода (типа точки Кюри) при T = Q в веществе происходит исчезновение того или иного вида атомного «порядка» (упорядоченной ориентации магнитных или электрических моментов, дальнего порядка в распределении атомов по узлам кристаллической решётки в сплавах и т. п.). Вблизи точки Кюри в веществе происходят специфические изменения многих физических свойств (например, теплоёмкости, магнитной восприимчивости и др.), достигающие максимума при T = Q, что обычно и используется для точного определения температуры фазового перехода. Численные значения температуры Кюри приводятся в специальных справочниках. 30. Магнитный гистерезисГистере́зис (греч. ὑστέρησις — «отстающий») — свойство систем (обычно физических), которые не сразу следуют приложенным силам. Реакция этих систем зависит от сил, действовавших ранее, то есть поведение системы зависит от её собственной истории. Не следует путать это понятие с инерционностью поведения систем, которое обозначает стабильное сопротивление системы изменению её состояния. Магнитный гистерезис — явление зависимости вектора намагничивания и вектора напряженности магнитного поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках — Fe, Co, Ni и сплавах на их основе. Именно магнитным гистерезисом объясняется существование постоянных магнитов. Явление магнитного гистерезиса наблюдается не только при изменении поля H по величине и знаку, но также и при его вращении (гистерезис магнитного вращения), что соответствует отставанию (задержке) в изменении направления M с изменением направления H. Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H. Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания. Эти изменения обусловлены смещением доменных границ и ростом одних доменов за счёт других, а также вращением вектора намагниченности в доменах под действием внешнего магнитного поля. Всё, что задерживает эти процессы и способствует попаданию магнетиков в метастабильные состояния, может служить причиной магнитного гистерезиса. В однодоменных ферромагнитных частицах (в частицах малых размеров, в которых образование доменов энергетически невыгодно) могут идти только процессы вращения M. Этим процессам препятствует магнитная анизотропия различного происхождения (анизотропия самого кристалла, анизотропия формы частиц и анизотропия упругих напряжений). Благодаря анизотропии, M как бы удерживается некоторым внутренним полем HA (эффективным полем магнитной анизотропии) вдоль одной из осей лёгкого намагничивания, соответствующей минимуму энергии. Магнитный гистерезис возникает из-за того, что два направления M (по и против) этой оси в магнитоодноосном образце или несколько эквивалентных (по энергии) направлений М в магнитомногоосном образце соответствуют состояниям, отделённым друг от друга потенциальным барьером (пропорциональным HA). При перемагничивании однодоменных частиц вектор M рядом последовательных необратимых скачков поворачивается в направлении H. Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M коэрцитивная сила . Более универсальным является механизм неоднородного вращения M. Однако наибольшее влияние на Hc он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом Hc может быть существенно меньше эффективного поля анизотропии формы. В электронике и электротехнике используются устройства, обладающие магнитным гистерезисом — различные магнитные носители информации, или электрическим гистерезисом, например, триггер Шмитта или гистерезисный двигатель. 31. Остаточная индукция32. Коэрцитивная силаКоэрцитивная сила — такое размагничивающее внешнее магнитное поле напряженностью , которое необходимо приложить к ферромагнетику, предварительно намагниченному до насыщения, чтобы довести до нуля его намагниченность или индукцию магнитного поля внутри. Соответственно рассматривают коэрцитивную силу , полученную по циклу , или по циклу . Обозначают соответственно и Коэрцитивная сила всегда больше . Этот факт объясняется тем, что в правой полуплоскости графика гистерезиса значение больше, чем , на величину : В левой полуплоскости, наоборот, меньше, чем , на величину . Соответственно, в первом случае кривые будут располагаться выше кривых 33. Явление электромагнитной индукцииЭлектромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем в 1831 году. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина э.д.с. не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой э.д.с. , называется индукционным током. Согласно закону электромагнитной индукции Фарадея (в системе СИ): — электродвижущая сила, действующая вдоль произвольно выбранного контура, Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца: Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток. Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом: — магнитный поток через один виток, В дифференциальной форме закон Фарадея можно записать в следующем виде: или с помощью простейшей эквивалентной формулы: Здесь — напряжённость электрического поля, — магнитная индукция, C — произвольная площадка, — её граница. Следует отметить, что закон Фарадея в такой форме описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт вариации самого поля без изменения границ контура. Если магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС описывается силой Лоренца, хотя равенство Закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля. При выражении магнитного поля через векторный потенциал, закон Фарадея принимает форму: При учёте электростатического поля имеем: 34. Токи ФукоВихревые токи, токи Фуко (в честь Фуко, Жан Бернар Леон) — вихревые индукционные токи, возникающие в массивных проводниках при изменении пронизывающего их магнитного потока. Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами. Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфированияподвижных частей гальванометров, сейсмографов и др. Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления. С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации. Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными. 35.*Правило ЛенцаПравило Ленца, правило для определения направления индукционного тока: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток. Сформулировано в 1833 г. Э. Х. Ленцем. Если ток увеличивается, то и магнитный поток увеличивается. Если Если Индукционный ток всегда направлен так, чтобы уменьшить действие причины его вызывающей. 36. Явление самоиндукцииСамоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении тока, протекающего через контур. При изменении тока в контуре меняется магнитный поток через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи ЭДС препятствует возрастанию тока, а при уменьшении тока — убыванию. Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25 кВ. Что не совсем верно: бросок тока в первичной обмотке, вызванный самоиндукцией, создаёт ЭМ-импульс, который и создаёт высокое напряжение на вторичной обмотке. Также это явление применяется для поджига люминесцентных ламп в стандартной схеме. 37. ИндуктивностьИндукти́вность — коэффициент пропорциональности между магнитным потоком (создаваемым током какого-либо витка при отсутствии намагничивающих сред, например, в воздухе) и величиной этого тока [1][2] [3] . Если в проводящем контуре течёт ток, то ток создаёт магнитное поле [3] . Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом [3] : где L — индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду: где Если поток, пронизывающий каждый из витков одинаков, то Ψ = NΦ. Соответственно, LN = L1N 2 (суммарный магнитный поток увеличивается в N раз и потокосцепление еще в N раз). Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы. В системе единиц СИ индуктивность измеряется в генри [5] , сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10 9 см) [3] . Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени. Символ L, используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz) [ источник не указан 447 дней ] . Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry) [6] . Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года [ источник не указан 447 дней ] . Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [3] :
При заданной силе тока индуктивность определяет энергию магнитного поля тока [3] :
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности [3] . 38. Энергия магнитного поля проводника с токомМагни́тноепо́ле — составляющая электромагнитного поля, появляющаяся при наличии изменяющегося во времени электрического поля. Кроме того, магнитное поле может создаваться током заряженных частиц, либо магнитными моментами электронов в атомах (постоянные магниты). С точки зрения квантовой теории поля электромагнитное взаимодействие переносится безмассовым бозон-фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля). Основной характеристикой магнитного поля является его сила, определяемая вектором магнитной индукции (вектор индукции магнитного поля) [1] . В СИ магнитная индукция измеряется в теслах (Тл), в системе СГС в гауссах. Магнитное поле — это особый вид материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом. Можно также рассматривать магнитное поле, как релятивистскую составляющую электрического поля. Точнее, магнитные поля являются необходимым следствием существования электрических полей испециальной теории относительности. Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются свет и прочие электромагнитные волны. Энергия магнитного поля Приращение плотности энергии магнитного поля равно: — напряжённость магнитного поля, μii — диагональные компоненты этого тензора, μ0 — магнитная постоянная В изотропном линейном магнетике: μ — относительная магнитная проницаемость В вакууме μ = 1 и: Энергию магнитного поля в катушке индуктивности можно найти по формуле: Φ — магнитный поток, L — индуктивность катушки или витка с током. 39.*Плотность энергии магнитного поляПлотность энергии магнитного поля — физическая величина, равная отношению: — энергии магнитного поля в некотором объеме; к — величине этого объема. Объемная(пространственная) плотность энергии однородного магнитного поля (например, поля длинного соленоида) Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника: Т.к. в вакууме , имеем 40.*Ток смещенияТок смещения или абсорбционный ток — понятие из области теории классической электродинамики. Введено Дж. К. Максвеллом при построении теории электромагнитного поля для описания слабыхтоков, возникающих при смещении заряженных частиц в диэлектриках. В природе существует три вида токов: ток проводимости, ток смещения и ток переноса. Во времена Максвелла, ток проводимости мог быть экспериментально зарегистрирован и измерен (например,амперметром, индикаторной лампой), тогда как движение зарядов внутри диэлектриков могло быть лишь косвенно оценено. Ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля. При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания и объяснения «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения. Ток смещения существует и в проводниках, по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока: Для различия ток проводимости и ток смещения принято обозначать разными символами — i и j. В диэлектрике (например, в диэлектрике конденсатора) и в вакууме нет токов проводимости. Поэтому уравнение Максвелла пишется так — 🎦 Видео59. Магнитное поле в веществеСкачать  Урок 290. Объяснение свойств ферромагнетиковСкачать  Урок 172 (осн). Постоянные магниты. Гипотеза АмпераСкачать  Диамагнетики и парамагнетикиСкачать  Виды и способы намагничиванияСкачать  Поляков П. А. - Электромагнетизм - Магнетики. Молекулярные токи. НамагниченностьСкачать  Полюсный способ намагничивания магнитовСкачать  Запись лекции на тему "Комбинированное намагничивание. Намагничивающие токи. Размагничивание"Скачать  ПАРАДОКС ТРЁХ МАГНИТОВСкачать  1.2 Материальные уравнения, векторы поляризованности и намагниченности средСкачать  Техническое намагничивание ферромагнетиков (07 04 2018)Скачать  Лекция 3 Виды намагниченности (2021)Скачать  64. ФерромагнетизмСкачать  |






 в статич. полях равна отношению намагниченностивещества М к напряжённости Н намагничивающего поля:
в статич. полях равна отношению намагниченностивещества М к напряжённости Н намагничивающего поля:  ;
;  — величина безразмерная. М. в., рассчитанная на 1 кг (или 1 г) вещества, наз. удельной (
— величина безразмерная. М. в., рассчитанная на 1 кг (или 1 г) вещества, наз. удельной ( , где р — плотность вещества), а М. в. одного моля — молярной (или атомной):
, где р — плотность вещества), а М. в. одного моля — молярной (или атомной):  , где т — молекулярная масса вещества. С магнитной проницаемостью
, где т — молекулярная масса вещества. С магнитной проницаемостью  . в. в статич. полях (статич. М. в.) связана соотношениями:
. в. в статич. полях (статич. М. в.) связана соотношениями:  (в ед. СГС),
(в ед. СГС),  (в ед. СИ). М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля; положительной — парамагнетики (ПМ) и ферромагнетики (ФМ), они намагничиваются по полю. М. в. ДМ и ПМ мала по абс. величине
(в ед. СИ). М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля; положительной — парамагнетики (ПМ) и ферромагнетики (ФМ), они намагничиваются по полю. М. в. ДМ и ПМ мала по абс. величине  , она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р). Значения М. в. см. в табл.
, она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р). Значения М. в. см. в табл. , к-рая характеризует зависимость М (Н )в каждой точке кривой намагничивания. При H=0
, к-рая характеризует зависимость М (Н )в каждой точке кривой намагничивания. При H=0  ФМ не равна нулю, а имеет значение
ФМ не равна нулю, а имеет значение  , её наз. начальной М. в. С увеличением Я М. в. ФМ растёт, достигая максимума
, её наз. начальной М. в. С увеличением Я М. в. ФМ растёт, достигая максимума  на крутом участке кривой намагничивания (в области Баркгаузена эффекта), и затем вновь уменьшается. При очень высоких значениях Я (или при темп-pax, не очень близких к Кюри точке М. в. ФМ становится столь же незначительной, как и обычных парамагнетиков (область пара-процесса). Вид кривой
на крутом участке кривой намагничивания (в области Баркгаузена эффекта), и затем вновь уменьшается. При очень высоких значениях Я (или при темп-pax, не очень близких к Кюри точке М. в. ФМ становится столь же незначительной, как и обычных парамагнетиков (область пара-процесса). Вид кривой  (кривая Столетова, рис.) обусловлен сложным механизмом намагничивания ФМ. Типичные значения
(кривая Столетова, рис.) обусловлен сложным механизмом намагничивания ФМ. Типичные значения  и
и  : для
: для  и
и  , для
, для  и
и  , для сплава пермаллой (50% Fe, 50% Ni)
, для сплава пермаллой (50% Fe, 50% Ni)  и
и  (в норм. условиях). Наряду с
(в норм. условиях). Наряду с  вводят также обратимую М. в. , причём существенно, что изменение
вводят также обратимую М. в. , причём существенно, что изменение  поля должно происходить в сторону его уменьшения от нач. значения
поля должно происходить в сторону его уменьшения от нач. значения  . Всегда
. Всегда  . Разность
. Разность  и
и  , достигающая максимума вблизи значений
, достигающая максимума вблизи значений  ( Н с— коэрцитивная сила), может быть принята за меру необратимости процессов намагничивания и размагничивания (меру гистерезиса магнитного).
( Н с— коэрцитивная сила), может быть принята за меру необратимости процессов намагничивания и размагничивания (меру гистерезиса магнитного).


 и высотой образующей
и высотой образующей  довольно небольшой, чтобы считать в пределах площадей
довольно небольшой, чтобы считать в пределах площадей 






 , а во втором — ниже. Это делает цикл гистерезиса уже цикла
, а во втором — ниже. Это делает цикл гистерезиса уже цикла 
 — магнитный поток через поверхность, натянутую на этот контур.
— магнитный поток через поверхность, натянутую на этот контур.



 продолжает соблюдаться.
продолжает соблюдаться. (в отсутствие электростатического поля)
(в отсутствие электростатического поля)
 индукционный ток направлен против основного тока.
индукционный ток направлен против основного тока. индукционный ток направлен в том же направлении, что и основной ток.
индукционный ток направлен в том же направлении, что и основной ток. .
. — сумма магнитных потоков через все витки, а L — уже индуктивность многовитковой катушки. Ψ называют потокосцеплением или полным магнитным потоком [4] . Коэффициент пропорциональности L иначе называется коэффициентом самоиндукции контура или просто индуктивностью [3] .
— сумма магнитных потоков через все витки, а L — уже индуктивность многовитковой катушки. Ψ называют потокосцеплением или полным магнитным потоком [4] . Коэффициент пропорциональности L иначе называется коэффициентом самоиндукции контура или просто индуктивностью [3] . .
. .
.




