Как находить отношение площадей треугольника (2 видео)

Подобные треугольники

Содержание

Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
Основные сведения об отношении площадей подобных треугольников
Понятие подобия треугольников
Теорема об отношении площадей подобных треугольников
Доказательство теоремы
Примеры решения задач
Задача для самостоятельной работы
Отношение площадей подобных треугольников
🌟 Видео

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:60. Отношение площадей подобных треугольниковСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

Свойства подобных треугольников

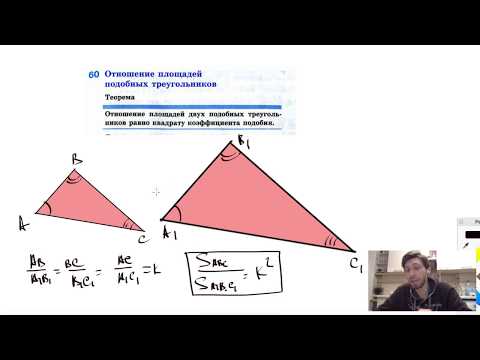
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Площади треугольников с равным углом.Скачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Отношение площадей треугольников с равным угломСкачать

Основные сведения об отношении площадей подобных треугольников

Видео:Отношение площадей треугольниковСкачать

Понятие подобия треугольников

Два треугольника называются подобными, если их углы попарно равны, а стороны, лежащие напротив соответственных углов пропорциональны.

A B / K L = B C / L M = A C / K M = k , ∠ A = ∠ K , ∠ B = ∠ L , ∠ C = ∠ M ⇒ Δ A B C

Отношение длин подобных треугольников называют коэффициентом подобия (k).

Также пропорциональные стороны подобных треугольников могут быть названы сходственными сторонами.

В подобных треугольниках, кроме сторон, подобны и другие величины: биссектрисы, медианы, высоты и т.д.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Теорема об отношении площадей подобных треугольников

Формулировка теоремы: отношение площадей подобных треугольников равно квадрату коэффициента подобия.

В геометрии существует три признака подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.

Свойства подобных треугольников:

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных элементов равно коэффициенту подобия.

Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Доказательство теоремы

Докажем теорему об отношении площадей подобных треугольников.

Теорема: отношение площадей подобных треугольников равно квадрату коэффициента подобия.

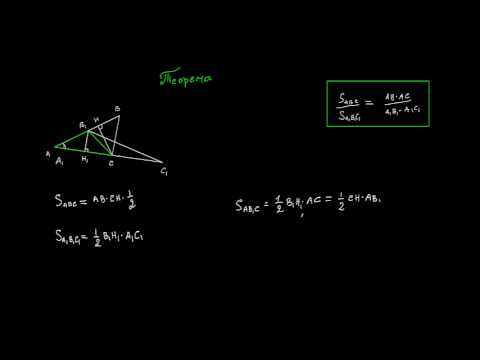
Доказательство: изобразим подобные треугольники Δ A B C

Из подобия треугольников по определению следует: A B / K L = B C / L M = A C / K M = k .

Воспользуемся следующей теоремой: если у двух треугольников равны углы (∠A=∠K), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем в виде формулы:

Что и требовалось доказать.

Видео:Отношение площадей подобных треугольников.Скачать

Примеры решения задач

Площади подобных треугольников ΔABC и ΔA1B1C1 равны соответственно 200 см² и 50 см². Сторона A1B1=5 см. Найдите сходственную ей сторону AB треугольника ABC.

По теореме об отношении площадей подобных треугольников: S a b c / S a 1 b 1 c 1 = k ² ⇒ 200 / 50 = k ² ⇒ k = 2 .

A B / A 1 B 1 = 2 , A B = A 1 B 1 * 2 , A B = 5 * 2 = 10 с м .

ΔABC и ΔA1B1C1 — подобны. Сходственные стороны AC и A1C1 соответственно равны 13 см и 0,1 м.

Найдите отношение периметров ΔABC и ΔA1B1C1.

A 1 C 1 = 0 , 1 м = 10 с м

A C / A 1 C 1 = 13 / 10 = 1 , 3 ⇒ P a b c / P a 1 b 1 c 1 = 1 , 3

Видео:Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Задача для самостоятельной работы

Треугольники Δ A B C

Δ K L M подобны. Площадь ΔABC равна 500 см², площадь ΔKLM равна 125 см². Сторона AC равна 18 см, найти сходственную ей сторону KM.

Проверьте, насколько верный или неверный ваш ответ.

Советуем составить краткий конспект для подготовки к уроку.

Видео:Отношение площадей подобных треугольников | Геометрия 7-9 класс #58 | ИнфоурокСкачать

Отношение площадей подобных треугольников

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»