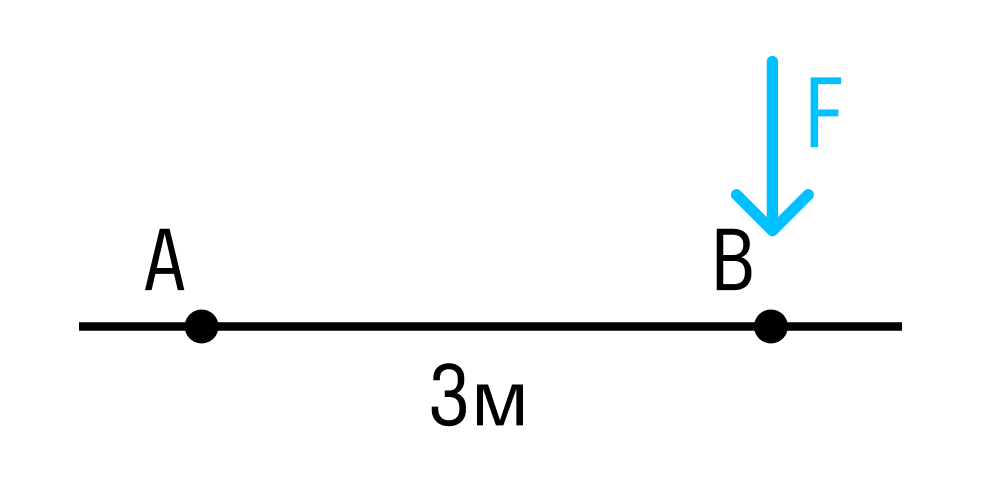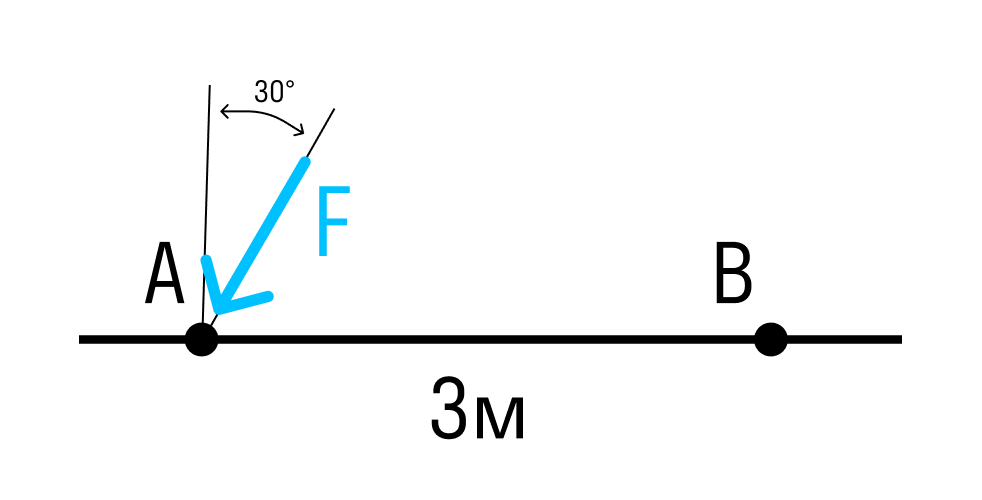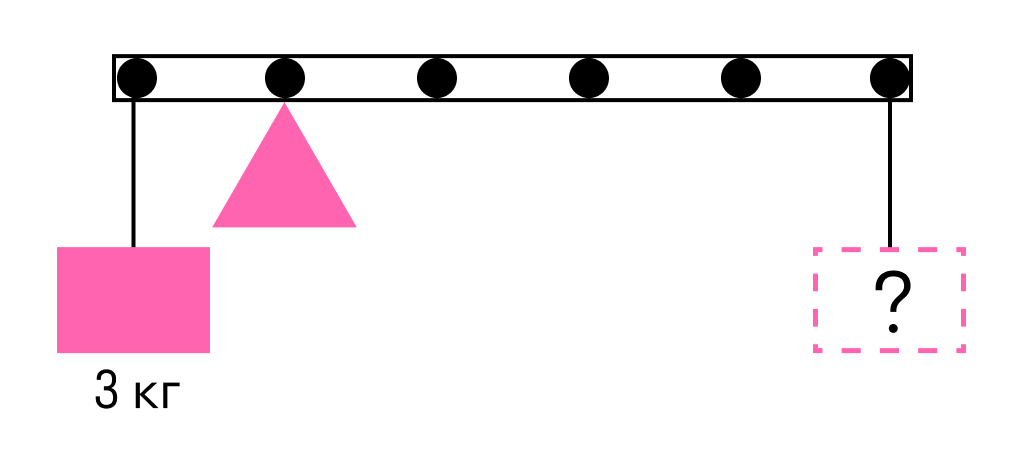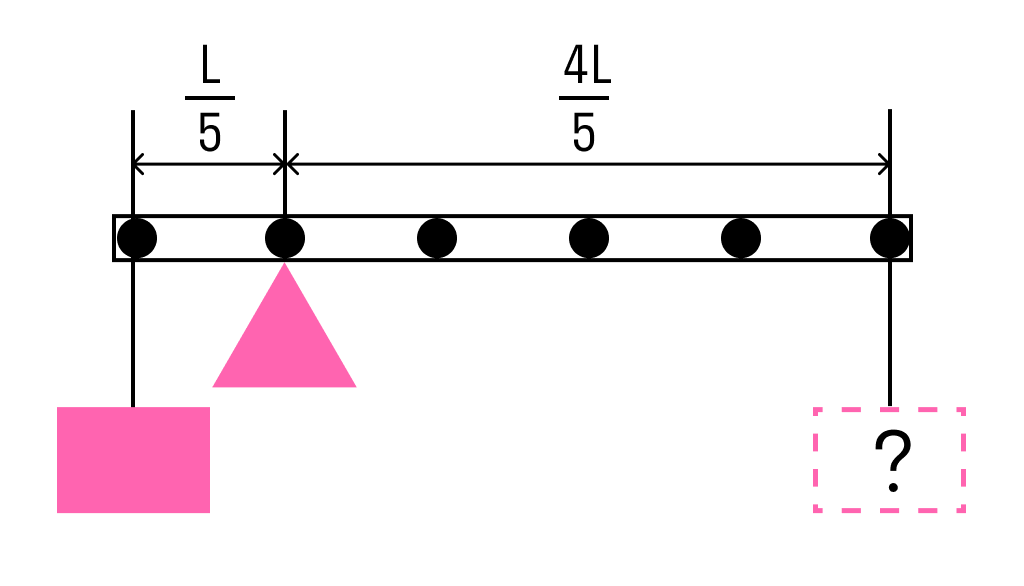Вектор нагрузки и рычаг силы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

• Сила — это физическая векторная величина, является мерой действия тела на другое тело.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Видео:Вектор нагрузки при приседаниях. Рычаг, плечо силы на рычаг.Скачать

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила —это плечо силы.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Видео:Закон рычагаСкачать

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Видео:Прикладная биомеханика #3: Отведение плечаСкачать

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.

Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.

На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.

Видео:Определяем направление силы в тренажерахСкачать

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

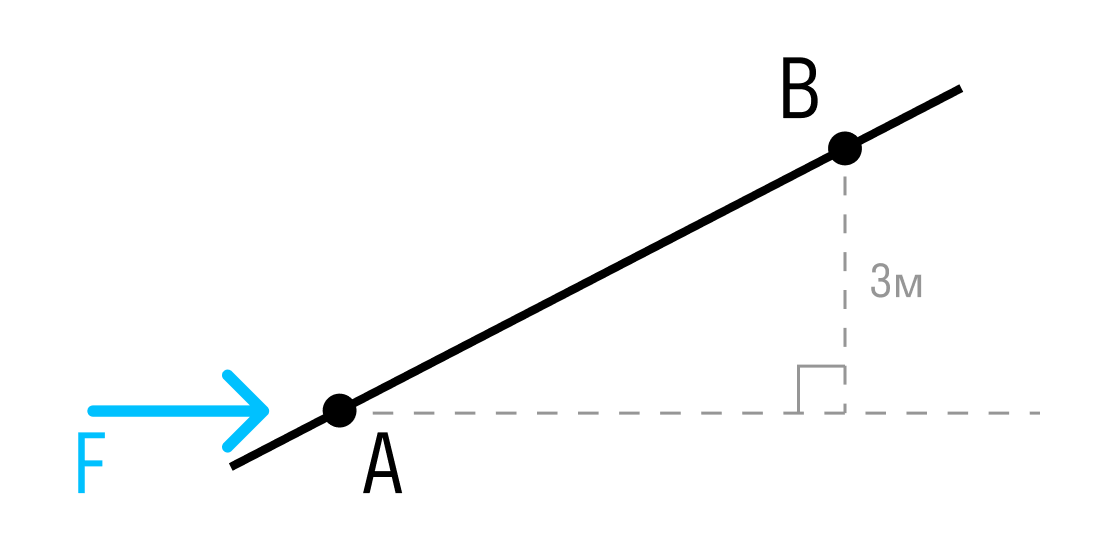
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

Видео:Учимся решать задачи по биомеханике, простой способ определить направление момента силы. #FPAСкачать

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M1 + M2 +. + Mn = M’1 + M’2 +. + M’n

M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

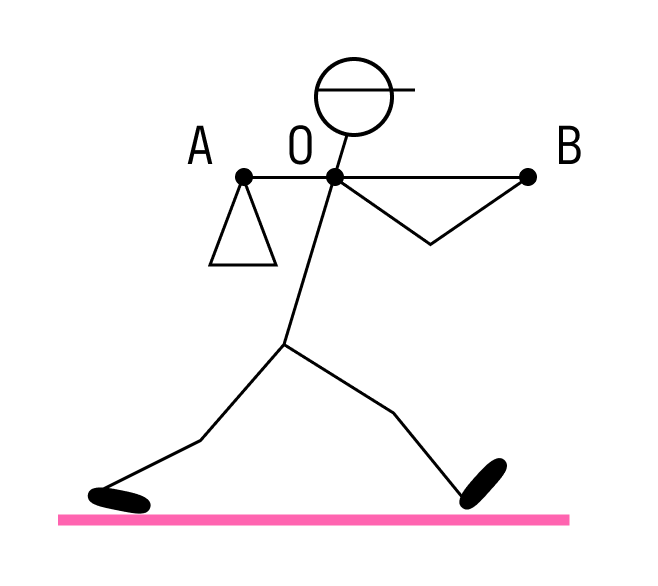
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

Ответ: расстояние ОА равно 30 см

Задача 3

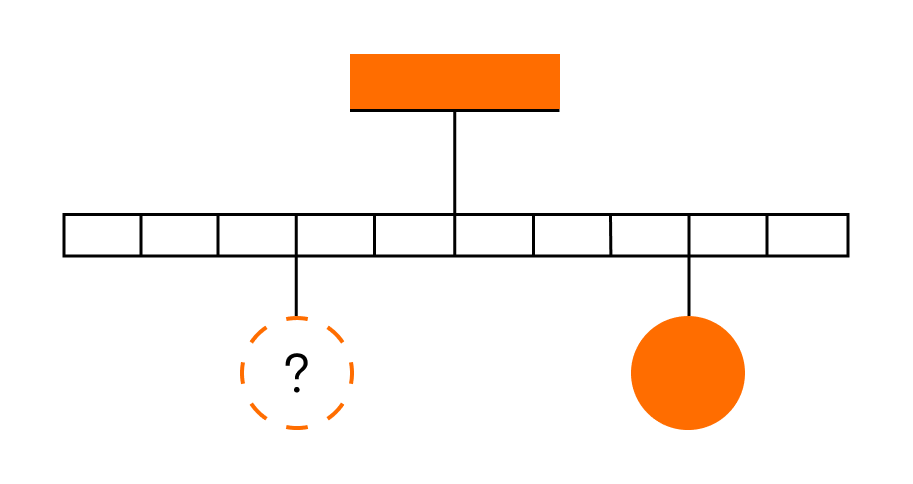
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

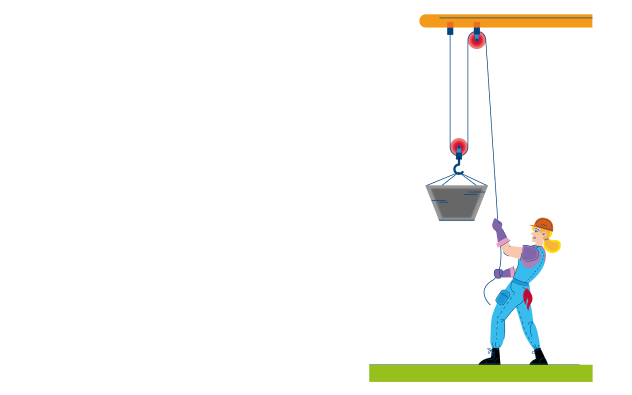
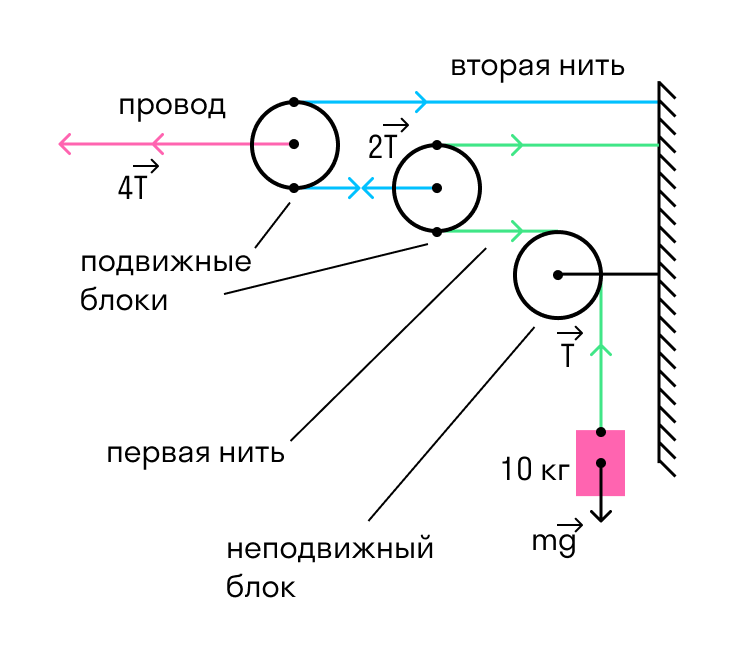
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Видео:РЫЧАГ МОМЕНТ СИЛЫ физика 7 класс ПерышкинСкачать

Момент силы

Содержание

Поговаривают, что древнейшим открытием и в какой-то степени самым первым научным достижением человека можно смело называть рычаг. Удивительно, но наши предки на уровне интуиции понимали, что увесистый камень намного проще поднять или передвинуть с помощью самой обычной палки, — при этом удивляет больше не наличие палки во всей этой истории, а осознание первобытным человеком принципа простых механизмов. Ведь палки первые разумные жители планеты специально искали подлиннее, понимая: чем длиннее, тем мне будет проще совершить работу.

«Катить проще, чем тянуть» — еще одно древнейшее «научное» открытие примитивного человека наряду с рычагом.

Принцип рычага передавался из уст в уста, от одного племени к другому, от одного поколения к следующему, словно элемент фольклора. Мы не знали, почему это работает, какое отношение к этому имеет наука физика. Более того, мы и слова-то такого не знали — «физика». У нас не было формул, не было определений, не было следствий из этих определений. Был лишь рычаг в самых его разных формах проявления и четкое знание — возьмись подальше от точки опоры, если тяжело.

И лишь в третьем веке до нашей эры, к моменту, когда рычаговые механизмы успели стать прочной основой нашей жизнедеятельности, Архимед впервые произвел необходимые математические расчеты и наконец описал теорию рычага, которой мы пользуемся и по сей день. Он первым связал друг с другом понятия груза, плеча и силы, и, как гласит легенда, осознав масштабы своего открытия, воскликнул: «Дайте мне точку опоры, и я переверну Землю!»

Благодаря опытам Архимеда, его фундаментальному пониманию закона равновесия рычага, впоследствии возникла крайне важная физическая величина — момент силы.

Видео:Момент силыСкачать

Закон равновесия: опыт с грузами

Определить момент силы можно как следствие закона сохранения энергии, как следствие второго закона Ньютона, также можно определить его методами векторной алгебры, однако чтобы не просто определить, но понять, что скрывается за данной величиной, не нужно применять пока нам незнакомые понятия — достаточно вспомнить условие равновесия рычага и провести несложный опыт с подвешенными грузами.

Опыт с грузами, рис. 1. Простая система из линейки, балки, крепления и крючков.

Во-первых, возьмем небольшую деревянную балку и к ее верхнему концу прикрепим болтом мерную линейку таким образом, чтобы крепление располагалось в центре тяжести линейки. Далее к линейке прикрепим по сантиметровым делениям несколько крючков, за которые будем подвешивать грузики разной массы. Начнем с отметок $10$ и $20$ — по пять сантиметровых делений влево и вправо от центра тяжести в $15

Опыт с грузами, рис. 2. Справа от точки опоры рычага подвешиваем первый грузик массой $20

Теперь возьмем грузик массой $40

г$ и для примера так же подвесим его за крючок, располагающийся на расстоянии $5

см$, только с другой стороны. Очевидно, что рычаг в результате не окажется в положении равновесия: с левой стороны, где висит сорокаграммовый грузик, на плечо рычага действует бó‎льшая сила $mvec$.

Опыт с грузами, рис. 3. Отклонение рычага в левую сторону при подвешивании второго грузика массой $40

Интуитивно мы понимаем, что дабы добиться равновесия данной системы, один из грузиков нужно куда-то сместить. Мы так же интуитивно понимаем, что если смещать грузик массой $40

г$, его нужно подвесить за крючок, располагающийся ближе к точке опоры. Смещать грузик массой $20

г$ нужно в другую сторону — подальше от точки опоры.

Вопрос на миллион: если, скажем, мы хотим перевесить двадцатиграммовый грузик, на сколько делений должно увеличиться плечо груза?

Опыт с грузами, рис. 4. Рычаг в положении равновесия.

Стандартным методом проб и ошибок, перевешивая крючок с грузиком по разным отметкам на линейке, можно со временем обнаружить, что рычаг придет в положение равновесия, если двадцатиграммовый грузик подвесить на расстоянии десяти сантиметров от точки опоры — на отметке $25

см$. Обратите внимание на то, как пропорциональны получаемые величины: грузики массой $40

г$ уравновешивают друг друга на плечах длиной $5

Видео:ЭТОТ ВИД НАГРУЗКИ УСКОРЯЕТ РОСТ МЫШЦ в 2 РАЗАСкачать

Условие равновесия

Именно таким образом, исключительно эмпирически, то есть опытным путем, Архимедом было сформулировано условие равновесия рычага. Можно долго перевешивать грузики, пользоваться различными массами, рычагами короткими, рычагами длинными, но одна вещь всегда будет объединять все элементы и переменные:

Рычаг находится в положении равновесия при условии, что отношение масс, подвешенных грузов, будет обратно пропорционально отношению расстояний от точки опоры до центров тяжести грузов.

Математически записать можно следующим образом:

где $m_1$ — масса первого груза, $m_2$ — масса второго груза, $l_2$ — расстояние от точки опоры до центра тяжести второго груза, $l_1$ — расстояние от точки опоры до центра тяжести первого груза.

Однако подобное определение, как и полученная нами формула, годится разве что для физики уровня III век до н. э. Масса — понятие не универсальное, «расстояние от точки опоры до центра тяжести» звучит размыто и в ряде неочевидных по устройству рычаговых систем может вызывать больше вопросов, чем ответов. Что, если мы хотим дополнительно надавить на грузик? Как учесть это в формуле? А что, если под рычагом мы понимаем гаечный ключ? К нему прикладывается сила. Считать, сколько килограммов человек прилагает к ключу, чтобы он пришел в движение? Да уж: ненаучно, странно и расплывчато.

Если от масс перейти к силам, чтобы внести универсальности, и учесть, что на подвешенные грузики действует только одна сила — сила тяжести $mvec$, а вместо расстояний взять уже знакомое нам определение, связанное с силой — плечо силы, формулу можно улучшить до следующего вида:

Лучше, но все равно не то. Где гарантии, что на наш абстрактный грузик будет действовать только сила тяжести? Возвращаясь к вопросу о том, что на грузик можно надавить, причем не обязательно параллельно направлению вектора силы тяжести — сделать это можно под углом. Формула равновесия должна учитывать силы в общем и целом. Так что улучшим пропорцию еще раз и придем к окончательному математическому выражению условия равновесия:

где $F_1$ и $F_2$ — силы, действующие на рычаг, $l_1$ и $l_2$ — плечи сил.

Рычаг находится в положении равновесия, когда отношение сил, действующих на рычаг, обратно пропорционально отношению плеч этих сил.

Вот это уже определение универсальное: оно охватывает и наш частный случай с силой тяжести, и более комплексные системы в том числе. А теперь заметим, что согласно основному свойству пропорции из формулы выше получается следующее равенство:

$$F_1cdot l_1 = F_2cdot l_2$$

Ранее мы с подобным не сталкивались — с произведением силы на плечо силы. Именно это произведение и именуется в физике моментом силы.

Видео:Статика. Что такое плечо силы?Скачать

Определение момента силы

Формально момент силы определяется так:

Момент силы — физическая величина, характеризующая действие силы. Равняется произведению модуля силы на ее плечо.

В физике момент силы обозначается заглавной латинской литерой $M$ и измеряется в $Н cdot м$ — в ньютонах на метр. Характеризует момент силы, как мы указали в определении, действие силы. Но только что бы это могло значить и как бы это можно было понять?

Рисунок 5. Опыт с гаечным ключом. Обратите внимание на направление момента силы $M$.

Возьмем гаечный ключ, ухватимся рукой за его конец и приложим некоторое усилие, чтобы провернуть гайку. Для сравнения перехватим гаечный ключ примерно до середины ручки и также попробуем приложить некоторое усилие. Во втором случае провернуть гайку будет сложнее, чем если бы мы держались за конец ручки инструмента.

Причина? Образуются разные величины момента силы!

И это все то же самое о том же самом. То, о чем мы рассуждали, когда затрагивали принцип простых механизмов, отдельно рычагов; когда говорили о механическом выигрыше. Просто мы не могли дать строгого определения происходящему. Выходит, что «проще выполнить работу», «затратить меньше усилий», «взяться подальше» и прочие относительно абстрактные фразы, которые мы использовали при рассмотрении простых механизмов, расшифровываются следующим образом: образуется бóльший момент силы.

Иными словами, момент силы — это и есть в своем роде величина усилия. Чем больше момент, тем быстрее двигается предмет, тем проще он проворачивается, тем легче выполняется действие. Говоря языком аналогий, плечо силы можно представить взлетной полосой, а момент силы — скоростью самолета. Если полоса длинная, самолет сможет развить бóльшую скорость и легко, как следствие, оторваться от земли.

Так что, да, момент и вправду характеризует действие силы. Характеризует, насколько это действие, скажем, активное, энергичное, полезное для нас в достижении некоего результата. Ведь сила по модулю может быть одинаковая, но за счет «разных длин взлетных полос», то есть плеч сил, она может образовывать разный момент.

Больше момента силы — проще, быстрее, легче, механически выгоднее.

Видео:Лекция "Основы биомеханики" Никитин А.В.Скачать

Как рассчитать момент силы

Момент силы всегда рассчитывается как произведение модуля силы на плечо силы по записанной нами ранее формуле $M = F cdot l$. Иногда определять приходится результирующий момент — когда на тело действует несколько разнонаправленных сил, однако подобные «превратности» нам встретятся в программе лишь через пару лет, когда мы начнем более основательно использовать понятие вектора. Единственная сложность, которая пока может встретиться на пути, — определение плеча силы.

Для примера возьмем нечто отвлеченное от привычных нам двуплечих рычагов — ясно, что внутри подобной механической системы плечо силы чаще всего будет совпадать с плечом рычага, так что сложности как таковой с расчетом плеча силы не возникнет. Представим вместо этого, что мы раскручиваем прикрепленную к поверхности фигуру в форме трапеции. Ого!

Итак, наша вращающаяся трапеция. Силу мы прикладываем к концу фигуры — направление силы указано на изображении. Согласитесь, увидеть плечо силы для подобной схемы движения уже не так просто, особенно когда глаз привык к рычагам. Не паникуем и вспоминаем, что плечо силы есть перпендикуляр к линии действия силы, опущенный из точки опоры или, вернее сказать, из оси вращения. Подумайте, где на изображении находится ось вращения и по какой траектории проходит перпендикуляр.

Ответ: плечо силы будет равно длине отрезка $OA$. Ось вращения трапеции находится в точке $О$. Все гениальное просто, согласны?

Видео:Котика ударило током, 10 т. ВольтСкачать

Знак момента силы

Еще один немаловажный момент при расчете момента силы — знак величины. Момент может быть отрицательным или положительным, в зависимости от того, в каком направлении действует сила, приложенная к телу. Если она вращает тело по часовой стрелке, то момент силы считается положительным. Если наоборот — против часовой стрелки, то момент считается отрицательным.

Может ли момент быть нулевым? Конечно, почему нет. Логично предположить, что в случае, если плечо силы равно нулю, то сила не создает никакого момента. Например, если вы надавите на ось вращения, сдвинуть при таком приложении силы что-либо невозможно.

Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

Решение задачи на моменты

На данном этапе мы понимаем, что такое момент силы, как определять плечо силы и что момент, в зависимости от направления движения, может иметь отрицательное значение. С учетом главной формулы $M = F cdot l$ решим следующую задачу.

Условие. На земле лежит палка массой 20 кг и длиной 4 м. Палку приподнимают за конец, прикладывая усилие 120 Н. Какие моменты при этом создают силы, действующие на доску? Для простоты допустить, что моменты силы тяжести в поднятом положении палки и в вертикальном положении к земле равны.

Решение. Выполним следующие действия:

• Схематично зарисуем условия.
• Определим силы, действующие на доску.
• Определим ось вращения.
• Определим плечи сил.
• Рассчитаем моменты.

На палку действуют три силы: сила реакции опоры $vec$, сила тяжести $mvec$ и внешняя сила, которую мы прикладываем к концу, $vec$. Расположение сил и их направление изображено на рисунке. Ось вращения при этом располагается в точке $B$: мысленно представим, что палка совершает вращательное движение, описывает полный круг, а так как точка $B$ будет находиться в центре полученной окружности, она и будет считаться осью вращения.

Плечо силы реакции опоры $vec$ равно нулю, поскольку точка приложения силы и ось вращения совпадают. Следовательно, первый момент $M_N$ силы реакции опоры мы можем определить сразу без расчетов. Он равен нулю:

Далее опускаем перпендикуляр из оси вращения $B$ к внешней силе $vec$. Получаем, что плечо внешней силы $vec$ равно длине палки $d$:

По формуле $M = F cdot l$, зная, что по условию задачи длина палки составляет $4

м$, а модуль внешней силы равен $120

Н$, рассчитаем момент внешней силы $M_F$. Вращение происходит по часовой стрелке, следовательно, момент будет положительным по знаку.

Если допустить, что момент силы тяжести $M_$ в поднятом положении палки равен моменту в вертикальном положении к земле, то плечо силы тяжести $l_$ равно половине длины палки:

Примечание. Подобное допущение необходимо исключительно для простоты расчетов. Если бы пришлось определять плечо силы тяжести «честно», в задаче также должны фигурировать как минимум высота подъема палки и угол подъема. Для вычисления плеча в треугольнике понадобились бы теорема косинусов и геометрические признаки подобия треугольников. Да-да, это вообще что за термины такие? Поэтому считаем «нечестно», в лежачем положении. Нахождением сложных плеч вы будете заниматься в курсе статики для 10 класса.

Теперь рассчитаем момент силы тяжести $M_$ по формуле моментов, учитывая, что движение происходит против часовой стрелки. Момент отрицательный:

$$M_=-fraccdot mgcdot l_=-0.5 cdot 20 cdot 9.8 cdot 2 =-196

Ответ: $M_N=0, M_F=480

Видео:Рычаг. Урок №1Скачать

Правило моментов

Остается последнее — разобраться, зачем нужно отрицательное значение момента силы.

Ранее мы говорили о том, что условием равновесия рычага является обратная пропорциональность отношений сил к плечам этих сил. Однако условие равновесия можно задать и через смежное понятие момента силы, что в некоторых случаях даже удобнее для вычислений.

Вернемся к нашей вращающейся трапеции. Представим, что вы стоите и прикладываете к одному концу трапеции силу $vec_1$, а внезапно появившийся из ниоткуда ваш друг увидел, как вы играетесь с фигуркой и решил тоже во всем этом поучаствовать. Он берется за другой конец трапеции и тянет фигурку в противоположную сторону c силой $vec_2$. Вы в одну сторону, он в другую, при этом трапеция вращаться никуда не хочет — она упрямо находится в положении равновесия. Но, казалось бы, моменты сил создаются. Где движение?

Дело в том, что один момент силы, условно говоря, «гасит» другой. Математически вычитается. Как только создаваемый вами момент силы превысит тот, что создается вашим другом, фигурка начнет движение по часовой стрелке, к вам. Если друг поднажмет, то трапеция пойдет против часовой стрелки, от вас.

Таким образом, мы можем складывать все моменты, действующие на тело, чтобы понимать, движется ли тело, и если да, то в какую сторону. Знак числа — удобный математический инструмент, позволяющий работать с направлениями. Если сумма всех моментов положительна, вращательное движение идет по часовой стрелке. Если отрицательна — против часовой.

А если сумма моментов равна нулю?

Логично, что тогда тело находится в положении равновесия. Оно не двигается. Вот как мы можем получить условие равновесия (неважно — рычага или другого тела), выраженное через момент силы.

$$sum_i M_i= M_1+M_2+…+M_i =0$$

Подобное равенство называется правилом моментов:

Правило моментов: тело находится в состоянии покоя, если алгебраическая сумма всех моментов сил, приложенных к телу, равняется нулю.

Видео:Стрим с профессором. Биомеханика жима и приседа. Особенности включения мышц и их работыСкачать

Приседания со штангой. Взгляд изнутри [Часть 1]

Низкий поклон, наши уважаемые читатели! В эту пятницу мы продолжим наполнение цикла “Вектор силы” и остановимся на упражнении приседания со штангой.

По прочтении Вы узнаете, какие силы и моменты возникают во время выполнения движения, к каким частям тела приседания предъявляет повышенные требования, а также мы разберем некоторую исследовательскую сторону. Не факт, что все осилим в одной части и тогда разобьем на две.

Итак, рассаживайтесь поудобней, мы начинаем.

Видео:ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать

Приседания со штангой: векторы, силы, моменты

Кто бы мог подумать, что наш новый и достаточно сложный для восприятия цикл придется Вам по вкусу. Конечно, еще рано делать окончательные выводы (так мы их не делаем :)) , но предварительно уже можно сказать, что да, цикл приживается и весьма неплохо. Нашу первую заметку мы посвятили жиму штанги лежа, во второй поговорим про приседания со штангой. Вообще, стоит сказать, что именно это упражнение является самыми технически сложным и травмоопасным. И чтобы получать от приседа максимальную пользу, желательно взглянуть на него со стороны, а точнее — изнутри. Этим самым действом мы сегодня и займемся.

Примечание:
Для лучшего усвоения материала все дальнейшее повествование будет разбито на подглавы.

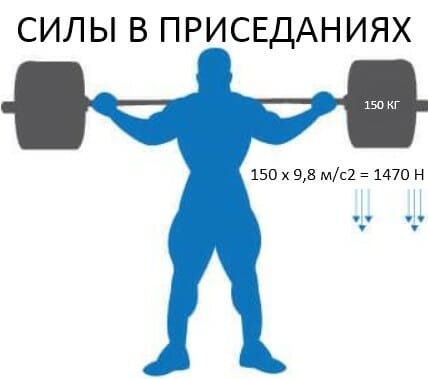
Приседания со штангой: силы

F=[m]х[a] – такова формула силы, рассчитываемой в Ньютонах. 1 H — это сила, необходимая для ускорения 1 кг массы со скоростью 1 м/сек2. Если Вы решили приседать и снарядили штангу весом 150 кг (массовая составляющая силы) , то она будет прилагать 150х9,8 м / сек2 = 1470 Н силы на Ваше тело. Чтобы переместить вес вверх, Вам нужно преодолеть 1470 Н силы.

Чем больше вес, тем больше прилагаемая сила, тем бОльшую перегрузку испытывают Ваши “элементы” тела. Поэтому, с точки зрения сохранности организма и долголетия в спорте, более щадящим вариантом являются приседания с гантелями.

С точки зрения биомеханики силы в суставах и на различных костях отличаются. Разные стойки (в т.ч. положение грифа на трапециях) или захваты штанги (уже, шире) могут сделать приседания более легкими или сложными.

Приседания со штангой: моменты

Момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага (в случае если сила приложена к рычагу перпендикулярно) . Для понимания рассмотрим практический пример из жизни.

Вам нужно с помощью гаечного ключа завернуть болт. В таком случае момент силы будет представлять собой следующую картину:

Что касается непосредственно самих приседаний, то, чтобы осуществить движение, мышцы сокращаются, производя линейную силу. С точки зрения моментов Вы в первую очередь пытаетесь создать экстензорные моменты (разгибания) в коленных суставах и бедрах, которые превышают флексорные моменты (сгибания) в этих суставах, налагаемые как весом штанги, так и собственным весом тела. Если атлет генерирует достаточную силу, которая превышает силу, оказываемую штангой на его тело, то он успешно выполняет приседания.

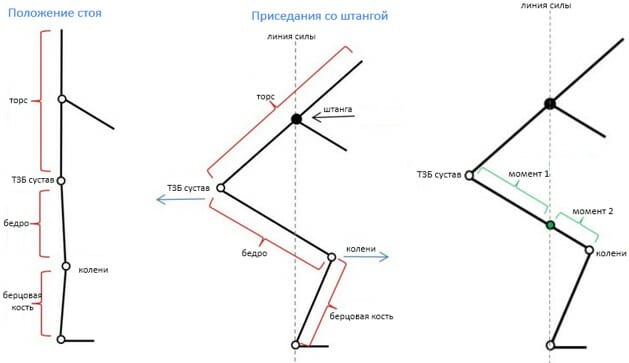
Если рассмотреть (наглядно) приседания с точки зрения моментов/сил, то когда штанга загружается на спину, центр масс падает на ноги, создавая так называемую линию силы. Именно по этой линии все и будет происходить:

Во время приседаний колено будет двигаться вперед, так как бедра будут двигаться назад. Как только колено продвигается вперед (мимо линии силы) , возникает момент, то же самое верно для бедер. Сгенерированный момент представляет собой вес штанги, умноженный на расстояние колена (или бедра) от силовой линии.

Подытоживая все сказанное, выведем несколько силовых положений по приседаниям со штангой:

• в приседаниях нагрузка (штанга + вес тела) применяет направленную вниз силу, которая оказывает внешние сгибательные моменты на колени, бедра и внешний момент дорсифлексии (движение, которое мы совершаем, когда, стоя на пятках, отрываем от пола подушечки под пальцами ног) по отношению к лодыжке;
• величина внешнего сгибающего момента, который Вы должны преодолеть, чтобы поднять вес, зависит от двух факторов: самой нагрузки и плеча силы. Обычно люди с короткими конечностями (особенно низа) прогрессируют (по весу) в приседаниях быстрее, чем их длинноконечностные коллеги;
• всего два фактора, которые определяют то, могут ли Ваши мышцы создавать достаточно большие внутренние моменты разгибания, чтобы поднять нагрузку — точки крепления мышц и сила, с которой они могут сокращаться;
• Вы не можете изменить точки прикрепления мышц, поэтому единственным фактором, находящимся в Вашем распоряжении, является увеличение сократительной силы. Два способа делают это: 1) повышение мастерства в приседаниях, чтобы текущая мышечная масса генерировала больше силы во время выполнения движения, 2) увеличение количества мышц (гипертрофия + гиперплазия).

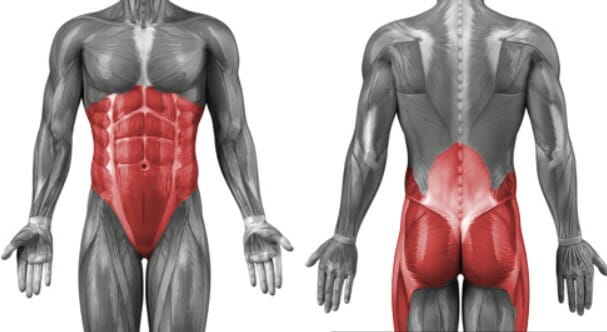
Приседания со штангой: кости, суставы и мышцы, играющие наиболее важную роль в выталкивании веса

Далее по тексту мы разберем некоторые анатомические вопросы, а именно выясним, к каким “элементам” тела приседания предъявляют повышенные требования.

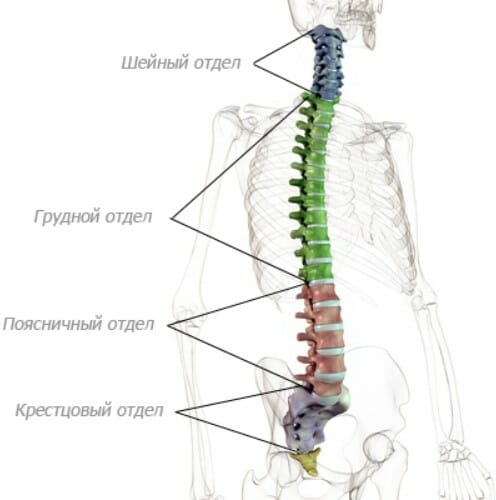
№1. Позвоночник

Спинной хребет, образуемый цепью костей/хрящей (24 позвонка) , идущих вдоль спины и заключающих в себе спинной мозг. Позвонки поделены на три отдела: 7 шейных позвонков на шее, 12 грудных позвонков, идущих от основания шеи до нижней части грудной клетки и 5 поясничных позвонков, идущих от основания грудной клетки к верхней части таза.

У позвоночника есть три основные кривые: лордотическая кривая (округленная внутрь) для поясничного отдела позвоночника, кифотическая кривая (округленная наружу) для грудного отдела позвоночника и лордотическая кривая для шейного отдела позвоночника.

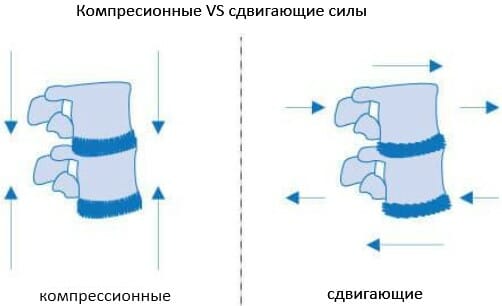
Между каждой парой позвонков есть межпозвоночный диск, который выполняет амортизирующие функции. Они (диски) очень хорошо выдерживают сжимающие силы/компрессионные нагрузки (прижимая друг к другу позвонки вместе в результате воздействия нагрузки, возникновения сдавливающего усилия) , но могут иметь некоторые проблемы со сдвиговыми/поперечными усилиями.

В правильном исполнении приседаний, когда верно поставлена спина, не должно быть избыточного количества флексии или экстензии (сгибание/разгибание) позвоночника. Только так спина сможет переносить силу с ног/бедер на гриф.

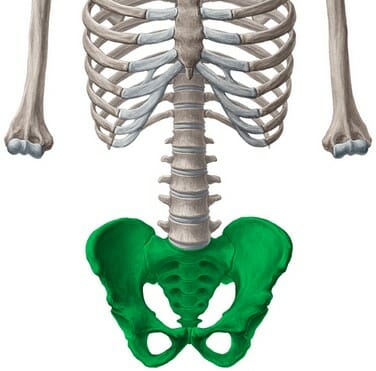
№2. Таз

Таз представляет собой шесть костей, слитых воедино. Тазовые кости несут на себе ягодичные мышцы, которые принимают на себя нагрузку от приседаний. У таза, в ключе наших изысканий, есть две особенности: 1) имеется передний нижний подвздошный позвонок/ость, из которого берет свое начало квадрицепс (4 мышцы передней поверхности бедра) ; 2) имеется ишиальная бугристость, из которой берут свое начало бицепсы бедер и большая приводящая мышца.

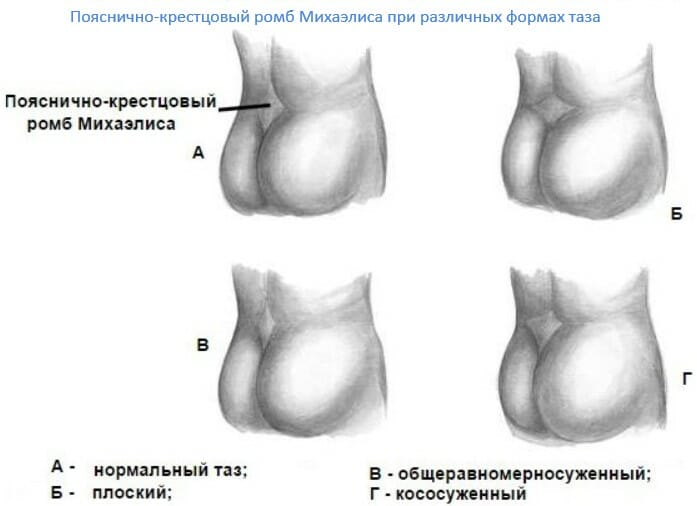
Женский таз (не у всех) анатомически более расширен в сравнении с мужским, что на практике, т.е. в отношении приседаний, должно выливаться в формирование более устойчивой опоры. Т.е. женщинам с расширенным тазом приседать будет проще (в плане устойчивости, жесткости конструкции) , чем их “узкотазым” коллегам женщинам или мужчинам.

В зависимости от того, какой у женщины таз, её пояснично-крестцовый ромб (ромб Михаэлиса) будет иметь разный вид:

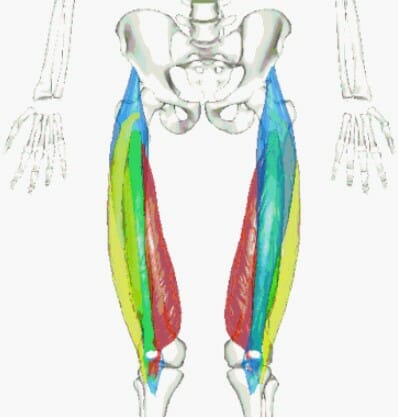
№3. Бедренная кость

Бедренная кость – кость, простирающаяся от точки таза до колена. Есть четыре основные части бедренной кости: головка, шейка, ствол и мыщелки.

Перелом шейки бедра – наиболее частая проблема у женщин возраста 40+, активно занимающихся спортом (и не только) . Факторов такого развития событий множество. В ключе занятий силовым фитнесом — это частое выполнение приседаний и жимов ногами лежа с достаточным отягощением.

Вниз по ноге бедренная кость встречается с коленом, которое имеет 4 основные связки: передняя крестообразная связка (ACL) , задняя крестообразная связка (PCL) , медиальная коллатеральная связка (MCL) и латеральная коллатеральная связка (LCL) .

Бедра и колени (как связки, так и сами чашечки/мениски) во время приседаний испытывают колоссальные нагрузки. Поскольку у женщин кости более хрупкие, а коленные связки более слабые по сравнению с мужчинами, то их не стоит перегружать, выполнять соответствующие упражнения, в том числе и силовые приседания со штангой, чаще 1-2 раз в неделю.

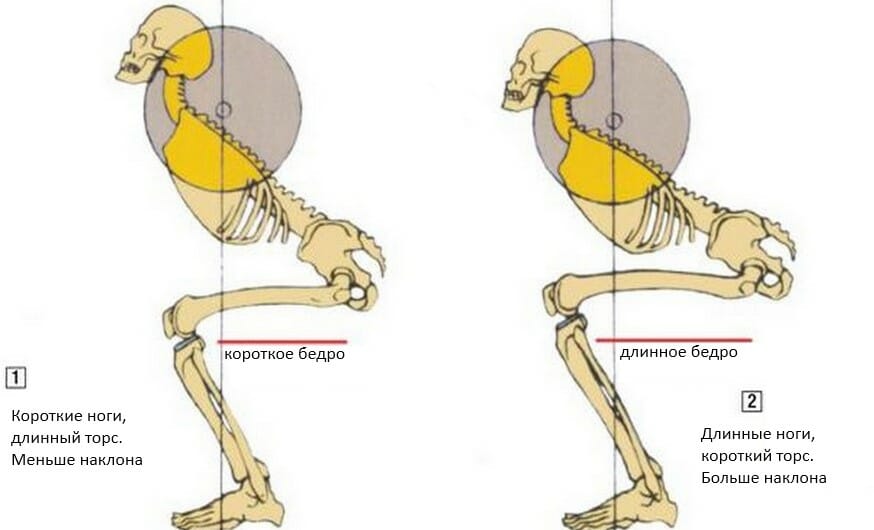
Стоит иметь ввиду, что длина бедренной кости накладывает существенный отпечаток на механику приседаний. Т.е. люди с разной длиной конечностей (в частности бедренной кости) должны приседать по-разному.

Что значит длинная бедренная кость? Это значит, что значение отношения “длина бедра к торсу” у Вас высокое/большое или высокое/большое соотношение бедренной к короткой большеберцовой кости.

Приседания с длинной бедренной костью могут привести к травме нижней части спины.

Итак, если Вы имеете длинную бедренную кость и короткий торс, то в приседаниях:

• используйте более широкую (чем обычные люди) постановку ног;
• направляйте бедра в стороны (внешнее вращение) ;
• подкладывайте под пятки блины.

Все указанные советы меняют рычаги и равномерно распределяют вес между нижней частью спины, коленями и ногами. Таким образом, никакой “элемент” не перегружен больше, чем другие.

№4. Тибия и Фибула

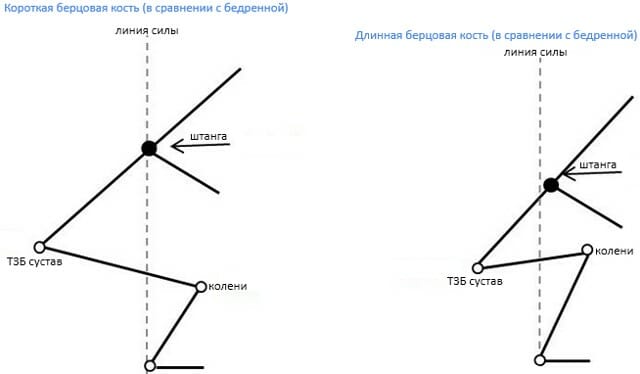
Большеберцовая и малоберцовая кости — кости низа ноги, простирающиеся от колена до лодыжки. Могут не вписываться по длине в анатомические стандарты, быть короче или длиннее. В таком случае механика приседаний также изменяется (отличается от классики) .

№5. Тазобедренный сустав

Бедро — это шарнирное соединение, что означает его движение во всех плоскостях. В приседаниях важен диапазон движения (чем больше, тем лучше) и на это влияют: анатомические особенности таза, тазобедренного сустава, бедренной кости, а также способности низа к растяжке (хороший отклик) . Именно это будет определять качество (в т.ч. глубину) Ваших приседаний.

№6. Коленный сустав

Является шарнирным соединением, что означает, что он в первую очередь выполняет сгибание (например, сгибание ног лежа в тренажере) и разгибание (например, разгибание ног в тренажере) . Коленная чашечка, маленькая косточка в передней части колена, усиливает рычаг квадрицепсов, чтобы вытащить большеберцовую кость для осуществления разгибания колена.

Коленный сустав у женщин много слабее, чем у мужчин, посему не рекомендуется в один день нагружать его тяжелыми приседаниями и другими упражнениями на разгибание/сгибание. С точки зрения долголетия коленей целесообразно использовать не более трех упражнений на них в тренировку, причем отстоящих друг от друга на одно любое другое движение. Пример: 1) разгибание ног сидя, 2) румынская тяга с гантелями, 3) приседания со штангой, 4) подъемы на носки стоя, 5) сгибание ног лежа.

№7. Лодыжка

Лодыжка может вращаться и изгибаться в стороны. В ключе приседаний для нас важно только подошвенное сгибание и дорсифлексия (отрыв подушечек пальцев от пола) . Хорошая подвижность лодыжки часто может компенсировать нестандартную анатомию человека и позволить правильно выполнить присед.

Теперь, подытоживая сказанное по суставам, давайте перенесем наш анатомический опус в практическую плоскость, т.е. посмотрим, как анатомия работает именно в приседаниях.

Правильно приседать это значит приседать в соответствии со своей антропометрией, длинной конечностей, пропорциями тела. Именно эти пропорции диктуют, какие мышцы будут забирать не себя бОльшую часть работы. Для некоторых присед будет работать как “качатель» квадрицепсов, для других — ягодиц, бицепсов бедер.

Далее в упрощенном схематичном виде приведем некоторые варианты движения всех узлов тела при выполнении приседаний в зависимости от исходных пропорций человека.

Если Ваша большеберцовая кость короче по сравнению с бедренной костью (рисунок 1) , Ваше тело будет диктовать наклоняться вперед, в то время как Ваши колени не могут идти вперед. Таки образом, большая часть нагрузки будет приходиться на низ спины, а не квадрицепсы. С другой стороны, если Ваша большеберцовая кость больше/длиннее Вашей бедренной кости (рисунок 2) , тогда Вы почувствуете большую нагрузку на колени, и приседания будут работать на квадрицепсы.

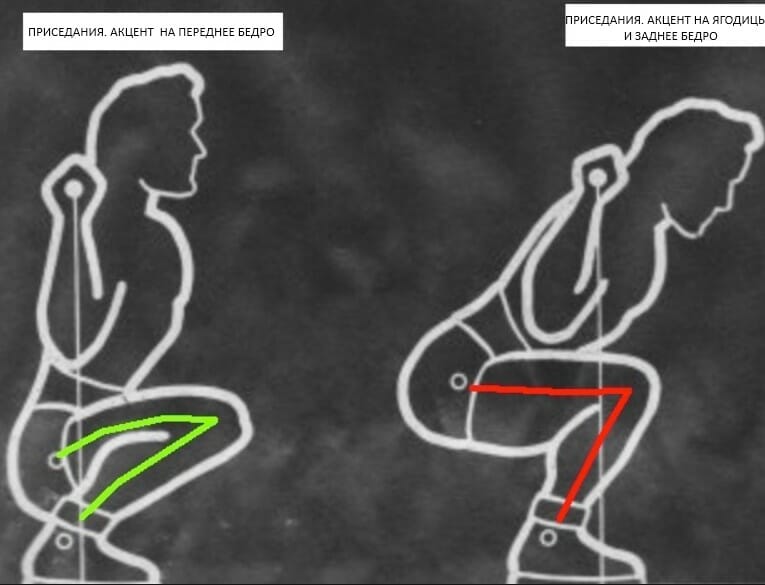
Если с костями в плане длины у Вас все в порядке, т.е. они находятся в некой пропорции м/у собой (одна не разительно больше/меньше другой) , то приседания тоже можно настроить на проработку той или иной части ног. Например, чем дальше колено продвигается вперед (глубже присед, попа в пол) , тем бОльшая нагрузка приходится на переднее бедро, качается квадрицепс (также больше веса будет влиять на Ваши коленные суставы, подколенные связки) . И наоборот, если Ваше колено продвигается вперед лишь на небольшое расстояние (небольшая глубина приседа) , то Ваши задние бедра и спина возьмут на себя бОльшую часть нагрузки (качается бицепс бедра, ягодицы) .

Теперь пройдемся по мускулатуре.

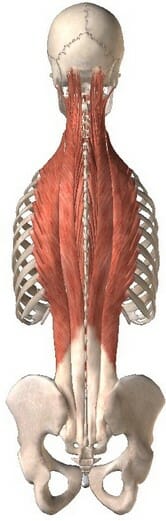
№1. Разгибатели спины

Прикрепляются к верхней части таза, ребрам и позвоночнику, и когда они сокращаются, происходит разгибание позвоночника. Каждая отдельная мышца пересекает только несколько позвонков, поэтому необходимо отслеживать силу каждого региона спины. Другими словами, дружба с приседаниями начинается с улыбки укрепления и развития верха, середины, низа спины.

№2. Мышцы кора

Это общий термин для всех мышц между шеей и бедрами, которые помогают поддерживать туловище, отвечают за стабилизацию таза, бедер и позвоночника и формируют жесткий опоясывающий живот корсет. К мышцам кора относятся (основные) :

• косые мышцы живота;
• поперечная мышца живота;
• прямая мышца живота малые;
• средние ягодичные мышцы;
• приводящие мышцы;
• мышцы задней поверхности бедра;
• подостная мышца;
• клювовидно-плечевая мышца.

Важна развитость именно комплекса (а не отдельно взятой) мышц. Они должны быть способны создавать достаточное напряжение, чтобы оказывать поддержку разгибателям спины в поддержании и стабилизации позвоночника. Косая, поперечная и прямая мышцы помогают диафрагме и мышцам тазового дна в создании и контроле внутрибрюшного давления.

Чем больше вес в приседаниях, тем сильнее должен быть пресс и мышцы кора. Т.е. условно, если Вы приседали с весом 50 кг и хотите поднять его до 75, ноги это могут позволить сделать, но пресс не в полной мере. Используйте в упражнениях на пресс дополнительные отягощения (например, блины) и увеличивайте время стояния в планке (минимум 90 сек для женщин и 180 сек для мужчин) .

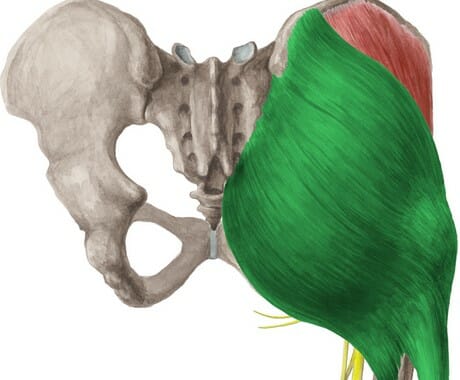
№3. Большая ягодичная

Gluteus maximus это самый сильный разгибатель тазобедренного сустава. Крупные мощные ягодицы крайне важны для выполнения приседаний. Многие барышни придя в зал сразу начинают качать ягодицы, залезая в присед — это в корне неверно. Развивая через специальные целевые упражнения ягодицы, мы помогаем себе в приседаниях. В приседаниях важна массовая составляющая силы (вес штанги) , 10-15 кг не заставят Ваши ягодицы расти. А чтобы поднимать серьезные веса, нужно довести все движители (в т.ч. ягодицы) приседаний до нужных силовых и массовых кондиций.

Вывод: развитость большой ягодичной мышцы важна в приседаниях со штангой, но она не нарабатывается ими.

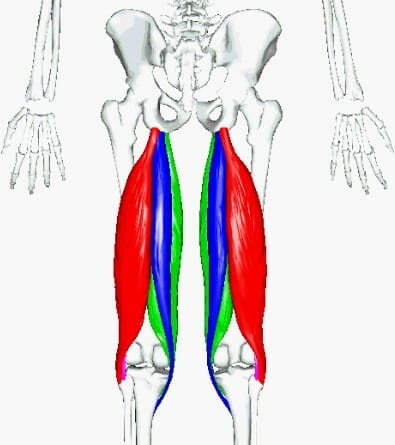
№4. Задняя поверхность бедра

Три основные мышцы, ее образующие – бицепс бедра (две головки) , полусухожильная и полуперепончатая. Решающее значения из всех трех в приседаниях имеет бицепс бедра, причем длинная головка. От ее силы и развитости зависит легкость преодоления фазы разгибания (выход наверх из нижней точки) . Самым простым упражнением локального воздействия являются сгибания ног стоя и лежа.

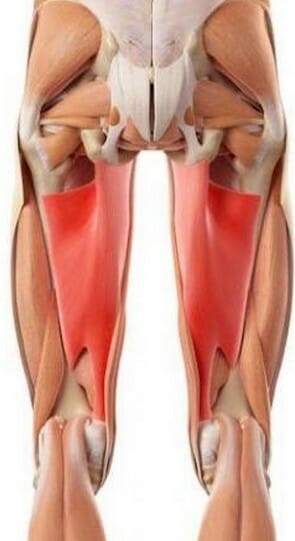
№5. Большая приводящая

Из всех аддукторов самым важным является adductor magnus, часто называемый четвертое подколенное сухожилие. Он является мощным разгибателем тазобедренного сустава. В большинстве своем, когда дело касается подтягивания под приседания отстающих мышц, речь идет о ягодицах и бицепсах бедер. Однако, согласно последним научным исследованиям (Andrew Vigotsky, Megan Bryanton, American Society of Biomechanics 40th Annual Meeting, At North Carolina State University, США 2016) бОльшим потенциалом разгибания (производит бОльший момент) тазобедренного сустава обладает большая приводящая мышца.

Вывод: чтобы эффективней выходить из нижней точки приседа прорабатывайте мышцы ног в такой последовательности (первая позиция – самые значимые) : 1) большая приводящая, 2) ягодицы, 3) бицепс бедра.

№6. Квадрицепс

Четырехглавая мышца бедра – одна из самых крупных мышечных групп ног. Мощные квадрицепсы позволяют осуществлять как “прием” веса штанги, так и проводить его мощный вынос на верх (фаза разгибания) . В зависимости от постановки ног в приседаниях можно сместить акцент на ту или иную головку/часть квадрицепса. Самым простым упражнением для развития переднего бедра является разгибание ног сидя в тренажере. Меняя положение стоп и носков, можно охватить разные его головки.

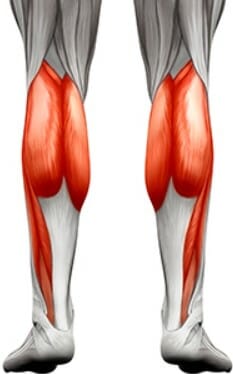
№7. Мышцы голени

Икроножные и камбаловидные мышцы выполняют роль подошвенных сгибателей и “вставляются” в пятку через ахиллово сухожилие. В тренажерном сообществе новичков (и не только) бытует мнение, что голень качать совсем не обязательно, т.к. эти мышцы находятся в постоянной работе, поскольку человек активно ходит. Это не так — прорабатывать эти мышцы нужно, особенно девушкам, любящим каблуки. Все дело в том, что обувь с каблуком более 3 см повышает нагрузку на носки (при высоте каблука 6 см около 70-75% веса тела приходится на передний отдел стопы) . Частое их ношение приводит к эквинусу – невозможности без болей разогнуть стопу. В приседаниях важна устойчивость и подошвенная гибкость, сильные мышцы голени помогают выталкивать тело наверх. Женщины, которые носят на работе каблуки и ходят в зал, по указанным двум пунктам находятся “в пролете” – у них не гибкая стопа, а в голени нарушена микроциркуляция крови.

Вывод: развитые икроножные и камбаловидные мышцы оказывают существенную поддержку мышцам ног в преодолении мертвой точки в приседаниях.

Собственно, анатомическую часть наконец-таки разобрали.

Ауууу! Вы еще тут? Или я сотрясаю воздух вхолостую? 🙂

Если помните, в начале статьи высказывалось предположение, что повествование может затянуться. Так оно и случилось. 2600 слов, а мы только в одном глазу. Посему предлагаю перенести оставшееся во вторую часть и таки добить в следующую пятницу. Вы как — за? Молчание — знак согласия, так и поступим!

Послесловие

Приседания со штангой открыли наш новый цикл “Вектор силы” и мы посмотрели на них изнутри. Правда, пока не до конца, но обстоятельно. Продолжим уже совсем скоро, ждем-с!

PPS: Друзья, вторая заметка понятней первой или еще хуже :)?

С уважением и признательностью, Протасов Дмитрий.

🎬 Видео

Крутящий момент. Что это такое и зависит ли от мощности?Скачать

Равнодействующая и сложение силСкачать

Болевые точки анатомии и биомеханики | Дмитрий КалашниковСкачать

Зачет по биомеханике ФПА, часть 2Скачать