Вектор и матрица корреляций

В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.

В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.

Видео:Корреляция и ковариация двумерной случайной величиныСкачать

7. Векторизация и нормирование одномерных координат

Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений

и строим новый набор как разность между исходными числами и их центроидом (средним):

Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):

Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:

Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).

Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.

Упражнение для тех, кто любит «щупать руками». Построить ССК для набора .

Видео:Матрицы и векторыСкачать

8. Векторизация и ортонормирование многомерных координат

Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.

Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики . Обращаем внимание, что второй индекс — это номер характеристики (столбцы матрицы), а первый индекс — номер точки (элемента) набора (строки матрицы).

Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:

Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?

Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).

Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.

Умножая МКВ на транспонированную, мы получаем матрицу корреляции:

Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).

Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):

Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.

Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.

Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).

Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.

Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.

Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

9. Матрица Грина — это матрица корреляции векторов

Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?

Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.

Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний

в формулу преобразования девиации:

Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):

Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):

Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.

Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).

Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.

Видео:Что такое векторы и матрицы? Душкин объяснитСкачать

Расчет значений вектора и матрицы корреляции

В разд. 1.3 отмечалось, что для оценивания силы линейной зависимости объясняемой переменной у от потенциальных объясняющих переменных х_ь х₂, . х_т рассчитываются коэффициенты корреляции по формуле (1.19), которые формируют вектор корреляции R₀:

Также рассчитываются коэффициенты корреляции между потенциальными объясняющими переменными х_и х₂, . х_т по формуле (1.21)

а их значения записываются в виде матрицы корреляции R, симметричной относительно единичной диагонали.

Задание. Для представленного ниже множественного линейного уравнения и соответствующих ему данных следует оценить силы линейной зависимости объясняемой переменной у от потенциальных объясняющих переменных а также рассчитать коэффициенты корреляции между потенциальными объясняющими переменными х, и Xj, где i * j.

Расчеты следует выполнить по приведенным формулам, а затем с использованием функции КОРРЕЛ табличного процессора Excel и инструмента КОРРЕЛЯЦИЯ, входящего в пакет Анализ данных. Результаты расчетов необходимо представить в виде вектора R₀ и матрицы R корреляции.

А. Расчет коэффициентов корреляции по формулам (1.19) и (1.21).

Проведем расчет средних значений факторов:

Далее приведен пример расчета коэффициента корреляции между X] и у:

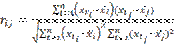
Рассчитаем далее r_yxl(rj):

Последующие расчеты коэффициентов корреляции между как у и Xj, так и Xj и Xj проведите самостоятельно.

В. Расчет коэффициентов корреляции с использованием функции КОРРЕЛ табличного процессора Excel.

Для расчета коэффициента корреляции г_уХ[ вызывается функция КОРРЕЛ и задаются в первом массиве значения из столбца у, а во втором массиве значения из столбцах!. Результат будет равен 0,631 (рис. 1.3).

Рис. 1.3. Задание аргументов функции КОРРЕЛ

Аналогичные действия необходимо повторить, меняя значения во втором массиве. Выполните эти действия самостоятельно и запишите полученные результаты в виде вектора корреляции R₀. После этого самостоятельно рассчитайте значения коэффициентов корреляции между х, и х₇ и запишите результаты в виде матрицы корреляции R.

С. Расчет коэффициентов корреляции с использованием инструмента КОРРЕЛЯЦИЯ пакета Анализ данных.

Для выполнения расчета вызывается инструмент КОРРЕЛЯЦИЯ, а в раздел Входные данные в окно Входной интервал вводятся все исходные данные с метками в первой строке. Ставится знак «V» в окне Метки в первой строке. Выполнив эти действия, следует указать параметры вывода (рис. 1.4):

Рис. 1.4. Задание моста вывода результата

Видео:Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

Роль вектора и матрицы корреляции множественной линейной модели при подборе объясняющих переменных

Объясняющие переменные в линейной эконометрической модели должны обладать следующими свойствами:

• иметь высокую вариабельность;

• быть сильно коррелированными с объясняемой переменной;

• быть слабо коррелированными между собой;

• быть сильно коррелированными с представляемыми ими другими переменными, не используемыми в качестве объясняющих*.

Объясняющие переменные подбираются с помощью статистических методов.

Процедура подбора переменных состоит из следующих этапов:

1.На основе накопленных знаний составляется множество так называемых потенциальных объясняющих переменных (первичных переменных), в которое включаются все важнейшие величины, влияющие на объясняемую переменную. Такие переменные будем обозначать Х1 Х2. Хт.

2.Собирается статистическая информация о реализациях как объясняемой переменной, так и потенциальных объясняющих переменных. Формируется вектор у наблюдаемых значений переменной Y и матрица X наблюдаемых значений переменных Х1, Х2, . Хт в виде

3. Исключаются потенциальные объясняющие переменные, характеризующиеся слишком низким уровнем вариабельности.

4.Рассчитываются коэффициенты корреляции между всеми рассматриваемыми переменными.

5.Множество потенциальных объясняющих переменных редуцируется с помощью выбранной статистической процедуры

Вектор и матрица коэффициентов корреляции

Для оценивания силы линейной зависимости объясняемой переменной Y от потенциальных объясняющих переменных Х1, Х2, . Хт рассчитываются коэффициенты корреляции

Эти коэффициенты представляются в виде вектора корреляции:

Коэффициенты корреляции между потенциальными объясняющими переменными Х1, Х2, . Хт рассчитываются по формуле

образуют матрицу корреляции R:

Матрица R симметрична, т. е. rij= rji

Свойства дисперсии случайной переменной

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата её отклонения от математического ожидания: D(X)=M[X-M(X)] 2 или D(X)=M(X-a) 2 где a=M(X).

(Для дисперсии СВ Х используется также обозначение Var(X).)

Дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений СВ относительно среднего значения.

Если СВ Х – дискретная с конечным числом значений, то

.

Дисперсия D(X) имеет размерность квадрата СВ, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину .

Свойства дисперсии СВ:

1) D(C)=0, где C – постоянная величина;

3) D(X)=M(X 2 )-a 2 где a=M(X);

4)D(X+Y)=D(X-Y)=D(X)+D(Y), где X и Y – независимые случайные величины.

🎬 Видео

Собственные векторы и собственные числа линейного оператораСкачать

Ковариационная матрицаСкачать

Матрица корреляцийСкачать

Линейная зависимость и линейная независимость векторов.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

7. MathCad. Векторы и матрицыСкачать

Занятие 12. Векторы и матрицыСкачать

А.7.35 Собственные вектора и собственные значения матрицыСкачать

Теория вероятностей #25: Ковариация и корреляция / ковариационная матрицаСкачать

part7 собственные вектора матрицы ковариацииСкачать

Расчет коэффициента корреляции в ExcelСкачать

Линал 2.6. Умножение матрицы на векторСкачать

Линейная зависимость векторовСкачать

Линейная алгебра. Векторы и операции над векторами.Скачать