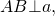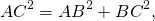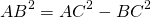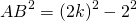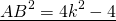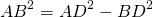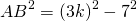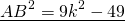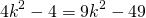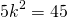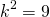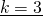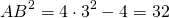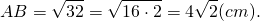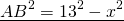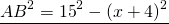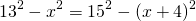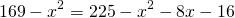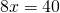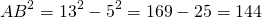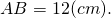Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.
Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.
Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.
Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.
Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.
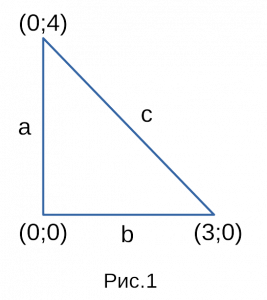
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
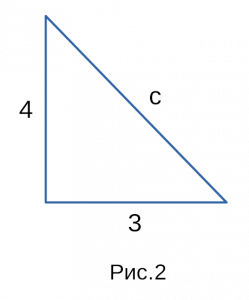
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.
Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:
Подставляем наши координаты:
В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.
Видео:Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Все формулы для треугольника
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
Видео:Как найти расстояние от вершины треугольника до ортоцентра? Профиматика и ЕГЭматика знают ответ!Скачать

2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
Видео:Как начертить Эпюр 1 КНИТУ(КХТИ) 1 курс.Найти расстояние от точки D до плоскости треугольника ABCСкачать

3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
Видео:✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать
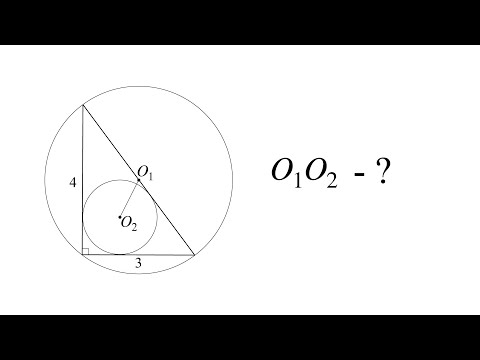
Расстояние от точки до прямой
Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.
Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.
№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

BC и BD — их проекции, BC=2 см, BD=7 см
1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим k:
5) Зная k, найдем AB:
№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

AC и AD — наклонные, AC=13 см, AD=15 см,
BC и BD — их проекции, BD-BC=4 см
1) Пусть BC=x см, тогда BD=x+4 см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим x:
5) Зная x, найдем AB:
№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.
📸 Видео
Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать
Определение расстояния от точки до плоскости треугольникаНатуральная величина расстоянияСкачать
Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Расстояние от точки до плоскостиСкачать
Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Определить расстояние от точки до плоскости (от точки D до плоскости треугольника ABC)Скачать
Построение параллельной плоскости на расстояние 30 мм.Скачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

расстояние от точки до плоскостиСкачать