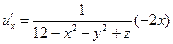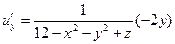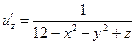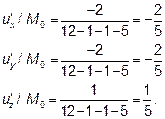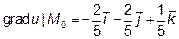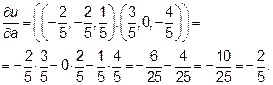Вектор grad в точке

Решение находим с помощью калькулятора.
Градиент grad u

grad u в точке А

Вектор а(2;-1;0)
Направляющие углы

Модуль вектора |a| .

Производная в точке А по направлению вектора а .

Пример №2 . Найти grad u в точке М(0,0,0), если u=х*sin(z)-y*cos(z) .
Найти производную функции u=х*y 2 +z 3 -x*y*z в точке М(1,1,2) в направлении, образующем с осями координат углы соответственно в 60 о , 45 о , 60 о .

Пример №3 . Даны функция z = f(x,y) , точка A и вектор a . Найти: 1) наибольшую скорость возрастания функции в точке A ; 2) скорость изменения функции в точке A по направлению вектора a.
z = ln(x 2 + 3y 2 ), A(1,1), a(3,2).
Примечание: наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Скачать решение

Задача 1. Найти проекции grad z в точке М(1,2) , где z=ln(4x 2 -y).

Задача 2. Найти производную функции z=х 3 -3x 2 y +3xy 2 +1 в точке М(3,1) в направлении, идущем от этой точки к точке N(6,5) .

Задача 3. Даны функция z = f(x,y) , точка A(x₀,y₀) и вектор a(a₁,a₂). Найти:
1) grad z в точке A ;
2) производную в точке A по направлению вектора a .
Решение.
z = ln(5x 2 +3y 2 ), A(1;1), a(3;2)
Скачать решение

Градиент функции онлайн

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , — частные производные функции по переменным , , соответственно.

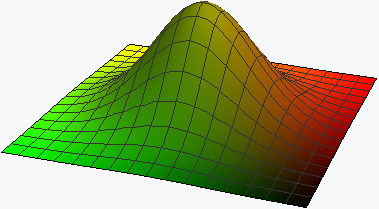
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

ЗАДАНИЕ №22

Следующая задача посвящена нахождению вектора – градиента для функции нескольких переменных.

Подробнее об этом можно прочесть в [4] гл.8 и [1]гл.XXVIII

вектор-градиент обозначается grad u или Ñu.

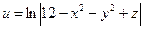
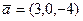
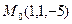
Пример 1.Даны функция трех переменных , вектор и точка .

Найти: 1) Grad u в точке M₀;

2) производную в точке M₀ по направлению вектора ;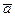

3) наибольшую крутизну поверхности u в точке M₀.

Решение:

1) Вектором градиентом функции трех переменных u(x,y,z) является вектор
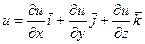
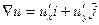
grad (или в случае двух переменных)

Найдем частные произведения функции u:

Из определения градиента следует, что эти частные производные являются проекциями вектора-градиента на оси координат. Вычислим значения частных производных в точке M_o.

Следовательно вектор-градиент в точке M₀ имеет вид:

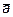
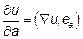
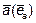
2) Производная по направлению вектора вычисляется по формуле , то есть равна скалярному произведению вектора градиента на единичный вектор, совпадающий по направлению с вектором .

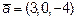
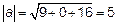
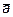
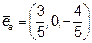
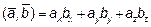
Так как , то его длина и, следовательно, единичный вектор, совпадающий по направлению с , , используя формулу скалярного произведения в координатной форме , получим

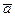
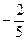
Итак производная функции u по направлению вектора равна .

3) Поскольку |grad u| есть наибольшее значение производной 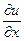в данной точке P, а направление grad u совпадает с направлением луча, выходящего из точки P, вдоль которого функция меняется быстрее всего, то направление градиента есть направление наискорейшего возрастания функции u(x,y,z)

|grad u| = .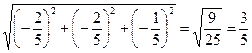

Решите самостоятельно следующие задачи:

22.1 Найти вектор-градиент функции 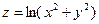в точке (1,1)

22.2 Найти производную функции 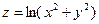в направлении вектора-градиента

Аналогичные задачи можно найти в [3] гл.8