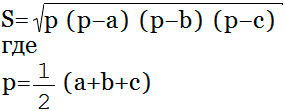Как периметр треугольника герона (5 видео)

Периметр треугольника формула герона

Содержание

Как найти периметр треугольника
Определение
Как узнать периметр треугольника
Скачать онлайн таблицу
Формула Герона для треугольника
Формула площади
Примеры задач
Формула Герона для нахождения площади треугольника
Формула Герона для треугольника
Формула площади
Примеры задач
Площадь треугольника по формуле Герона
🎥 Видео

Видео:8 класс, 18 урок, Формула ГеронаСкачать

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:найти площадь треугольника. Формула Герона. Известны 3 стороны.Скачать

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Видео:Запомни: все формулы для площади треугольникаСкачать

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Видео:Геометрия 8 класс (Урок№13 - Формула Герона.)Скачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Видео:Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

Формула Герона для треугольника

В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Формула площади

Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).

Полупериметр ( p ) вычисляется таким образом:

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Примеры задач

Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.

Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .

Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.

Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .

Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,

Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.

Остается только использовать формулу для нахождения площади:
= = .

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формула Герона для нахождения площади треугольника

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим еще один способ вычисления площади треугольника – с помощью формулы Герона. Она позволяет вычислить площадь треугольника, зная лишь его стороны, что может очень пригодиться, особенно в практических вычислениях. Мы выпишем и докажем формулу Герона, а также решим несколько задач на применение этой формулы.

Видео:Формула Герона #математика #репетиторСкачать

Формула Герона для треугольника

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Формула площади

Полупериметр ( p ) вычисляется таким образом:

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Видео:Формула ГеронаСкачать

Примеры задач

Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.

Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .

Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .

Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,

Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.

Остается только использовать формулу для нахождения площади:
= = .

Видео:Формулы равностороннего треугольника #shortsСкачать

Площадь треугольника по формуле Герона

Герон Александрийский (др.-греч. Ἥρων ὁ Ἀλεξανδρεύς)
) — греческий математик и механик. Герона относят к величайшим инженерам за всю историю человечества. Он первым изобрёл автоматические двери, автоматический театр кукол, автомат для продаж, скорострельный самозаряжающийся арбалет, паровую турбину, автоматические декорации,

прибор для измерения протяжённости дорог (древний одометр) и др. Первым начал создавать программируемые устройства (вал со штырьками с намотанной на него верёвкой).

Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки — его сторонами.

Формула Герона: