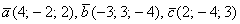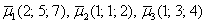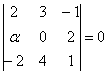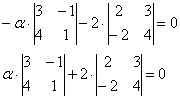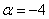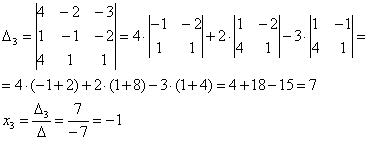Дан параллелепипед найти координаты вектора середина в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

Матрицу Х ищем по формуле:

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Координаты вектора в данном базисе.

Дата добавления: 2015-08-06 ; просмотров: 9270 ; Нарушение авторских прав

Базисом векторного пространства называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства можно представить в виде линейной комбинации векторов этой системы.

В трехмерном векторном пространстве базис состоит из трех векторов, который обычно обозначается так: <е₁, е₂, е₃ >.

Базис называется ортонормированным, если длины всех базисных векторов равны единицы, и базисные векторы попарно перпендикулярны. Ортонормированный базис обычно обозначается так: <i, j, k>.

Координатами вектора m в базисе <е₁, е₂, е₃ >называются коэффициенты разложения вектора m по векторам базиса, т.е. если m = хе₁ + уе₂ + zе₃, то числа х, у, z — координаты вектора m. В этом случае будем записывать m(х, у, z).

Имеет место теорема о координатах линейной комбинации:

1.24. Даны векторы а(2, 3, -1), b (0,1,4), с(1,0,-3). Найти координаты векторов: а) 2а — b —2с,б)а — b —3с,в)а +2b +3с),г) а — b – с,

д) 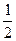( а + b), е) (а — 2 b + с).

ОТВЕТ. а) (2,5,0), б) (-1,2,4), в) (5,5,-2), г) (1,2,-2), д) (1,1,3), е) (1, ,-4)

ПРИМЕР 1.7

Даны векторы а(1,1,2), b (-2, 3 5), с(-4,1,1), d (0, -1, 3) Можно ли вектор dпредставить в виде линейной комбинации векторов а, b, с? Если да, то найти коэффициенты этой линейной комбинации.

Выясним, существуют ли такие числи х, у, z, что

d =ха +уb +z с.(1)

По теореме о координатах линейной комбинации векторов из равенства (1) получаем выражение для первой координаты вектора dчерез первые координаты векторов а, b, с, и аналогичные выражения для вторых и третьих координат

0 = х — 2у — 4 z (2)

Выясним, имеет ли эта система решение. Из (2) следует, что

Затем, подставляя (5) в (3) и (4), получаем:

Система, состоящая из уравнений (2), (3), (4), равносильна системе, состоящей из уравнений (5), (6), (7) . Ясно, что последняя система не имеет решений, следовательно, и данная система не имеет решений,. Поэтому вектор dнельзяпредставить в виде линейной комбинации векторов а, b, с. ■

1.25. Определить, какие из данных троек векторов линейно зависимы:

а) а(-3,0, 2), b (2, 1, -4), с(11, -2, -2); б) а(1, 0, 7), b (-1, 2, 4), с(3, 2, 1);

в) а(5, -1,4),b (3,-5, 2), с(-1,-13, -2).

ОТВЕТ.. а), с) линейно зависимы.

1.26. Представить вектор d как линейную комбинацию векторов а, b, с:

1)а(2,3,1), b (5, 7, 0), с(3, -2, 4), d (4, 12, -3);

2) а(5, -2, 0), b (0, -3, 4), с(-6, 0, 1), d (25, -22, 16);

3)а(3, 5, 6), b (2, -7, 1), с(12, 0, 6), d (0, 20, 18).

ОТВЕТ. 1) d = а + b + с, 2) d = 5а + 4b, 3) d = 4а – с.

1.27. Можно ли вектор d (1,1,1) представить в виде линейной комбинации векторов а(1,-1,0), b (2,2,1), с(0,-4,-1)?

ОТВЕТ.. Нет.

1.28. Даны векторы а(х, 3, 4), b (-1, 5, у).Существуют ли такие числа х и у, для которых система векторов <а, b >линейно зависима ?

ОТВЕТ. Да, х = — , у = .

ПРИМЕР 1.8

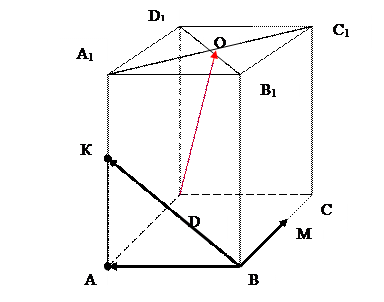
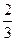
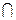
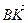
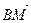
В параллелепипеде АВСDА₁В₁С₁D₁ К – середина ребра АА₁, точка М лежит на ребре ВС и ВМ = ВС, О = А₁С₁ В₁D₁. Найти координаты вектора в базисе < , , > .

Так как координаты вектора в данном базисе это коэффициенты разложения этого вектора по векторам базиса, то данную задачу можно сформулировать так: выразить вектор через векторы , , ,поэтому будем действовать так же, как при решении ПРИМЕРА 1.3.

1) = + = + = 2 + , т.е.

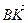
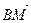
=2 + . (1).

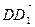
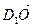
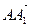
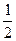
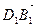
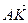
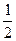
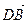
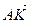
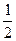
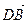
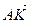
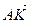
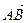
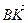
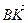
2) Выразим вектор через базисные векторы.

= + = — + .(2)

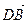
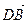
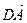
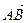
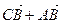
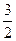
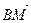
3) Выразим вектор через базисные векторы.

= + = = — – (3)

4) Подставим (2) и (3) в (1), получим

= 2(— + ) + (- – ) = 2– – .

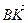
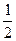
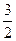
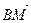
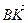
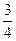
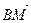
Следовательно, первая координата вектора равна 2, вторая координата равна — , третья координата равна — , т.е. (2, — , — ).

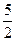
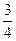
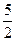
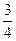
ОТВЕТ. (2, — , — ).

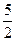
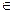
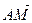
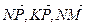
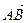
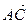
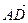
1.29. АВСD – тетраэдр. М и К – точки пересечения медиан граней ВСD и АDС, N – середина АВ, Р ВС и ВР : РС = 1 :2. Найти координаты векторов , в базисе < , , > .

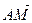
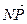
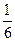
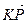
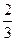
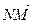
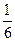
ОТВЕТ. ( , , ), ( , , 0), ( ,0, — ), (- , , ).

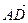
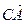
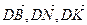
1.30. АВСD – тетраэдр. N и К середины ребер ВС и АС. Найти координаты векторов и в базисе < > .

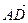
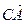
ОТВЕТ. (-1,2,-2), (2,-4,2).

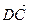
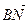
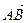
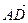
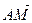
1.31. В тетраэдре АВСD М- середина ВС, а N – точка пересечения медиан грани АDС. Найти координаты векторов и в базисе < , , >.

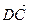
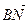
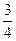
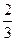
ОТВЕТ. (-1,-1,2), (- , , ).

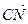
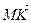
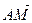
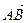
1.32. В тетраэдре АВСD N — середина ВС, а М и К – точки пересечения медиан граней ВСD и АВD. Найти координаты векторов и в базисе < , , >.

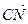
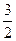
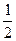
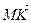
ОТВЕТ. (- , 1, ), (-1, , ).

Видео:Координаты точки и координаты вектора 1.Скачать

1.8.4. Базис и система координат пространства

Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.

Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.

И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы 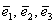, они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов!

Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)

Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не создают.

Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).

Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.

Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (почему?).

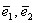
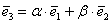
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга.

И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.

Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в этом базисе. Также говорят, что вектор представлен в виде линейной комбинации базисных векторов.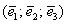

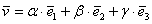
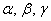
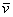
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно независимых векторов:

Выбранное (где угодно) начало координат , и некомпланарные векторы , взятые в определённом порядке, задают аффинную систему координаттрёхмерного пространства:

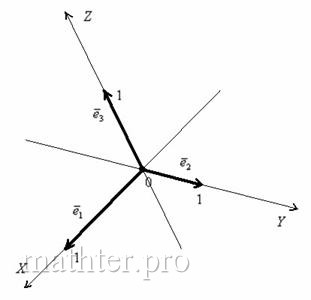
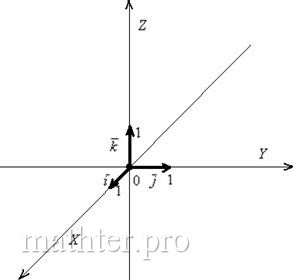
Наиболее привычным и удобным частным случаем аффинной системы координаявляется «школьная» система. Начало координат и ортонормированный базис задают декартову прямоугольную систему координат пространства:

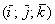
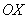
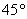
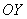
Ось абсцисс изображают под углом в по отношению к другим осям (к оси ординат и оси аппликат ). Популярный «тетрадный» масштаб: 1 ед. = 2 клетки по осям и 1 ед. = диагональ одной клетки – по оси .

И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию:

Для трёх векторов пространства эквиваленты следующие утверждения:

1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.

Противоположные высказывания, думаю, понятны.

Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём орудовать бейсбольной битой линейной алгебры:

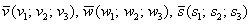
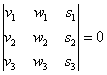
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: .

Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.

Задача 42

Проверить, образуют ли векторы базис трёхмерного пространства:

а)

б)

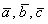
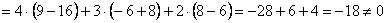
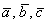
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):

, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.

Ответ: данные векторы образуют базис.

б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к книге Алгебраический Калькулятор.

Решим творческую задачку:

Задача 43

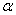
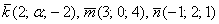
При каком значении параметра векторы будут компланарны?

Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:

По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке:

Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:

Ответ: при

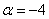
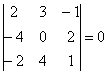
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.

И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и геометрии:

Задача 44

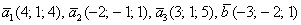
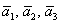
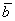
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.

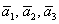
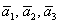
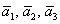
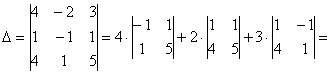
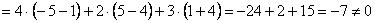
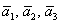
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать свой базис. И первый этап полностью совпадает с решением Задачи 42 – необходимо проверить, действительно ли векторы линейно независимы. Для этого нужно вычислить определитель, составленный из координат векторов :

, значит, векторы линейно независимы и образуют базис трехмерного пространства.

! Важно: координаты векторов 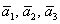обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.

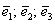
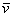
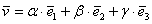
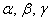
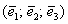
Теперь вспомним теоретическую часть: если векторы образуют базис, то любой вектор можно единственным способом разложить по данному базису: , где – координаты вектора в базисе .

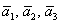
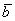
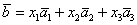
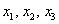
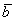
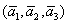
Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор можно единственным образом разложить по данному базису:
, где – координаты вектора в базисе .

И по условию требуется найти координаты .

Для удобства объяснения поменяю части местами: . В целях нахождения следует расписать данное равенство покоординатно:
– коэффициенты левой части берём из опр-ля ,
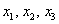
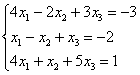
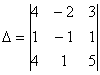
в правую часть записываем координаты вектора .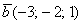

Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.

Главный определитель системы уже найден: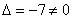
, значит, система имеет единственное решение.

Дальнейшее дело техники: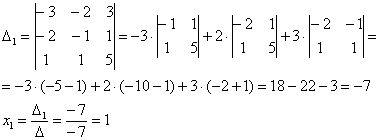


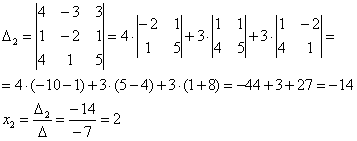
и ещё один определитель:

Таким образом:
– разложение вектора по базису .

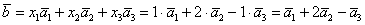
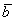
Ответ:

Такая же задача для самостоятельного решения:

Задача 45

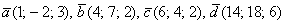
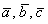
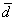
Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера.

Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.

🎦 Видео

Координаты вектора в пространстве. 11 класс.Скачать

Координаты в новом базисеСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Длина вектора через координаты. 9 класс.Скачать

Координаты вектора. 9 класс.Скачать

Правило параллелепипеда для векторовСкачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Разложение вектора по базису. 9 класс.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Математика это не ИсламСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

координаты вектора AH, который перпендикуляр из точки A к основанию параллелепипедаСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать