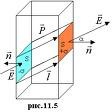
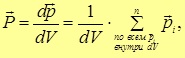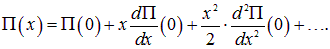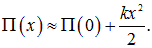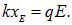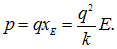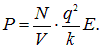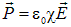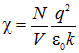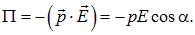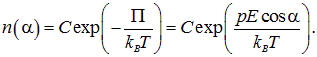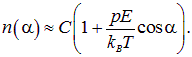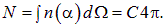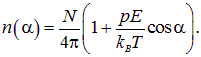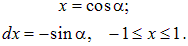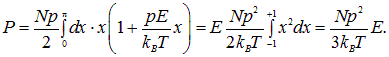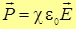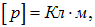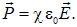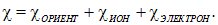ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКЕ
§1 Проводники и диэлектрики. Полярные и неполярные молекулы. Ионные кристаллы. Свободные и связанные заряды. Типы поляризации.
- Проводники и диэлектрики смотри Лекци. 1 по Электростатике.
- Типы диэлектриков.
Молекула диэлектрика, как и молекула любого другого вещества, электрически нейтральна. Это означает, что суммарный отрицательный заряд электронов равен суммарному положительному заряду ядер.

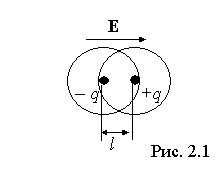
Если у молекулы в отсутствие внешнего электрического поля центры тяжести положительного и отрицательного зарядов совпадают, то есть дипольный момент молекулы 
Молекулы, у которых в отсутствие внешнего поля центры тяжести положительных и отрицательных зарядов не совпадают, то есть существует дипольный момент 
Ионные кристаллы ( NaCl , KBr , KCl ) имеют кристаллическое строение. В узлах пространственной решетки расположены с чередованием ионы разных знаков. В ионных кристаллах нельзя выделить отдельные молекулы. Их нужно рассматривать как систему двух подрешеток – положительной и отрицательной.
Кристаллическая решетка поваренной соли
ПОЛЯРИЗАЦИЕЙ диэлектрика называется процесс ориентации диполей или появление под воздействием электрического поля ориентированных по полю диполей.
(Возникновение дипольного момента в диэлектрике называется ПОЛЯРИЗАЦИЕЙ)
В результате поляризации молекула приобретает дипольный момент 
где α – поляризуемость молекулы (характеризует «реакцию» молекулы на электрическое поле). Α – характеристика атома или иона.
В качестве величины, характеризующей степень поляризации диэлектрика, принимается вектор ПОЛЯРИЗОВАННОСТИ 
где 

Трём типам диэлектриков соответствуют три типа поляризации
ЭЛЕКТРОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в неполярных молекулах. Электронная поляризация обусловлена смещением электронной оболочки атома относительно ядра во внешнем поле.
ИОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в ионных кристаллах, вызванное смещением подрешеток положительных ионов вдоль поля, а отрицательных – против поля.
- ОРИЕНТАЦИОННАЯ (ДИПОЛЬНАЯ) ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в диэлектрике с полярными молекулами вследствие ориентации дипольных моментов молекул по направлению поля.
- СВОБОДНЫЕ И СВЯЗАННЫЕ ЗАРЯДЫ
Заряды, которые при приложении внешнего электрического поля могут свободно перемещаться по проводнику, и не связаны с ионами кристаллической решетки, называются свободными.
Заряды, входящие в состав молекулы, которые под действием внешнего поля лишь немного смещаются из своих положений равновесия, и покинуть пределы молекулы не могут, называются связанными.
§2 Напряженность поля в диэлектрике.
У изотропных диэлектриков вектор поляризации линейно зависит от напряженности поля
где χ – ДИЭЛЕКТРИЧЕСКАЯ ВОСПРИМЧИВОСТЬ вещества, показывает, как диэлектрик реагирует (воспринимает) на внешнее электрическое поле.
α – характреистика отдельной молекулы (иона), χ – характеристика всего диэлектрика, то есть характреистика вещества в целом. χ не зависит от 


где 
Вне диэлектрика 


Вне диэлектрика 
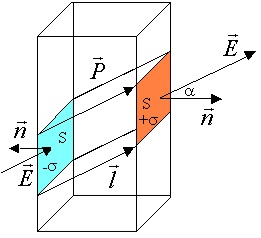
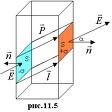
Определим поверхностную плотность связанных зарядов 
где S – площадь грани пластинки, d – её толщина. С другой стороны, полный дипольный момент равен
где Q ’ – связанный заряд каждой грани, d — плечо диполя.


или
Поверхностная плотность связанных зарядов 
Тогда поле внутри диэлектрика
Безразмерная величина 
§3 Электрическое смещение.
Теорема Гаусса для электростатического поля в диэлектрике.
Для описания электрического поля, в частности, в диэлектрике, вводят в рассмотрение вектор электрического смещения (вектор электростатической индукции) 


Результирующее поле в диэлектрике описывается вектором напряженности 



Силовые линии вектора 


ПОТОК ВЕКТОРА 
ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ:
Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов:
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

3.3. Поляризация диэлектриков
Любое вещество, вне зависимости от его агрегатного состояния и деталей его атомно-молекулярного устройства, например, атомный, молекулярный или ионный кристалл и т. п., в конечном счете, состоит из положительно заряженных ядер и отрицательно заряженных электронов.
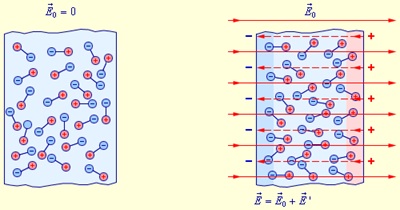
Поэтому механизм поляризации один — это смещение положительных зарядов по поляризующему полю и отрицательных зарядов против поляризующего поля (рис. 3.14). Здесь уместно подчеркнуть, что вещество поляризуется не внешним полем 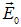
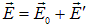
Рис. 3.14. Смещение положительных зарядов по поляризующему полю
и отрицательных зарядов против поляризующего поля
При исследовании поляризационных свойств конкретных веществ разумно и полезно выделять те главные особенности единого механизма перемещения зарядов под действием поляризующего поля, которые и определяют результат: степень и характер поляризованности вещества. Это приводит к рассмотрению целого ряда «частных» механизмов поляризации, таких как:
и многие другие.
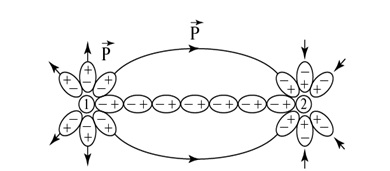
Несколько слов по поводу упомянутой выше ионной поляризации, которая имеет место в кристаллах типа поваренной соли NaCl. Под действием поля положительно заряженные ионы натрия Na + и отрицательно заряженные ионы хлора Cl – смещаются в разные стороны из своих равновесных положений, из-за чего каждая элементарная ячейка кристалла приобретает электрический дипольный момент. Этот пример полезен в следующем смысле: как бы сложно ни был устроен диэлектрик — в данном случае ионный кристалл — его поляризация обусловлена смещением в противоположные стороны положительных и отрицательных зарядов. Вопрос в том, какие конкретно носители заряда способны к такому перемещению: свободные электроны в металле, сильно связанные с ядрами электроны электронной оболочки нейтральных атомов или молекул в газе или жидкости, ионы в узлах кристаллической решетки и так далее. Определяется это тем, как устроен диэлектрик.
Процессы, происходящие в диэлектрике при его поляризации, можно понять, исходя из представлений о диэлектрике как о среде, состоящей из попарно связанных разноименных зарядов. В отличие от проводников в диэлектриках нет свободных зарядов, которые под действием внешнего поля могут двигаться по всему объему образца. Заряды, входящие в состав молекул диэлектрика, прочно связаны между собой и способны перемещаться только в пределах своей молекулы (или атома), то есть на расстоянии порядка 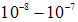
Практически во всех тех случаях, когда диэлектрик состоит из электрически нейтральных частиц (атомов и молекул), независимо от его агрегатного состояния, возможно сведение всех «подмеханизмов» поляризации к двум видам. Для этого принято делить все атомы и молекулы и состоящие из них диэлектрики на два класса:

Рис. 3.15. Поляризация неполярного диэлектрика
Рис. 3.16. Ориентационный механизм поляризации полярного диэлектрика
Здесь 
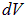
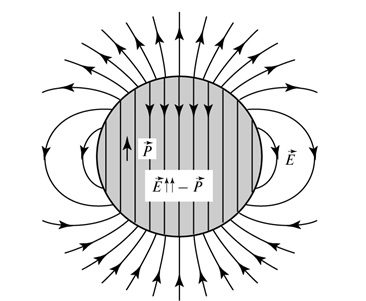
Рис. 3.17. Поляризованность и электрическое поле однородно поляризованного шара
При поляризации неполярного диэлектрика электронная оболочка атома или молекулы деформируется — электроны смещаются против поляризующего поля, ядра смещаются по полю. Возникает некоторое расстояние между ранее (в отсутствие поляризующего поля) совпадавшими центрами положительных и отрицательных зарядов. В результате атом или молекула приобретают некоторый наведенный дипольный момент.
Более или менее очевидно, что наведенный дипольный момент будет пропорционален величине внешнего электрического поля. Понять это можно, рассматривая поведение потенциальной энергии П(x) взаимодействия двух частиц, где х — расстояние между ними. Пусть равновесному состоянию соответствует расстояние 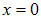
Учитывая, что первая производная в точке равновесия 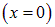
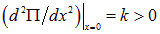
Соответственно, при отклонении от этого положения возникает сила

подобная силе упругости при растяжении пружины. Если заряды в молекуле «соединены» такой «пружиной», то при наложении поля Е новое равновесное расстояние между частицами будет определяться соотношением
В результате находим величину возникшего под действием поля дипольного момента
Умножая наведенный дипольный момент на концентрацию поляризованных молекул N/V (N — их полное число в объеме V), получаем поляризованность диэлектрика
Если записать поляризованность (3.16) в виде
где константа (для данного вещества) 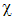
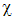
У молекул, называемых полярными, центры положительных и отрицательных зарядов сдвинуты друг относительно друга, поэтому такая молекула имеет собственный дипольный момент. При помещении такой молекулы в электрическое поле её электронная оболочка деформируется, расстояние между центрами зарядов увеличивается и к исходному собственному дипольному моменту добавляется некоторый наведенный дипольный момент. Однако, можно показать, что этот дополнительный наведенный дипольный момент много меньше собственного. Разумеется, это справедливо, если поляризующее поле много меньше поля, существующего внутри молекулы. По порядку величины внутримолекулярное поле равно атомной единице напряженности электрического поля: 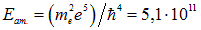
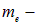
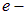
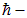

Векторы собственных дипольных моментов отдельных молекул в обычном состоянии из-за теплового движения ориентированы хаотически. Поэтому при отсутствии внешнего электрического поля средний суммарный дипольный момент любого физически бесконечно малого объема диэлектрика равен нулю. Другими словами, диэлектрик не поляризован: его поляризованность 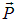
Внешнее электрическое поле стремится ориентировать дипольные моменты молекул параллельно вектору 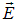
Рис. 3.18. Ориентационная поляризация диэлектрика
В соответствии с формулой (3.8) потенциальная энергия диполя во внешнем поле Е зависит от ориентации диполя
Согласно статистическому закону Больцмана (рис 3.19), описывающему распределение частиц по энергиям во внешнем поле в условиях термодинамического равновесия, число 

Здесь С — нормировочная постоянная, значение которой мы найдем позже, Т — абсолютная температура, постоянная Больцмана — kB = 1,38·10 –23 Дж/К. Вследствие малости дипольного момента молекул, для обычных (не слишком низких) температур показатель экспоненты мал, и мы можем разложить экспоненту в ряд Тейлора, оставляя первые два члена
Рис. 3.19. Л. Больцман (1844–1906) — австрийский физик
Подчеркнем, что использование приближенного выражения (3.18) и всех выводов, следующих из него, оправдано при не слишком низких температурах, когда 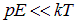
Интеграл 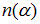
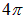
Теперь мы знаем постоянную С и можем записать выражение (3.18) в виде
Необходимо определить значение проекции суммарного дипольного момента на направление поля (другие проекции заведомо равны нулю ввиду осевой симметрии задачи). Проекция дипольного момента одной молекулы равна рcosa, следовательно полный дипольный момент Р всех молекул в единице объема равен
Интеграл по 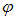
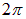
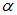
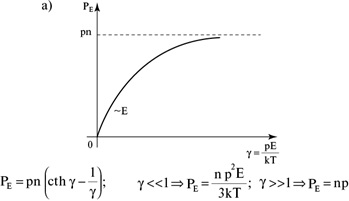
Из (3.21) вытекает, что и в случае дипольной ориентационной поляризации вещества поляризованность пропорциональна напряженности электрического поля. Более того, мы нашли зависимость поляризованности от температуры. Это закон Кюри, который подтверждается на опыте (рис. 3.20).
Рис. 3.20. Зависимость поляризованности полярного диэлектрика от температуры (точное решение)
Подводя итоги данного раздела, мы вкратце повторим основные выводы. Внешнее электрическое поле либо создает дипольные моменты, ориентированные по полю, либо ориентирует дипольные моменты отдельных молекул, и диэлектрик приобретает определенный макроскопический дипольный момент. Вектор 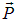
где 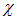
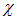
то вектор поляризации в СИ измеряется в Кл/м 2 . Его размерность совпадает с размерностью поверхностной плотности зарядов. Это наводит на мысль, что вектор поляризованности связан с плотностью поляризационных зарядов, возникающих на поверхности и в объеме диэлектрика, помещенного во внешнее поле (рис. 3.21).
Рис. 3.21. Вектор поляризованности и плотность поляризационных зарядов
Пропорциональность между поляризованностью Р и напряженностью Е внешнего электростатического поля объясняется в случае электронной и ионной поляризации тем, что с увеличением Е растут дипольные моменты отдельных атомов pi. При дипольной поляризации пропорционально увеличению напряженности внешнего электростатического поля увеличивается степень ориентации векторов p i. Выше мы нашли общие формулы для диэлектрической восприимчивости при различных видах поляризации. Следует подчеркнуть, что они справедливы для газов: мы не учитывали влияния молекул друг на друга, что допустимо для систем, где частицы не слишком плотно упакованы. Но общий вывод остается справедливым и для конденсированных сред (жидкостей и твердых тел): под действием внешнего электрического поля единица объема диэлектрика приобретает дипольный момент Р; в простейших случаях имеет место линейная зависимость
В полную диэлектрическую восприимчивость диэлектрика дают вклад все три рассмотренных механизма:
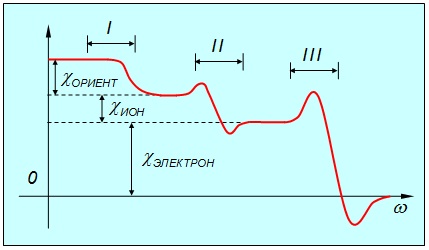
Обычно редко бывает, чтобы все доли диэлектрической восприимчивости были одинаково велики. Скажем, в ионных кристаллах дипольная часть вообще отсутствует. Экспериментально вклад каждой доли можно найти, измеряя диэлектрические проницаемости при разных частотах электромагнитной волны. При низких частотах (статическое поле, которым мы сейчас занимаемся) вклад дают все три доли диэлектрической восприимчивости (рис. 3.22).
Рис. 3.22. Зависимость полной диэлектрической восприимчивости диэлектрика 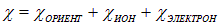
от частоты электромагнитной волны. Указаны диапазоны частот:
I — область радио- и микроволн, II — инфракрасная область, III — ультрафиолетовая область
При повышении частоты первым исчезнет вклад дипольной части: молекулы не будут успевать поворачиваться, следуя быстро изменяющемуся электрическому полю волны. Переход к новому режиму осуществляется обычно при частотах радиодиапазона. При дальнейшем росте частоты исчезнет вклад ионной части: ионы более инерционны, нежели электроны. В диапазоне оптических частот доминирует электронная доля поляризации. При переходе к еще более высоким частотам — за ультрафиолетовой областью — даже электронные облачка не будут успевать следовать за изменениями электрического поля и поляризуемость диэлектрика исчезнет.
Приведем пример: у поваренной соли NaCl диэлектрическая проницаемость в статическом поле равна 5,62, а в поле электромагнитной волны оптического диапазона — всего лишь 2,25. Дипольная поляризуемость в таких кристаллах отсутствует, и различие следует приписать ионной поляризуемости.
Дополнительная информация
Видео:Дипольный момент (видео 26) | Химические связи и структура молекул | ХимияСкачать

Вектор поляризации
Вы будете перенаправлены на Автор24
Видео:Билет №06-08 "Диэлектрики"Скачать

Что такое вектор поляризации
Для того, чтобы с количественной точки зрения описать поляризацию диэлектрика, пользуются вектором поляризации (поляризованностью ($overrightarrow
$)), который является электрическим моментом единицы объема диэлектрика:
где $overrightarrow$ — дипольный момент элемента диэлектрика.
В том случае, если диэлектрик состоит из неполярных молекул, то дипольный момент диэлектрика можно разделить на две части: момент каждой молекулы и дипольные моменты всех молекул в единице объема.
Получается, что для неполярных молекул вектор поляризованности можно определить, как:
где суммирование идет относительно всех молекул в объеме $triangle V$. $N$ — концентрация молекул, $overrightarrow
$ — индуцированный дипольный момент (Он одинаковый у всех молекул). $overrightarrow
uparrow uparrow overrightarrow$.
Видео:Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Формула поляризованности для полярных молекул
Формула поляризованности для полярных молекул имеет вид:
где $leftlangle overrightarrow
rightrangle $ — среднее значение дипольных моментов, которые равны по модулю, но разнонаправлены.
В изотропных диэлектриках средние дипольные моменты совпадают по направлению с напряженностью внешнего электрического поля. У диэлектриков с полярного типа молекулами, вклад в поляризованность от наведенных зарядов много меньше, чем вклад от переориентации поля.
Ионная решеточная поляризации описывается формулой (3). В большинстве случаев такая поляризация является анизотропной.
У электретов (диэлектрические вещества, которые в отсутствии электрического поля долгое время сохраняют поляризованность) и сегнетоэлектриков (диэлектрические вещества, которые при определенных температурах могут спонтанно поляризоваться при отсутствии внешнего электрического поля) поляризованность может быть отлична от нуля даже если $overrightarrow=0.$ У остальных диэлектриков при $overrightarrow=0$, $overrightarrow
=0$. У изотропных диэлектриков поляризованность связана с напряженностью поля в той же точке уравнением (система СИ):
[overrightarrow
=varkappa _0overrightarrow left(4right),]
где $varkappa $ — диэлектрическая восприимчивость (безразмерная величина).
В анизотропных диэлектриках направление вектора напряженности и вектора поляризации не совпадают. И их связь устанавливается в виде:
где индексы i,j — нумеруют компоненты по осям декартовой системы координат ($i=x, y,z;j=x, y,z. )$), $_$ — тензор диэлектрической восприимчивости.
Зависимость $overrightarrow
(overrightarrow)$ в общем случае представлена в виде:
Формула (6) показывает, что поляризованность зависит не только от первой степени напряженности электрического поля, но и от ее высших степеней. Если зависимость в (6) от высших степеней играет существенную роль, то диэлектрик нелинейный. Подобная нелинейность проявляется в сильных полях, так же существуют некоторые специальные вещества. Если нелинейность не существенна, то используют формулы вида (5).
При неоднородной поляризации, поляризационные заряды могут появляться не только на поверхности диэлектрика, но и в его объеме. Плотность объемных связанных зарядов ($_$) равна:
Формула (7) показывает, что объемные заряды возникают только в случае неоднородной поляризации. При переходе из одного диэлектрика в другой, поверхностная плотность связанных зарядов ($_$) равна:
где $overrightarrow$- единичный вектор нормали, который направлен из первой во вторую среду, $overrightarrow
;;overrightarrow
$ — векторы поляризации второй и первой среды. Заметим, что вакуум можно рассматривать как диэлектрик, поляризованность которого равна нулю.
Единица измерения $left[Pright]=frac$.
Готовые работы на аналогичную тему
Задание: Чему равна объемная плотность зарядов в диэлектрике, если вектор поляризованности задан функцией: $overrightarrow
=frac<overrightarrow>,$ где $overrightarrow$ — единичный орт, r — модуль радиус-вектора.
Основой для решения задачи служит формула связи плотности объёмных зарядов с вектором поляризации диэлектрика:
В нашем случае, формула (1.1) преобразуется к виду:
Ответ: Объемная плотность зарядов при заданном векторе поляризованности равна нулю.
Задание: Вектор поляризации бесконечной пластины поляризованного диэлектрика задан выражением: $overrightarrow
Вектор напряженности и вектор поляризации направлены в разные стороны.
Основанием для решения задачи выберем уравнение:
Следовательно, если мы знаем закон изменения вектора поляризации из условия задачи, следовательно:
Разность потенциалов может быть найдена, если известен закон изменения напряженности, как:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 12 2022
🎥 Видео
Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Диэлектрики в электрическом поле. 10 класс.Скачать

Электростатика | электрический дипольСкачать

Поляризация диэлектрикаСкачать

Лекция 4 -1 Поляризация диэлектриковСкачать

40. Электрический дипольСкачать

Лекция 3-1 Электрический дипольСкачать

Лекция 4-5 Доказательство теоремы Гаусса для вектора поляризацииСкачать

Диэлектрики в электростатическом поле. Поляризация диэлектриков | Физика 10 класс #48 | ИнфоурокСкачать

Как отличать полярные молекулы от неполярных? Дипольный момент.Скачать

Диэлектрик в электрическом полеСкачать

Лекция №4 "Электроемкость. Дипольный момент"Скачать

Лекция 237. Вектор электрической индукцииСкачать

Поляризация света и закон МалюсаСкачать

ЧК_МИФ 3_1_5_1 _(L4) ВЕКТОР ЭЛЕКТРИЧЕСКОЙ ПОЛЯРИЗАЦИИСкачать

ЧК_МИФ 3_1_5_1 _(L3) ВЕКТОР ЭЛЕКТРИЧЕСКОЙ ПОЛЯРИЗАЦИИСкачать





 ЭЛЕКТРОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в неполярных молекулах. Электронная поляризация обусловлена смещением электронной оболочки атома относительно ядра во внешнем поле.
ЭЛЕКТРОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в неполярных молекулах. Электронная поляризация обусловлена смещением электронной оболочки атома относительно ядра во внешнем поле.