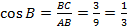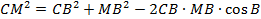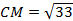Косинус вершины равнобедренного треугольника

Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.

• a² = b² + c² – 2b.c.cosα
• b² = a² + c² – 2a.c.cosβ
• c² = a² + b² – 2a.b.cosγ

Например:

Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.

Решение по формуле a² = b² + c² – 2b.c.cosα:

cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)

a² = 12² + 8² – 2×12×8×(- 1/2)

Длина третьей стороны — примерно 17,436 см.

Видео:Косинус двойного угла в равнобедренном треугольнике #егэ2024Скачать

Следствия

Следствие косинуса угла треугольника

При помощи теоремы косинусов можно найти косинус угла треугольника.

Используйте теорему косинусов, чтобы найти угол β.

Решение:

Будем использовать эту версию формулы:

cos β = (6² + 8² − 7²) / 2×6×8

Следствие верхней части формулы cos α

Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):

• b²+c²−a² 0, значит угол α — острый.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Доказательство теоремы косинусов

Нужно доказать, что c² = a² + b² − 2a.b.cos C

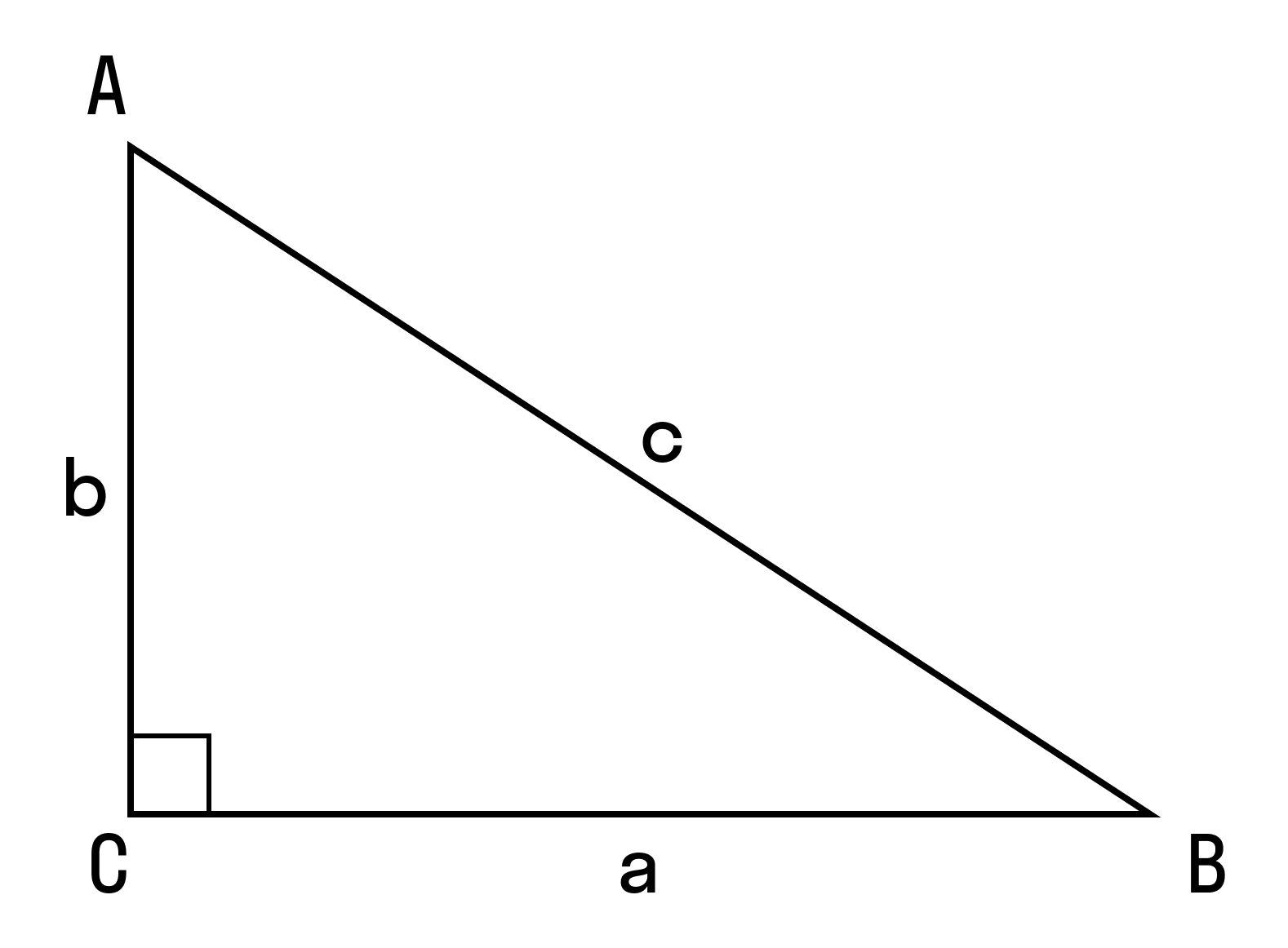
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.

2. Вычитаем это из стороны b, так мы получим DA:

3. Мы знаем из определения синуса, что в том же треугольнике BCD:

sin C = BD/a BD = a.sinC.

4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²

5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²

6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C

6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC

7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC

8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Теорема косинусов для равнобедренного треугольника

В равнобедренном треугольнике:

• две его стороны равны;
• углы при основании равны.

Используем формулу теоремы косинусов

a² = b² + c² – 2b.c.cosα

Подставляем все известные:

x² = 8² + 8² – 2×8×8×cos140º

x² = 64 + 64 – 128 × (-0,766)

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Теорема синусов

Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Теорема Косинусов Для Треугольника Формула

Видео:☀️ГЕОМЕТРИЯ В ЕГЭ | РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК | ЗАДАНИЕ 3 ЕГЭ 2022 | СИНУСЫ, КОСИНУСЫ, ТАНГЕНСЫСкачать

Теорема косинусов для треугольника формула

• Формула теоремы косинусов
• Следствие из теоремы косинусов
• Примеры решения задач

Видео:Равнобедренный треугольник и теорема косинусов. Медиана и равновеликие тр-к. Система уравнений. ЕГЭ.Скачать

Формула теоремы косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними.

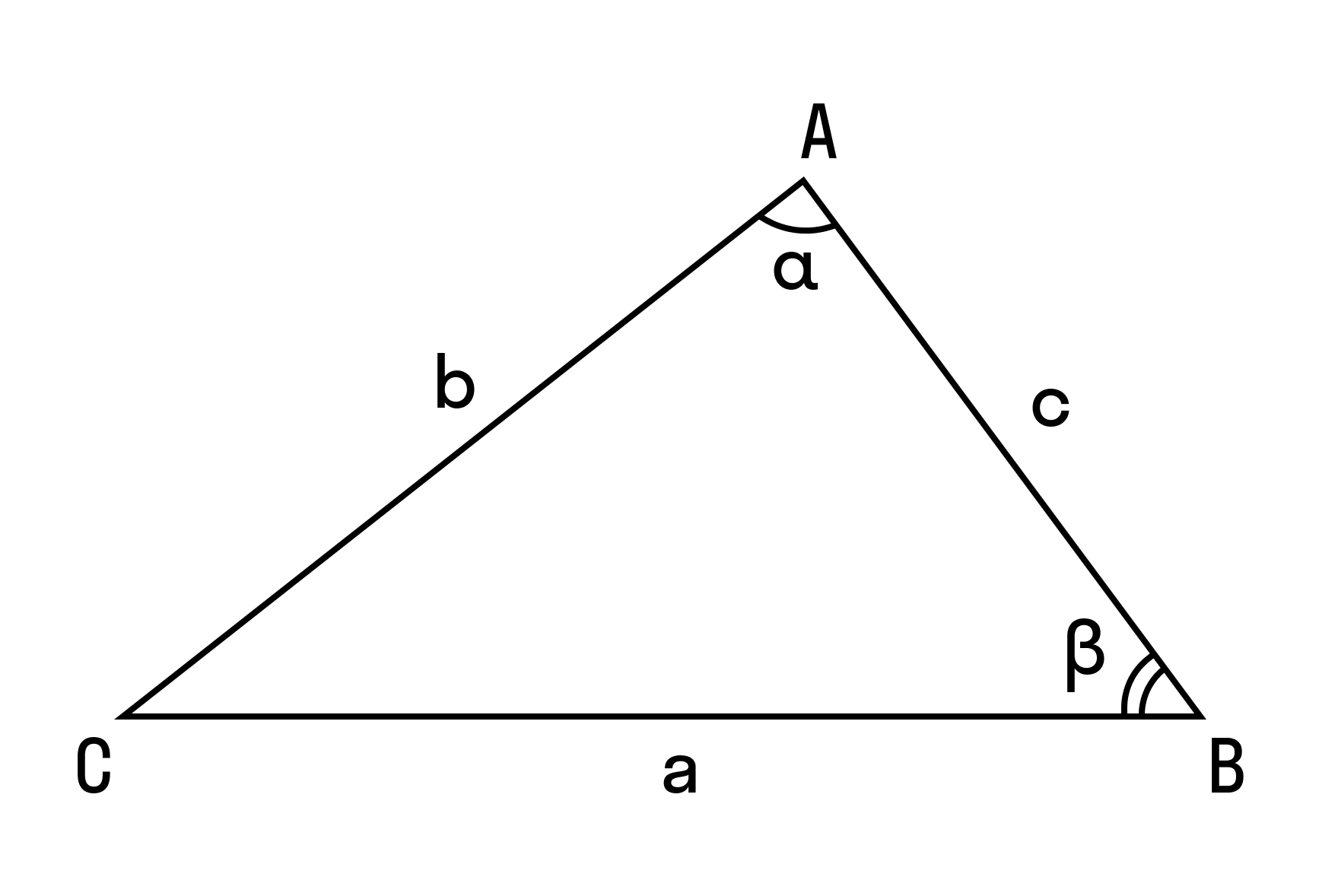
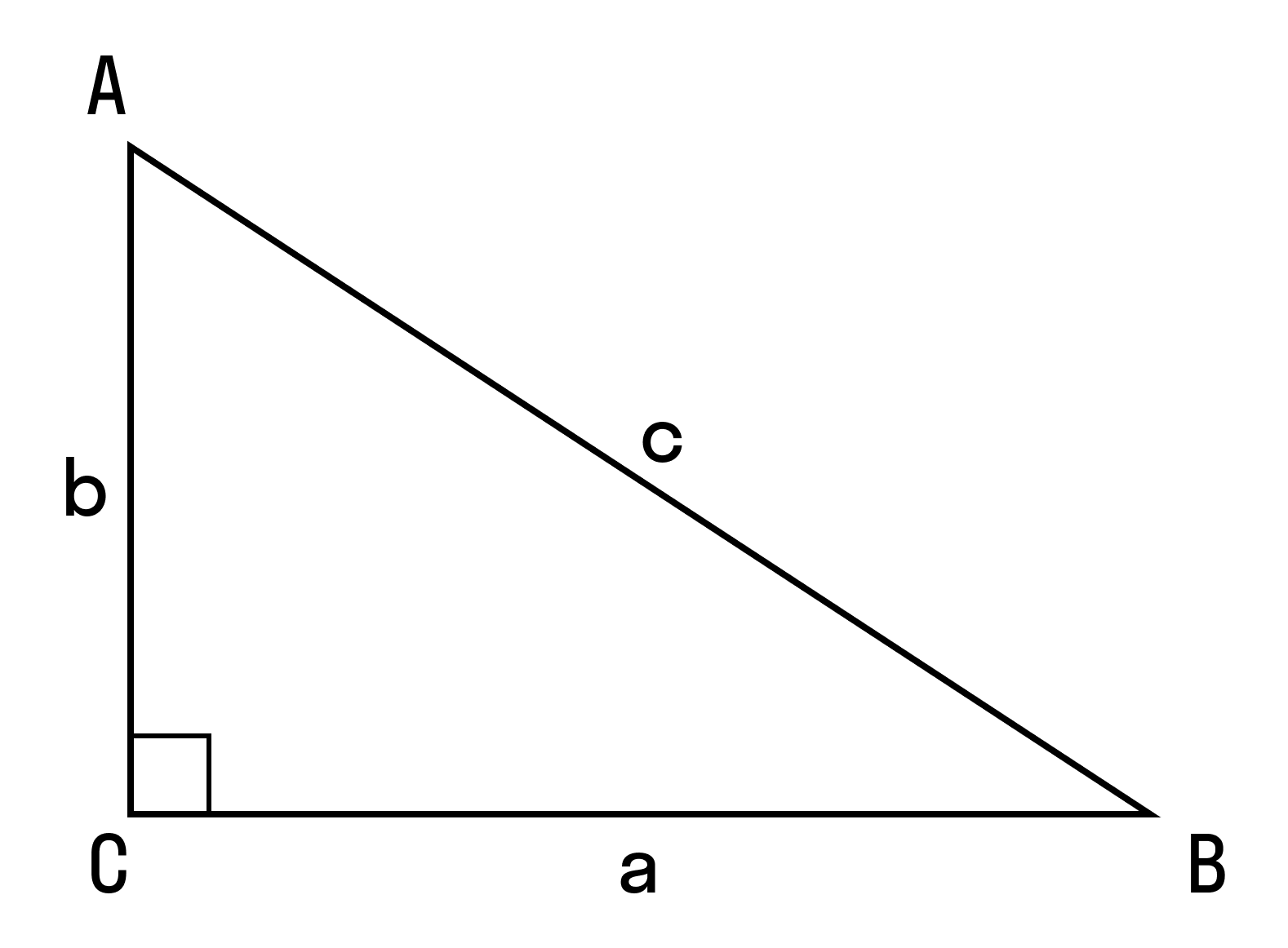
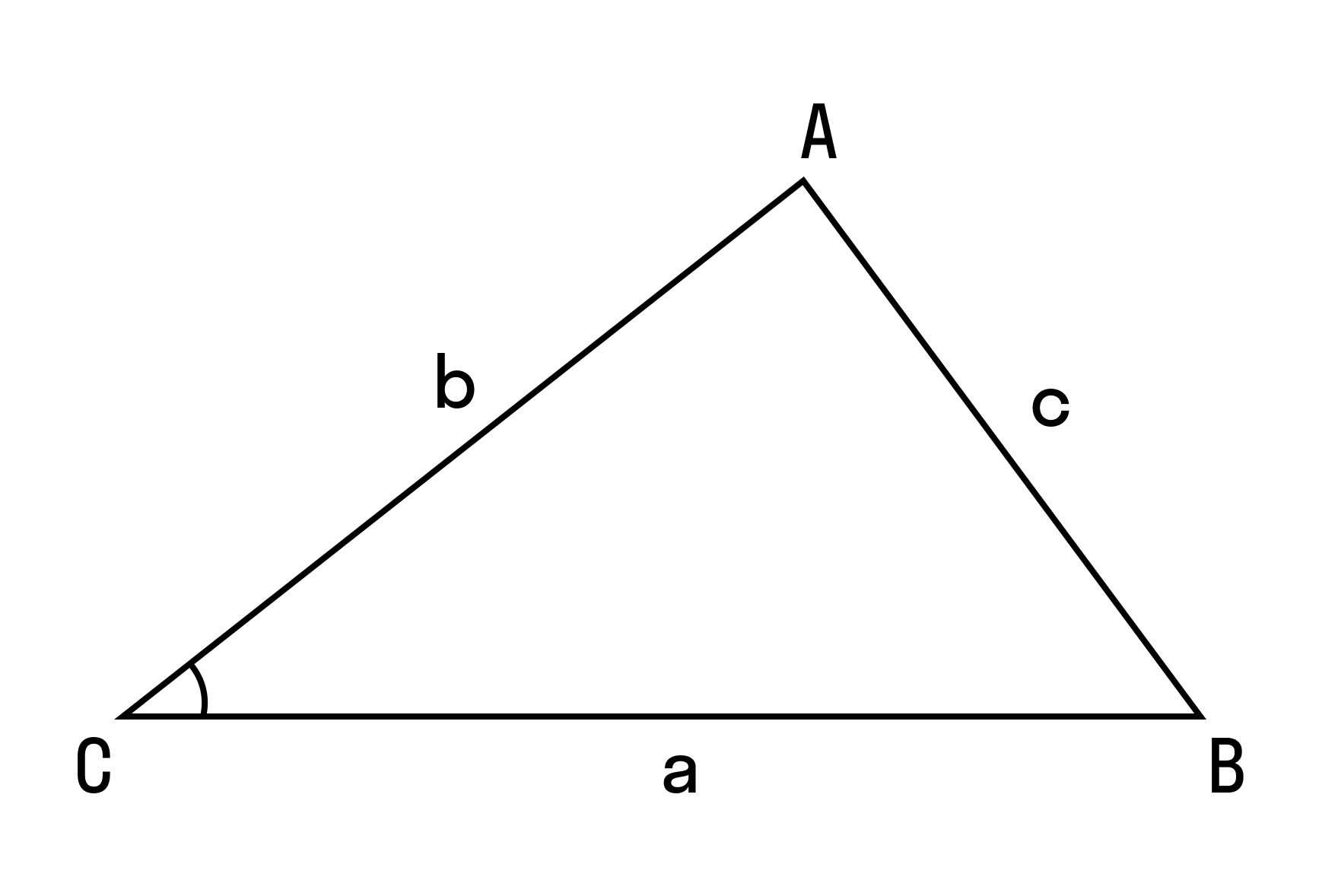
То есть для плоского треугольника (рис. 1) со сторонами $a$, $b$ и $c$ и углом $alpha$, противолежащим стороне $a$,
справедливо соотношение:

Теорема косинусов является обобщением теоремы Пифагора.
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов,
были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» древнегреческого математика Евклида
(ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков
стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог,
астроном и математик Региомонтан (1436 — 1476), назвав её «теоремой Альбатегния» (по имени выдающегося средневекового астронома и
математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 — 929).

В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её
стали записывать в принятых по сей день алгебраических обозначениях.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Следствие из теоремы косинусов

Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис. 1):

Если $b^+c^-a^>0$, то угол $alpha$ — острый;

Если $b^+c^-a^=0$, то угол $alpha$ — прямой;

Если $b^+c^-a^ lt 0$, то угол $alpha$ — тупой.

Видео:№ 6 ЕГЭ по математике профиль. Равнобедренный треугольник. Косинус ,тангенс.Скачать

Примеры решения задач

Задание. В треугольнике $ABC AC=3, BC=5$ и $AB = 6 .$ Найти угол, противолежащий стороне $AB$

Решение. Согласно следствию из теоремы косинусов, имеем:

$$angle A C B=arccos left(-fracright)$$

Ответ. $angle A C B=arccos left(-fracright)$

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Задание. Задан треугольник
$ABC$, длины сторон которого $AC=17, BC=14, angle ACB=60^$.
Найти длину третьей стороны рассматриваемого треугольника.

Решение. Согласно теореме косинусов

$$A B^=A C^+B C^-2 cdot A C cdot B C cdot cos angle A C B=$$

$$=17^+14^-2 cdot 17 cdot 14 cdot cos 60^=289+196-238=24$$

Ответ. $A B=sqrt$

Видео:ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Теорема косинусов для треугольника формула

Видео:№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

Геометрическая фигура

Прежде чем рассматривать теорему косинусов для треугольника и формулу, которая математически ее выражает, следует познакомиться с самим геометрическим объектом подробнее.

Треугольник представляет собой плоскую фигуру, которая состоит из двух типов элементов:

• трех отрезков, являющихся сторонами;
• трех вершин, образованных на пересечении отрезков и определяющих углы фигуры.

Если две стороны треугольника равны между собой и отличаются от третьей, его называют равнобедренным. Если все имеют одинаковую длину, речь идет о равностороннем объекте. Важным свойством любого треугольника является равенство суммы его трех углов 180°. Этот факт справедлив для всех типов фигуры на плоскости.

Важные линии

Для описания характеристик объекта в геометрии используют специальные линии. Основными из них являются:

• биссектриса — прямая, выходящая из произвольной вершины и делящая ее угол на 2 равные части;
• высота — перпендикуляр, который начинается на произвольной вершине и с противоположной стороной образует прямой угол;
• медиана — линия, которая делит на 2 одинаковые по площади части треугольник, пересекает противоположную сторону фигуры ровно посередине.

Для равносторонней фигуры все 3 типа линий совпадают друг с другом, для равнобедренного треугольника только для угла, образованного равными сторонами, они являются одинаковыми.

Основные законы

О треугольнике человечеству известно все, поскольку это самая простая геометрическая фигура. Кроме того, до настоящего времени дошли некоторые работы греческих мыслителей и даже древних египтян, которые были посвящены рассмотрению ее свойств. В общем случае можно назвать 3 основные теоремы, которые в полной мере описывают главные характеристики треугольника. К ним относятся:

1. Равенство площади фигуры половине произведения высоты на длину стороны, на которую она падает — ее принято называть основанием. Помимо этой формулы, существует еще одно выражение, которое позволяет получить тот же результат, но с использованием длин трех сторон и без проведения дополнительных геометрических построений.
2. Теорема синусов.
3. Закон косинусов.

Эти 3 теоремы и соответствующие им математические выражения являются независимыми и применяются для решения многих практических проблем.

Видео:ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Теорема косинусов

Она также звучит как закон косинусов для треугольника и представляет собой обобщение теоремы Пифагора на фигуру произвольного типа. Ее формулировка связывает 3 стороны и угол в единое равенство. Закон косинусов заключается в следующем: квадрат произвольной стороны треугольника равен сумме квадратов двух оставшихся его сторон за вычетом удвоенного произведения их длин, которые умножены на косинус угла между ними.

Чтобы записать соответствующее математическое выражение, следует ввести некоторые обозначения. Пусть в фигуре ABC сторона, которая лежит напротив угла C, то есть AB = c, по аналогии, BC = a и AC=b. Углы при вершинах A, B и C удобно обозначать малыми греческими буквами α, β и γ, соответственно. Тогда формула теоремы косинусов запишется в следующем математическом виде:

c = a + b — 2*a*b*cos (γ).

Зная 3 любых элемента фигуры, можно вычислить все остальные ее характеристики. При этом хотя бы одна из известных величин должна быть линейным параметром. Это утверждение доказать несложно, если представить 2 подобных треугольника, которые имеют попарно равные углы, но разную длину сторон (одна фигура является миниатюрной копией другой).

Иными словами, знание трех углов не является достаточным условием для определения свойств треугольника.

Историческая справка

Практически во всех языках мира теорема носит название закона косинусов и не имеет конкретного автора. Однако, во французском языке она носит имя персидского математика Аль-Каши, жившего в конце XIV — начале XV веков. Согласно историческому анализу, именно с теориями этого философа связана современная формулировка теоремы.

Взаимоотношением между сторонами треугольника человечество интересовалось с давних времен. В труде греческого философа Евклида, который называется «Элементы» и датируется III веком до н. э., появляется впервые некое подобие рассматриваемого закона. Однако Евклиду не были известны тригонометрические функции, поэтому в своем труде он отдельно рассматривал тупоугольные и остроугольные фигуры и приводил для их сторон соответствующие равенства через известные длины, например, высоту.

В начале X века, когда в мире правили Средние века, арабский математик и астроном Аль-Баттани использовал работы Евклида для сферической геометрии. Его достижения сделали возможным проведения некоторых космических расчетов, например, вычисление расстояния от Земли до Солнца.

Первые таблицы тригонометрических функций синуса и косинуса появились приблизительно в XV веке. Эти достижения в математике позволили Аль-Каши, математику из школы Самарканда, переформулировать закон косинусов в удобном для использования виде. Впоследствии француз Франсуа Виет независимо от Аль-Каши получил то же самое математическое выражение для сторон треугольника с использованием тригонометрических функций.

Начиная с конца XVII столетия, когда швейцарец Леонард Эйлер ввел в математику новую нотацию, теорема Аль-Каши приобрела современную форму.

Способы доказательства

Кратко следует отметить, что существуют несколько способов доказательства теоремы. Среди них можно перечислить следующие:

• через разложение площадей многоугольников;
• с использованием теоремы Пифагора, свойств высоты и формулы косинуса в треугольнике;
• применяя окружность и ее геометрические свойства;
• с помощью векторов и их скалярного произведения.

Последний способ доказательства теоремы косинусов является самым простым и носит общий характер. Его может реализовать каждый школьник, который умеет вычитать вектора друг из друга и знает, как рассчитывается их скалярное произведение.

Применение для разных видов треугольников

Закон косинусов служит для определения неизвестных длин сторон либо углов в треугольнике. Однако общая математическая формулировка имеет ряд частных случаев в зависимости от типа фигуры, к которой ее применяют.

Для равнобедренного треугольника, у которого стороны a и b равны, нахождение c сведется к вычислению следующего равенства:

В случае равностороннего треугольника все стороны равны a = b = c. Все углы также являются одинаковыми и соответствуют 60°(180°/3). Для такой фигуры нет смысла в использовании теоремы, поскольку в ней всегда существует лишь одна неизвестная — сторона a.

Прямоугольный треугольник по отношению к теореме косинусов является специальным случаем. Благодаря этой фигуре появились понятия синуса, косинуса, тангенса и котангенса как функций, отражающих взаимоотношения между катетами и гипотенузой.

Каждый школьник знает, что возведенная длина гипотенузы в квадрат эквивалентна сумме квадратов длин двух других сторон, называемых катетами. Однако, мало кто понимает, что это математическое равенство является не чем иным, как частным случаем закона косинусов. Показать это несложно, если записать изучаемую теорему для гипотенузы c. Тогда получается следующее равенство:

c = a + b — 2*a*b*cos (90 °).

Если обратится к таблице тригонометрических функций, в ней видно, что косинус прямого угла равен нулю. В результате вычитаемое в правой части равенства обращается в ноль, и равенство сводится к типичной теореме Пифагора.

Видео:Вывод синуса двойного угла через площадь равнобедренного треугольника #егэ2024Скачать

Пример решения задачи

Известно, что стороны треугольника равны 6 см, 8 см и 10 см. Необходимо найти площадь этой фигуры.

Для решения задачи можно воспользоваться ресурсами интернета, которые предлагают множество сайтов, где с использованием онлайн-калькуляторов можно по известным данным найти нужную величину. Тем не менее представляет интерес решить эту задачу с использованием теоремы косинусов.

Площадь любого треугольника может быть вычислена так:

Здесь h — высота, проведенная к a. Известные стороны a = 6 см, b = 8 см, c = 10 см. Чтобы найти высоту h следует сначала рассчитать угол между a и c. Для этого можно применить закон косинусов:

β = arccos ((a + c — b )/(2*a*c)) = arccos ((6 + 10 — 8 )/(2*6*10)) = 53,13 °.

Теперь, если рассмотреть треугольник, образованный высотой h, стороной c и частью стороны a, можно увидеть, что он является прямоугольным (c — гипотенуза). В нем h может быть найдена через синус угла β:

h = c*sin (β) = 10* sin (53,13 °) = 8 см.

Длина высоты h равна таковой для стороны b. Это означает, что исходный треугольник являлся прямоугольным (можно проверить через теорему Пифагора). Его площадь составляет:

S = ½*a*h = ½*a*b = ½*6*8 = 24 см

Таким образом, теорема косинусов является универсальным инструментом для решения геометрических задач с треугольниками. С помощью нее по трем известным параметрам можно найти все остальные характеристики фигуры, включая ее площадь.

Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Теорема косинусов и синусов

О чем эта статья:

Видео:Геометрия 8. Урок 11- Синус, Косинус, Тангенс и Котангенс угла в прямоугольном треугольнике.Скачать

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

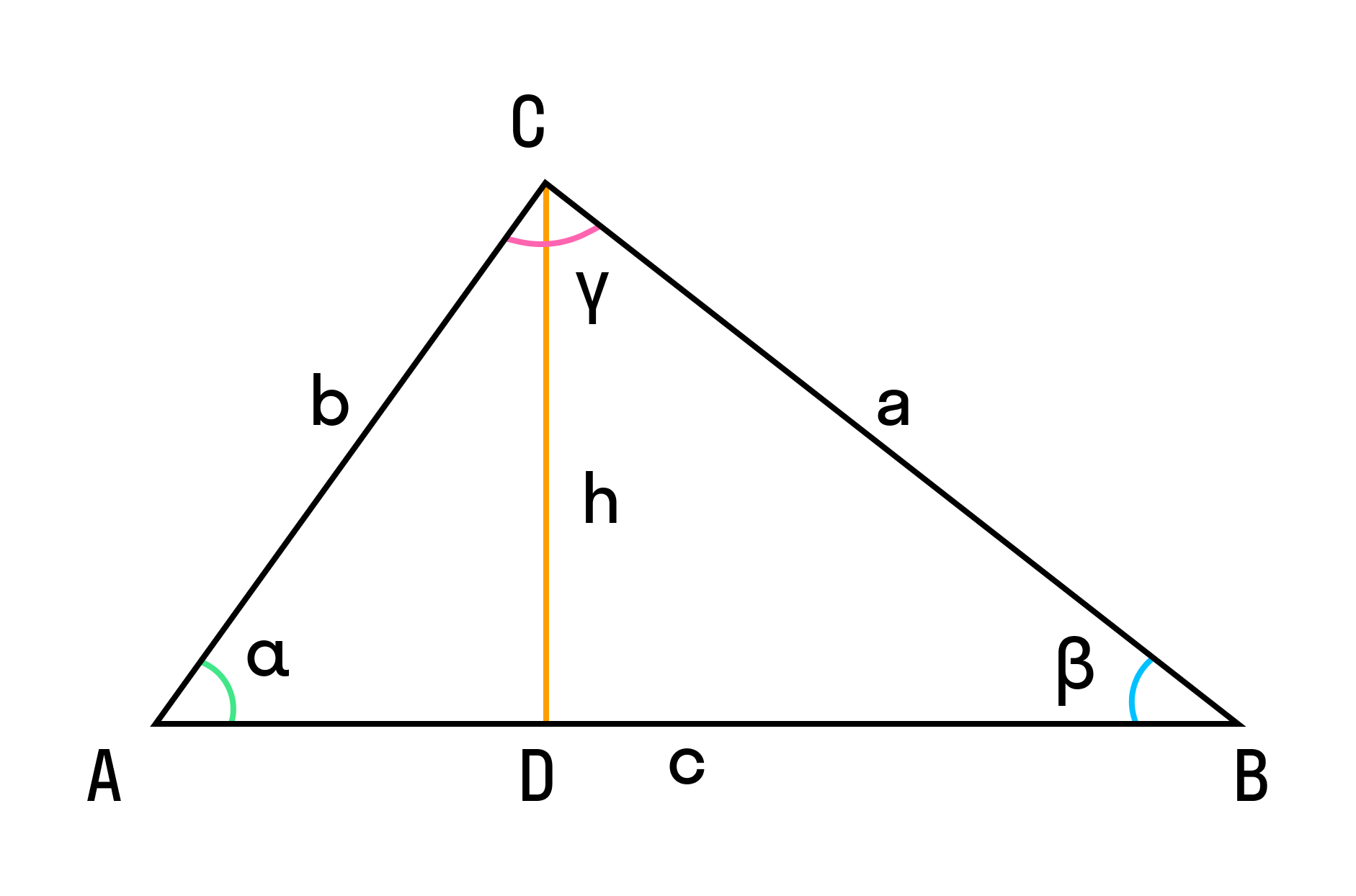
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Видео:Спидран: Как запомнить таблицу синусов и косинусов за 1 минуту? Евгений ДолжкевичСкачать

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Видео:Теорема косинусов #shortsСкачать

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Видео:КОСИНУС НА ПАЛЬЦАХ 🖐 #shorts #егэ #огэ #математика #профильныйегэСкачать

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Видео:Как запомнить значения синусов и косинусов?! #математика #синус #косинус #геометрия #егэ #shortsСкачать

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.