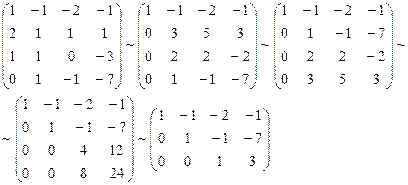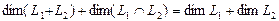Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .
Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров ;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,
– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.
Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.
Видео:Линейная оболочка. Базис и размерностьСкачать
Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .
3. Из последних строк матрицы составить матрицу .
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы составляем матрицу искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы . Искомая размерность .
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;
– из последних столбцов матрицы составить фундаментальную матрицу .
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .
2. Столбцы являются искомым базисом, так как они линейно независимы и .
Видео:Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать
Линейные оболочки и подпространства
Определение. Подпространством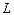 
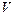
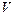
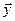
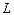
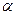
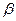
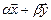
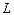
линейного пространства 
называется множество векторов из такое, что для любых двух векторов
и 
из и любых двух вещественных чисел 
и 
линейная комбинация 
также принадлежит .
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 
называется множество всех линейных комбинаций векторов . Обозначается 
.
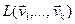
Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств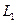 
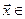
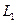
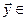
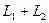
и 
называется множество всех векторов 
, представимых в виде 
, где 
, 
. Обозначается 
.
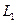
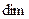
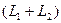
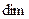
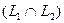
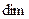
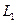
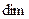
Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством
+ 
= + .
Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами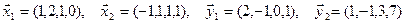 
.
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства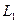 
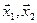
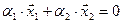
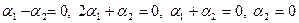
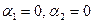
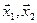
, порождённого векторами 
, равенство нулю линейной комбинации 
, эквивалентное системе уравнений 
, достигается лишь при условии 
. Следовательно, векторы линейно
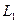
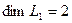
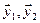
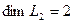
независимы и размерность подпространства равна 2: 
. Для подпространства , порождённого векторами 
, проводя аналогичный анализ, получим 
.
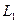
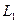
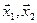
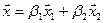
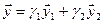
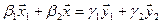
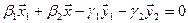
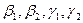
Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор 
подпространства является линейной комбинацией базисных векторов : 
. Аналогично для подпространства имеем 
, тогда условие принадлежности пересечению есть 
или 
.
Это условие представляет собой систему уравнений относительно коэффициентов 
. Составим матрицу системы и упростим её с помощью элементарных преобразований: 
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим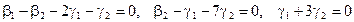 
,
откуда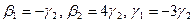 
.
Полагая свободное неизвестное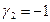 
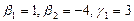
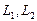
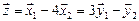
, для остальных имеем
. Итак, пересечение подпространств 
имеет один базисный вектор
.
Размерность пересечения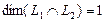 
. Следовательно, в соответствии с равенством
размерность суммы подпространств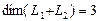 
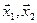
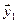
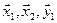
. В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором 
. В линейной независимости векторов 
убедиться нетрудно.
Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами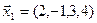 
, 
, 
, 
, 
.
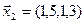
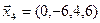
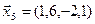
3.40. Найти размерность и какой-либо базис линейной оболочки векторов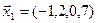 
, 
, 
, 
, 
.
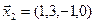
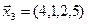
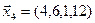
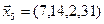
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 
последовательностей в пространстве сходящихся последовательностей;
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале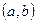 
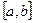
функций в пространстве функций, непрерывных на отрезке 
.
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;
б) векторов из пространства R n , координаты которых удовлетворяют уравнению 
;
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве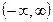 
функций в пространстве функций, ограниченных на том же множестве.
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а)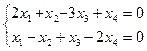 
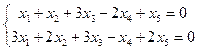
; б) 
;
в)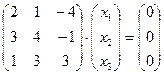 
.
3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению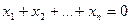 
;
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами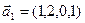 
, 
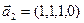
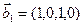
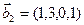
и 
, 
. Является ли эта сумма прямой суммой?
3.46. Найти размерность суммы и пересечения линейных оболочек векторов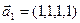 
, 
, 
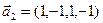
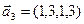
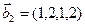
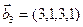
и 
, 
, 
. Является ли их cумма прямой?
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 
и 
, если
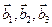
а)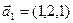 
, 
, 
, 
, 
, 
;
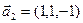
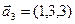
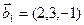
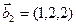
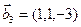
б)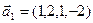 
, 
, 
, 
, 
, 
.
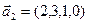
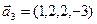
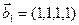
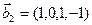
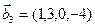
3.48. Найти базис суммы и пересечения линейных оболочек 
и 
, если
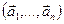
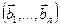
а) 
, 
, 
, 
;
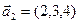
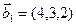
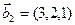
б)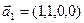 
, 
, 
, , 
, 
.
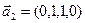
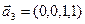
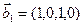
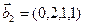
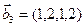
Является ли прямой сумма этих подпространств?
📺 Видео
Линал 2.2. Линейная оболочкаСкачать
Линейная зависимость и линейная независимость векторов.Скачать
Как разложить вектор по базису - bezbotvyСкачать
Высшая математика. Линейные пространства. Векторы. БазисСкачать
Связь линейных систем и линейных оболочек. ТемаСкачать
Линейные оболочки. ТемаСкачать
Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать
Базис линейного пространства (01)Скачать
Линейная зависимость векторов. РангСкачать
Анализ данных (Линейная оболочка и система)Скачать
Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать
15. Однородная система линейных уравнений / фундаментальная система решенийСкачать
Линейная комбинация векторовСкачать
Линейные оболочки. ВопросыСкачать
Линейная зависимость и линейная независимость. ТемаСкачать
Образуют ли данные векторы базисСкачать
Линейные оболочки. ОтветыСкачать
Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать
