Перпендикуляр к плоскости равностороннего треугольника

1)Верно ли, что две прямые, перепендикулярные одной плоскости, параллельны ?

2)Может ли прямая, перпендикулярная к плоскости, быть параллельна прямой, лежащей в этой плоскости?

3)OA-прямая, перпендикулярная к плоскости равностороннего треугольника АВС. Назовите отрезок, равный отрезку ОС.

4)Верно ли, что длина перпендикуляра меньше длины проекции наклонной, проведённой из этой же точки ?

5)Может ли угол между прямой и плоскостью быть тупым?

6)SA-перпендикуляр к плоскости треугольника АВС. Определите вид треугольника АВС, если SC

7)SA-перепендикуляр к плоскости прямоугольника ABCD. Назовите отрезок, изображающий расстояние от точки S до прямой BC

8)Могут ли две прямые, образующие с данной плоскостью равные углы, не быть параллельными ?

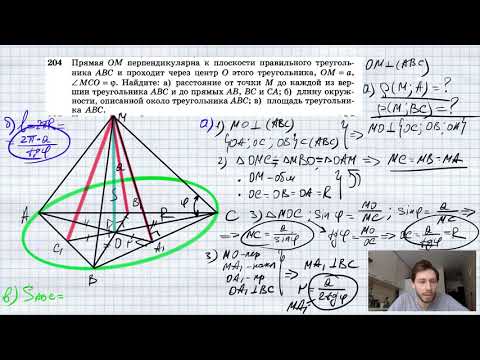
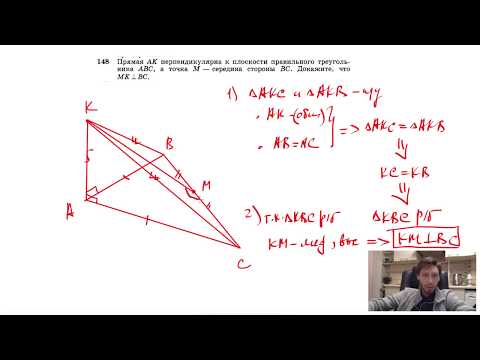
Видео:№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать

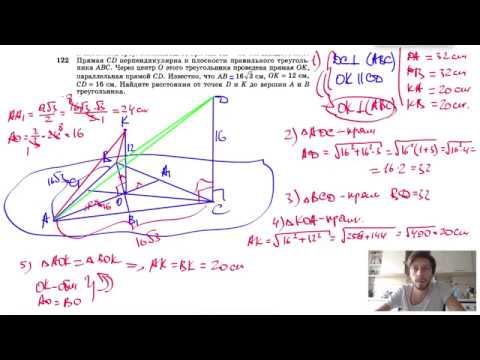
Типовые задачи на применение теоремы о трех перпендикулярах, на угол между прямой и плоскостью

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

К изучению предлагается тема «Типовые задачи на применение теоремы о трех перпендикулярах, на угол между прямой и плоскостью». Вначале мы повторим теорему о трех перпендикулярах, вспомним основные положения теории. Затем вместе с преподавателем решим несколько типовых задач на угол между прямой и плоскостью.

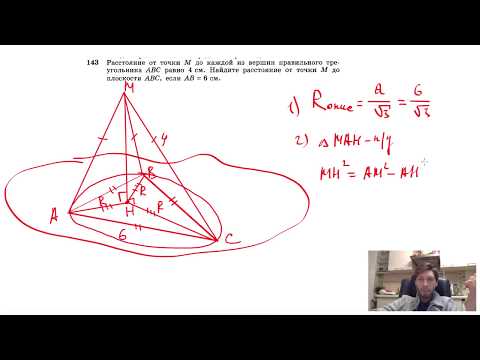
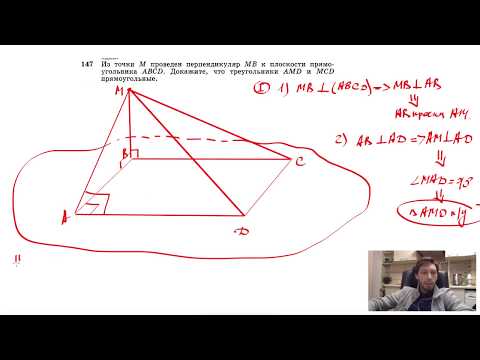
Видео:№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

Перпендикулярность прямой и плоскости. 10-й класс

Класс: 10

Презентация к уроку

Класс: 10.

Базовый учебник: Геометрия 10-11: базовый и профильный уровни/ Л.С. Атанасян и др.- М.: Просвещение, 2009.

К уроку прилагается презентация, тест, сделанный в Microsoft Excel для компьютерной проверки знаний учащихся (Приложение 1), учебный модуль Федерального центра информационно-образовательных ресурсов (Приложение 2),состоящий из 5 заданий различного уровня сложности. Все задания данного модуля параметризованы, что позволяет формировать индивидуальные задания. Задания предназначены для отработки навыков решения задач, используя признак перпендикулярности прямой и плоскости. Для работы с учебным модулем необходимо установить специальную программу, она находится в Приложении 3. В презентации к уроку имеется самостоятельная работа по изучаемой теме. Таким образом, количество предлагаемого материала избыточно, что позволяет его дозировать, варьировать в зависимости от уровня подготовленности класса.

Тип урока: урок творческого применения знаний.

Форма проведения: практикум решения ключевых задач.

Время проведения: 45 минут.

Место урока в разделе: 4 урок.

Цели:

• «открыть» понятия перпендикуляра и наклонной к плоскости;
• формировать умения:
  видеть конфигурации, удовлетворяющие заданным условиям;
  применять определение прямой, перпендикулярной к плоскости, признак перпендикулярности прямой и плоскости к задачам на доказательство;
• выработать навыки решения основных задач на перпендикулярность прямой и плоскости.

• развивать пространственное воображение, логическое мышление;
• развивать самостоятельность учащихся и творческое отношение к выполнению заданий;
• организовать осмысление полученных результатов изучения темы и способов их достижения.

• воспитывать:
  волю и настойчивость для достижения конечных результатов при решении задач;
  информационную культуру и культуру общения.

Методы: частично-поисковый, исследовательский.

Формы организации деятельности: фронтальная, групповая, индивидуальная, самостоятельная работа.

Оборудование: компьютерный класс, мультимедийный проектор, экран, компьютерная презентация по теме, тест (Приложение 1), карточки для индивидуальной работы (Слайд 9), карточки с вопросами теории, ЭОР с практическим параметризованным заданием (Приложение 2).

Видео:Перпендикуляр от точки к плоскостиСкачать

Ход урока

Организационный момент – проверка готовности класса к уроку.

I. Мотивационно-ориентировочная часть.

1. Актуализация знаний.

– Сегодня мы продолжаем работать над темой «Перпендикулярность прямой и плоскости». На прошлых уроках мы «открыли» определение прямой, перпендикулярной к плоскости, признак перпендикулярности прямой и плоскости, разобрали простейшие задачи. В качестве домашнего задания каждый из вас получил лист с вопросами теории, вам предлагалось подготовить ответы на эти вопросы.

Проверим, как вы справились с этим заданием.

Идет фронтальный опрос. (слайды 6-8).

Вопросы:

1. Верно ли утверждение: прямая перпендикулярна к плоскости, если она перпендикулярна к прямой, принадлежащей плоскости? (нет)
2. Могут ли быть перпендикулярны к плоскости две стороны треугольника одновременно? (нет, тогда через одну точку пройдут две прямые, перпендикулярные к плоскости).
3. Сторона AB правильного треугольника ABC лежит в плоскости α. Может ли прямая BC быть перпендикулярна к плоскости α? (нет, так как тогда BC⊥AB, но в правильном треугольнике углы равны 60°).
4. Верно ли утверждение: если прямая перпендикулярна двум прямым, лежащим в плоскости, то она перпендикулярна к данной плоскости? (только если они пересекающиеся).
5. Прямая a перпендикулярна к плоскости α, прямая b не перпендикулярна к плоскости α. Могут ли быть параллельными прямые a и b? (нет, если это предположить, то тогда b⊥a, что противоречит условию).
6. Верно ли утверждение: если прямая перпендикулярна к плоскости, то она перпендикулярна лежащим в этой плоскости двум сторонам треугольника? (нет, она перпендикулярна лежащим в этой плоскости всем трем сторонам треугольника).
7. Через вершину квадрата ABCD проведена прямая AM, перпендикулярная к плоскости квадрата. Докажите, что прямая AD перпендикулярна к плоскости, проходящей через прямые AM и AB.
8. Через центр окружности, описанной около треугольника ABC, проведена прямая, перпендикулярная к плоскости треугольника ABC. Докажите, что каждая точка этой прямой равноудалена от вершин треугольника ABC.
9. На практике вертикальность столба проверяют, глядя на столб поочередно с двух направлений. Как обосновать правильность такой проверки?

Далее повторяются определение прямой, перпендикулярной к плоскости, признак перпендикулярности прямой и плоскости. (Презентация, слайды 3-5).

Подводятся итоги устной работы, оцениваются ответы учащихся.

2. Постановка учебной задачи.

Сегодня мы продолжим формировать умения применять известные утверждения в задачах на доказательство и в решении типовых задач.

II. Содержательная часть.

1. Следующий этап работы – два ученика вызываются к доске для индивидуальной работы по карточкам, с остальными учащимися проводится фронтальная работа по готовым чертежам. Карточки для индивидуальной работы:

Карточка 1

1) прямые AC и D₁O перпендикулярны;

2) ABC₁ = 90°

Карточка 2

Отрезок EF является средней линией прямоугольного треугольника ABC (ACB=90°). Через точку E проведен перпендикуляр ME к плоскости этого треугольника.

Задания для устной работы по готовым рисункам:

Дано: M ABC, MBCD – прямоугольник.

Дано: ABCD – параллелограмм.

Дано: M ABC, ABCD – ромб.

– Ребята, в задачах 4-6 речь идет о наклонных к плоскости. Как вы думаете, что имеется в виду?

Существует ли здесь аналогия с понятиями перпендикуляра и наклонной к прямой, изучаемых в планиметрии?

Учащимся предлагается изучить слайд 10 презентации и решить эти задачи.

2. Работа в парах – решаются задачи по готовым чертежам.

ABC = 90°,

AC = 4, MD = 3.

Решения обсуждаются. Оцениваются ответы отдельных учащихся.

Следующий этап урока – выполнение практического задания на компьютере, работа с ЭОР.

III. Рефлексивно-оценочная часть.

1. Итогом работы на уроке является проверочная работа в форме теста.

Подводятся итоги урока, выставляются оценки.

2. Домашнее задание: № 130, 131, 145, 148. (Указание: использовать признак перпендикулярности прямой и плоскости).

📹 Видео

№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

Перпендикуляр к плоскостиСкачать

Серединный перпендикулярСкачать

Перпендикуляр к плоскостиСкачать

№211. Плоскости правильного треугольника KDM и квадрата KMNP взаимно перпендикулярны. Найдите DN, есСкачать

№148. Прямая АК перпендикулярна к плоскости правильного треугольника ABC, М — середина стороны ВС.Скачать

Построение равнобедренного треугольникаСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

7 класс, 16 урок, Перпендикуляр к прямойСкачать

Перпендикуляр к плоскостиСкачать

№147. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника ABCD. Докажите, чтоСкачать

Перпендикулярность прямой и плоскости. 10 класс.Скачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать