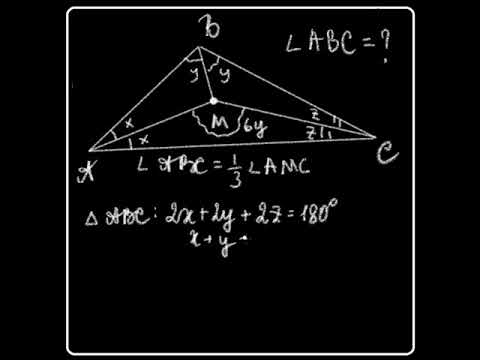
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Свойства сторон и углов треугольника
- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- 🎥 Видео
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Ваш ответ
Видео:Геометрия Стороны треугольника равны 12 см 20 см и 28 см Найдите наибольший угол треугольникаСкачать

решение вопроса
Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Как найти величины углов всех треугольников. Сумма углов треугольника. Геометрия 7 класс.Скачать

Свойства сторон и углов треугольника
| Фигура | Рисунок | Формулировка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длины сторон треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешний угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема косинусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема синусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник | ||||||||||||
 | ||||||||||||
| Большая сторона треугольника | ||||||||||||
 | Против большей стороны треугольника лежит больший угол | |||||||||||
| Больший угол треугольника | ||||||||||||
 | Против большего угла треугольника лежит большая сторона | |||||||||||
| Меньшая сторона треугольника | ||||||||||||
 | Против меньшей стороны треугольника лежит меньший угол | |||||||||||
| Меньший угол треугольника | ||||||||||||
 | Против меньшего угла треугольника лежит меньшая сторона | |||||||||||
| Длины сторон треугольника | ||||||||||||
 | ||||||||||||
| Углы треугольника | ||||||||||||
 | ||||||||||||
| Внешний угол треугольника | ||||||||||||
 | ||||||||||||
| Больший угол треугольника | ||||||||||||
 | ||||||||||||
| Меньший угол треугольника | ||||||||||||
 | ||||||||||||
| Теорема косинусов | ||||||||||||
 | ||||||||||||
| Теорема синусов | ||||||||||||
 | ||||||||||||
| Треугольник |
 |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол

Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона

Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол

Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Свойство углов треугольника:
Сумма углов треугольника равна 180°
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.


Свойство меньшего угла треугольника:

Видео:Хитрая задача от ШарыгинаСкачать

Треугольник. Формулы и свойства треугольников.
Видео:Внешний угол треугольникаСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
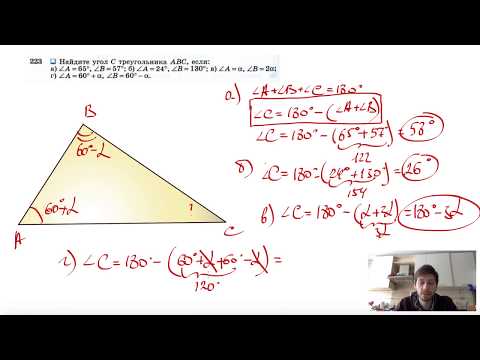
Видео:№223. Найдите угол С треугольника ABC, если: a) ∠A=65°, ∠B = 57°; б) ∠A = 24°, ∠B= 130Скачать
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Сможешь найти угол треугольника?Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

Связь между вписанной и описанной окружностями треугольника
Видео:Внешний угол треугольникаСкачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Геометрия Стороны треугольника равны √18 см 5 см и 7 см Найдите средний по величине уголСкачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
🎥 Видео
Угол треугольника #профильнаяматематика #егэпрофиль #егэ #профиль #артуршарафиевСкачать

Как найти углы в треугольникеСкачать