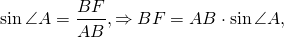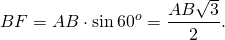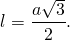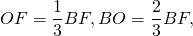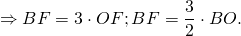Как найти биссектрису равностороннего треугольника (7 видео)

Биссектриса равностороннего треугольника

Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?

(свойство биссектрисы равностороннего треугольника)

В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.

Пусть в треугольнике ABC AB=BC=AC.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

Проведем биссектрису BF.

По свойству равнобедренного треугольника, BF является также его медианой и высотой.

Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.

Что и требовалось доказать .

(свойство биссектрис равностороннего треугольника)

Все три биссектрисы равностороннего треугольника равны между собой.

Пусть в треугольнике ABC AB=BC=AC.

AK, BF CD — биссектрисы треугольника ABC.

В треугольниках ABF, BCD и CAK:

AB=BC=CA (по условию)
∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).

Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.

Что и требовалось доказать .

Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.

1) Найдём биссектрису равностороннего треугольника через его сторону.

В треугольнике ABC AB=BC=AC=a.

BF — биссектриса, BF=l.

По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.

Из прямоугольного треугольника ABF по определению синуса

Таким образом, формула биссектрисы равностороннего треугольника по его стороне:

2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.

В правильном треугольнике ABC центры вписанной и описанной окружностей совпадают.

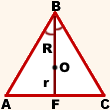
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.

Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.

Таким образом, длина биссектрисы через радиус вписанной окружности равна

Содержание

Найти медиану биссектрису высоту равностороннего треугольника
Свойства биссектрисы равностороннего треугольника
Свойства биссектрисы равностороннего треугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Свойство 6
Свойство 7
Пример задачи
🌟 Видео

Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Найти медиану биссектрису высоту равностороннего треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L — высота=биссектриса=медиана

a — сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):

Калькулятор — вычислить, найти медиану, биссектрису, высоту

Видео:Задание 9 ОГЭ от ФИПИСкачать

Свойства биссектрисы равностороннего треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Свойства биссектрисы равностороннего треугольника

Свойство 1

Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.

BD – биссектриса угла ABC, которая также является:

высотой, опущенной на сторону AC;
медианой, делящей сторону AC на два равных отрезка (AD = DC);

Свойство 2

Все три биссектрисы равностороннего треугольника равны между собой.

Свойство 3

Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.

Свойство 4

Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.

r – радиус вписанной окружности;
R – радиус описанной окружности;
R = 2r.

Свойство 5

Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.

Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.

Свойство 6

Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.

AD и AE – внешние биссектрисы, параллельные BC;
BK и BL – внешние биссектрисы, параллельные AC;
CM и CN – внешние биссектрисы, параллельные AB.

Свойство 7

Длину биссектрисы ( l_a ) равностороннего треугольника можно выразить через его сторону.

где a – сторона треугольника.

Видео:Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Пример задачи

Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.

Решение

Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).

Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):