Как сравнивать углы треугольника (7 видео)

Сравнение углов

Сравнить два угла — это значить узнать, какой из углов больше, какой меньше, или определить, что углы равны.

Сравнить углы можно двумя способами: наложением или измерением их величин.

Содержание

Сравнение наложением
Сравнение измерением
Геометрия. 7 класс
Треугольник. Соотношения между углами и сторонами треугольника.
📸 Видео

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Сравнение наложением

Рассмотрим, как сравнивать углы путём наложения. Дано два угла, ∠BOA и ∠COA:

Чтобы выяснить, равны они или нет, наложим один угол на другой так, чтобы вершина одного угла совпала с вершиной другого угла и сторона одного угла совместилась со стороной другого:

Мы видим, что ∠СOA составляет часть ∠BOA, поэтому ∠СOA меньше ∠BOA, это записывают так:

Если при наложении углов обе их стороны совмещаются, то углы равны.

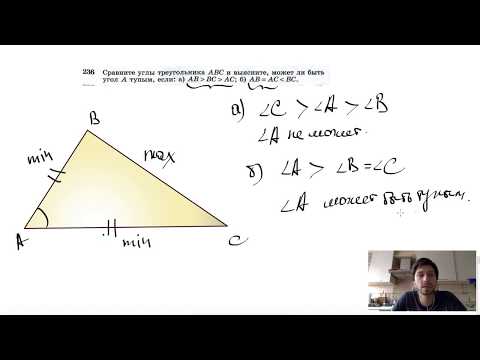
Видео:№236. Сравните углы треугольника ABC и выясните, может ли быть угол А тупым, если: а) АВСкачать

Сравнение измерением

При сравнении углов путём измерения их величин больше будет тот угол, у которого больше величина.

Пример. Сравнить два угла: ∠BOC и ∠MON.

Так как величина ∠BOC (60°) меньше, чем величина ∠MON (70°), то

Видео:Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Геометрия. 7 класс

Конспект урока

Соотношения между сторонами и углами треугольника. Неравенство треугольника

Перечень рассматриваемых вопросов:

Установление соотношений между сторонами и углами треугольника.
Формулирование неравенства треугольника.
Теоремы о сравнении сторон и углов треугольника, их применение при решении задач.
Проведение исследования о существовании треугольника с заданными элементами.

Каждая сторона треугольника меньше суммы двух других сторон.

В треугольнике против большей стороны лежит больший угол. Против большего угла лежит большая сторона.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее, на уроках геометрии, вы познакомились с различными фигурами, в том числе и с треугольником.

Сегодня мы продолжим изучать треугольники и рассмотрим соотношение между его элементами.

Теорема: В треугольнике против большей стороны лежит больший угол.

Отложим на стороне AB отрезок, равный стороне AC.

Угол 2 – внешний угол треугольника BDC, поэтому ∠2 > ∠B (по свойству внешнего угла треугольника).

∠1 = ∠2 как углы при основании равнобедренного ∆ADC (по свойству равнобедренного треугольника).

Справедлива и теорема, обратная данной. Против большего угла лежит большая сторона.

Предположим, что АВ = АС или АВ ∠ В.

Поэтому наше предположение неверное → AB > AC.

Докажем два следствия из этих теорем.

1 следствие. В прямоугольном треугольнике гипотенуза больше катета.

Дано: ∆АВС – прямоугольный.

Доказательство: ∠В > ∠А, т. к. ∠В = 90° ( по условию), ∠А –острый → АС > СВ (по обратной теореме о соотношениях между сторонами и углами треугольника: против большего угла лежит большая сторона).

Что и требовалось доказать.

Докажем второе следствие из этих теорем.

Если два угла треугольника равны, то треугольник равнобедренный. Это следствие называется признак равнобедренного треугольника.

Доказать: ∆АВС – равнобедренный

Докажем, что АВ = ВС.

Пусть АВ > ВС →∠С > ∠А (по теореме доказанной выше: против большей стороны лежит больший угол), противоречит условию, т. к. ∠А = ∠С . → АВ = ВС →∆АВС – равнобедренный (по определению равнобедренного треугольника).

Что и требовалось доказать.

Докажем теорему по соотношению между сторонами треугольника.

Каждая сторона треугольника меньше суммы двух других сторон.

Доказать: АВ ∠1 (так как угол 1 часть угла АВD), →∠ABD > ∠2 (так как ∠1 = ∠2).

Так как против большего угла лежит большая сторона (по теореме о соотношениях между сторонами и углами треугольника) → AB ВН (по обратной теореме о соотношениях между сторонами и углами треугольника).

Рассмотрим ещё случай АВ = ВС → ∆АВС – равнобедренный (по определению равнобедренного треугольника). То ВМ = ВН (по свойству равнобедренного треуголника, высота и медиана совпадают, если проведены к его основанию)→ ВМ ≥ ВН.

Что и требовалось доказать.

Разбор заданий тренировочного модуля.

1 Дано: ABC, равнобедренный, вычислите чему равна третья сторона треугольника, если две других равны 8 см и 4 см?

Объяснение: По определению равнобедренного треугольника, две его боковые стороны равны, следовательно это будет сторона равная 4 см или 8см.

Сторона 4см не может быть, т. к. 8см = 4 см + 4 см., что противоречит теореме о соотношениях между сторонами треугольника: каждая сторона треугольника меньше суммы двух других сторон.

Предположим, что боковые стороны равны 8 см. Тогда, по теореме о соотношениях между сторонами треугольника, каждая сторона треугольника меньше суммы двух других сторон, получим следующее соотношение между сторонами треугольника:

Видео:Геометрия 7 класс (Урок№3 - Сравнение отрезков и углов.)Скачать

Треугольник. Соотношения между углами и сторонами треугольника.

Теорема.

Если любую сторону треугольника продолжить в одном направлении, то образовавшийся при этом внешний угол больше каждого внутреннего угла, не смежного с ним.

Следствие из теоремы.

Если в треугольнике один из углов прямой или тупой, то два других угла будут острые.

Теорема. В любом треугольнике:

1. Напротив равных сторон расположены одинаковые углы.

2. Напротив большей стороны расположен больший угол.

Следствия из теоремы.

2. В разностороннем треугольнике одинаковых углов нет.

Обратные теоремы. В каждом треугольнике:

1. Напротив одинаковых углов расположены одинаковые стороны.

2. Напротив большего угла расположена большая сторона.

Следствия

1. Равноугольный треугольник является и равносторонним.