Системой сил = (Рис.4).называется множество сил, приложенных к точкам механической системы.
Главным вектором системы сил называется векторная сумма всех сил системы:
Найти главный вектор можно, построив в произвольном центре О векторный многоугольник, в котором начало последующей силы совпадает с концом предыдущей (рис.4). Замыкающая сторона многоугольника и есть главный вектор V системы сил.
Для пространственной системы сил построить многоугольник практически трудно. Проще найти главный вектор аналитически. Проектируя слагаемые формулу (6) на оси координат, определим проекции главного вектора, его модуль и направляющие косинусы:
Vx=Fkx; Vy=Fky; Vz=Fkz (7)
V2=Vx2+Vy2+Vz2; Cos(V,x)=Vx/V; Cos(V,y)=Vy/V; Cos(V,z)=Vz/V
Момент силы относительно точки. Теоремы о моменте
Пусть сила F приложена в точке А тела, имеющей радиус-вектор r относительно центра О.
Моментом силы F относительно центра О называется вектор
Направление векторного произведения усдовно и зависит от ориентированности пространства. Ориентированность пространства- это принятое нами правило соответствия прямой и дуговой стрелок: правого или левого винта. Вектора, направление которых зависит от оринтированности пространства, называются аксиальными. Важно, что для них (Рис.5) дуговая стрелка составляет физическую сущность (показывает направление вращения) а направление самого вектора условено.
Мы будем работать в право ориентированном пространстве и направление векторного произведения всегда будем определять пл правилу правого винта: с конца mo видно , что сила стремится повернуть тело против часовой стрелки.
Модуль момента равен произведению модуля силы на плечо h -длину перпендикуляра, опущенного из центра О на линию действия силы.
Очевидно, что момент силы тем меньше, чем меньше ее плечо, и он обращается в ноль для любого центра на линии действия силы. Вы это ощущаете, поднимая воротом ведро из колодца, и поэтому стараетесь приложить силу руки так, чтобы создать большее плечо. Из формулы для модуля момента ясно, что момент силы равен нулю только относительно точки, лежащей на линии действия силы.
Теорема 1. О зависимости момента от центра
Рис.6 а) в общем случае момент силы зависит от центра б) перенос центра параллельно линии действия силы не изменяет момента
Найдем связь между моментами силы F относительно центров А и В. Из Рис.6 ясно, что
rA= AB+rB mA(F)=rAxF=(AB+rB)xF= rBxF +ABxF
Теорема 2. О проекциях моментов.
Проектируя (10) на ось z, проходящую через А и В, находим
Таким образом приходим к лемме:
поскольку произведение АВ Х F перпендикулярно АВ и его проекция на z равна нулю. Проекции моментов силы относительно всех точек одной оси на эту ось равны между собой. Таким образом проекция моментов на ось характеризует действие силы по отношению к этой оси, поэтому называется моментом сил относительно. Матричное вычисление векторного произведения (момента). Присоединенная матрица. Известно, что векторное произведение можно представить в виде определителя матрицы
c=a x b == (aFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k (12)
mo(F)=r x F== (yFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k
Здесь i, j, k — орты осей x, y, z с началом в центре О, x, y, z — проекции радиуса-вектора r на эти оси.
В матричной алгебре вектору соответствует столбец его проекций на декартовы оси.
Таким образом вектор-столбец момента имеет вид
Легко убедится, что этот же результат можно получить, умножив кососимметричную матрицу, составленную из элементов столбца r
на вектор-столбец сил F (1).
Матрица R называется присоединенной матрицей вектора r
В общем случае столбец проекций векторного произведения c=a b удобно находить через присоединенную кососимметричную матрицу первого сомножителя часовой стрелки
Видео:Система сходящихся сил. Решение задач по МещерскомуСкачать

Найти главный вектор системы сил f1 3h f2 4h f3 10h a 30
2. Плоская система сил.
2.2 Главный вектор и главный момент плоской системы сил.
Приведение к простейшему виду.
2.2.1. Определить главный вектор плоской системы сил, если заданы его проекции на координатные оси Rx = 300Н, Rу = 400Н. (Ответ 500)
2.2.2. Определить главный момент системы двух сил относительно точки А, если силы G = 1Н, F = 5Н, расстояние l = 0,2 м, угол φ = 60°. (Ответ -0,916)
2.2.3. К вершинам квадрата приложены четыре силы F1 = F2 = F3 = F4 = 1Н. Определить модуль равнодействующей этой системы сил. (Ответ 2,0)
2.2.4. За центр приведения данной системы сил выбрана точка, расположенная на оси Оу, в которой главный момент равен нулю. Определить ординату этой точки, если силы
F1 = F2 = F3 = 1Н, F4 = 2Н, радиус r = 1 м. (Ответ -1,0)
2.2.5. К вершинам равностороннего треугольника приложены силы F1 = F2 = F3 = 1Н.
Определить модуль равнодействующей этой системы сил. (Ответ 1,0)
2.2.6. Заданы силы F1 = F2 = F3 = 12H, F4 = 14Н. Определить главный момент заданной плоской системы сил относительно точки О, если радиус r = 0,2 м. (Ответ 0,233)
2.2.7. К вершинам прямоугольного треугольника приложены три силы.
Определить значение угла α в градусах, при котором главный момент данной системы си л
М 0 = -2 кН•м, если сила F2=4 кН, расстояние l = 1 м. (Ответ 30,0)
2.2.8. К вершинам прямоугольного треугольника приложены силы F1 = 3Н, F2 = 6Н, F3 = 14Н. Определить значение угла а в градусах, при котором главный вектор данной системы сил параллелен оси Ох (Ответ 30,0)
2.2.9. К прямоугольнику приложены четыре силы по 10Н каждая. Определить модуль главного вектора заданной системы сил, если угол α = 60°. (Ответ 22,4)
2.2.10. К квадрату приложены шесть сил по 6Н каждая. Определить главный момент заданной плоской системы сил относительно точки А, если расстояние l = 0,5 м. (Ответ 8,48)
2.2.11. К вершинам квадрата приложены шесть сил по 4Н каждая. Определить главный момент заданной плоской системы сил относительно точки B, если расстояние l = 0,4 м. (Ответ 4,99)
2.2.12. К вершинам прямоугольного треугольника приложены силы F1 = 12Н, F2 = 4Н, F3 = 2Н. Определить значение угла α в градусах, при котором главный вектор данной системы сил параллелен оси Оу. (Ответ 60,0)
2.2.13. К прямоугольнику приложены силы F1 = 4Н, F2 = 5Н, F3 = 8Н, F4 = 2Н. Определить главный момент заданной системы сил относительно точки А, если расстояние l = 1 м, угол α = 30°. (Ответ 6,89)
2.2.14. К правильному шестиугольнику приложены пять равных по модулю сил. Определить в градусах угол между главным вектором этой системы сил и осью Ох. (Ответ 180)
2.2.15. Задана плоская система сил F1 = F2 = F3 = 2H, F4 = 10Н. Определить главный момент лой системы сил относительно точки А, если радиус r = 1 м. (Ответ 11,3)
2.2.16. При каком значении угла α равнодействующая системы трех сил будет направлена вертикально, если силы F1 = 3,46Н, F2 = 2Н, F3 = 4Н? (Ответ 60,0)
2.2.17. Задана плоская система сил F1 = F2 = F3= F4 = 4Н, F5 = 5Н. Определить модуль главного вектора этой системы сил. (Ответ 5,0)
2.2.18. На каком кратчайшем расстоянии oт точки А проходит линия действия равнодействующей системы четырех сил, если F1 = F2 =F3 = F4 = 1H, расстояние l = 0,1 м? (Ответ 0.05)
2.2.19. На каком расстоянии d нужно приложить силу F = 100Н, для того чтобы линия
действия равнодействующей этой силы и распределенной нагрузки интенсивностью
qmax = 3 Н/м прошла через точку А, если расстояние l = 10м, угол α = 60°? (Ответ 4,0)
2.2.20. Какой угол в градусах с осью Ох составляет равнодействующая системы сил,
если F1 = F2 = F3 = F4? (Ответ 45,0)
2.2.21. К квадрату приложена система четырех сил, причем силы F1 = F2 = F3 = 1Н.
Определить модуль силы F4, при которой равнодействующая системы R = 2Н. (Ответ 1,0)
Видео:определение реакций в стержнях от действия грузовСкачать

Контрольная работа по Теоретической механике
по Теоретической механике
для студентов 1 курса ФМиЕНО
Направление подготовки 15.03.01 Машиностроение
Профиль подготовки: Технологии, оборудование и автоматизация машиностроительных производств
Для успешного написания контрольной работы необходима определенная подготовка. Подготовку контрольной работы следует начинать с повторения соответствующего раздела учебника, учебных пособий по данной теме и конспектов лекций прочитанных ранее.
Контрольная работа выполняется студентами по индивидуальным вариантам. Вариант выбирается по последней цифре номера зачетной книжки (студенческого билета). Например: если эта цифра «1», вариант под номером «1» и т. д., цифре «0» соответствует вариант под номером «10».
Контрольная работа выполняется в отдельной тетради или на листах формата А4, страницы нумеруются. На обложке указываются: название дисциплины, фамилия и инициалы студента, факультет, направление и профиль подготовки, курс обучения, вариант контрольной работы. Работы могут быть представлены как в рукописном, так и в печатном исполнении.
Решение каждой задачи следует начинать с новой страницы. Сначала необходимо переписать полностью условие задачи, далее делается расчетная схема, записываются исходные данные и искомые величины. Расчетная схема выполняется с учетом данных решаемого варианта задачи: все углы, действующие силы, число сил и их расположение на рисунке должны соответствовать этим условиям. Решение каждой задачи необходимо сопровождать краткими пояснениями, какие аксиомы, теоремы или законы используются для решения; какие математические преобразования приводят к результату и т. п. Студентам необходимо подробно излагать весь ход расчетов, указывая единицы измерения получаемых величин.
Равнодействующая R двух равных по модулю сходящихся сил F1 = F2 = 15 H направлена по оси Оy и равна по модулю 10 Н. Определить в градусах угол б, образованный вектором силы F2 с положительным направлением оси Оx.
На балку АВ действуют силы F = 9 Н и распределенная нагрузка интенсивностью q =3 кН/м. Определить реакцию опоры В, если длины
АВ = 5 м, ВС = 2 м.
При каком значении угла б равнодействующая системы трех сил будет направлена вертикально, если силы F1 = 3,46 Н, F2 = 2 Н, F3 = 4 Н?
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая сходящихся сил F1 и F2 равна по модулю R = 40 Н и образует с горизонтальной осью Оx угол б = 25°. Вектор силы F1 направлен по оси Оx, а вектор силы F2 образует с этой осью угол в = 50°. Определить модуль силы F1. Какой должна быть длина участка АС с действующей на него распределенной нагрузкой интенсивностью q = 5 кН/м, для того чтобы реакция опоры В была равна 10 кН, если длина балки АВ = 9 м? 
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая R двух равных по модулю сходящихся сил F1 = F2 = 20 H направлена по оси Оy и равна по модулю 15 Н. Определить в градусах угол б, образованный вектором силы F2 с положительным направлением оси Оx.
Определить реакцию опоры С, если интенсивность распределенной нагрузки qmах = 120 Н/м, размеры АВ = 4,5 м, ВС = 1,5 м.
К прямоугольнику приложены силы F1 = 4 H, F2 = 5 H, F3 = 8 H, F4 = 2 H. Определить главный момент заданной системы сил относительно точки А, если расстояние l = 1м, угол б = 30°.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая сходящихся сил F1 и F2 равна по модулю R = 25 Н и образует с горизонтальной осью Оx угол б = 30°. Вектор силы F1 направлен по оси Оx, а вектор силы F2 образует с этой осью угол в = 60°. Определить модуль силы F1. Определить реакцию опоры В, если интенсивность распределенной нагрузки q = 40 Н/м, размеры балки АВ = 4 м, ВС = 2 м.
К вершинам прямоугольного треугольника приложены силы F1 = 12 Н, F2 = 4 Н, F3 = 2 Н. Определить значение угла б в градусах, при котором главный вектор данной системы сил параллелен оси Оу.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая R двух равных по модулю сходящихся сил F1 = F2 = 10 H направлена по оси Оy и равна по модулю 18 Н. Определить в градусах угол б, образованный вектором силы F2 с положительным направлением оси Оx.
Какой должна быть интенсивность qmax распределенной нагрузки, для того чтобы реакция опоры В равнялась 200 Н, если размеры АС = 2 м, CD = 3 м, DB = 1 м?
К прямоугольнику приложены четыре силы по 10 Н каждая. Определить модуль главного вектора заданной системы сил, если угол а = 60°.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая сходящихся сил F1 и F2 равна по модулю R = 12 Н и образует с горизонтальной осью Оx угол б = 20°. Вектор силы F1 направлен по оси Оx, а вектор силы F2 образует с этой осью угол в = 40°. Определить модуль силы F1. Определить модуль силы F при которой момент в заделке А равен 300 Н·м, если интенсивноcть распределенной нагрузки qmax = 20 Н/м, а размеры АВ = 1 м, ВС = 2 м, CD = 3 м.
К вершинам прямоугольного треугольника приложены силы F1 = 3 Н, F2 = 6 Н, F3 = 14 Н. Определить значение угла а в градусах, при котором главный вектор данной системы сил параллелен оси Ох.
Определить реакции в шарнирных опорах балки.
Равнодействующая R двух равных по модулю сходящихся сил F1 = F2 = 12 H направлена по оси Оy и равна по модулю 15 Н. Определить в градусах угол б, образованный вектором силы F2 с положительным направлением оси Оx.
На балку АВ действуют силы F = 12 Н и распределенная нагрузка интенсивностью q =4 кН/м. Определить реакцию опоры В, если длины АВ = 10 м, ВС = 4 м.
К вершинам прямоугольного треугольника приложены три силы. Определить значение угла а в градусах, при котором главный момент данной системы сил МO = 2 кН·м, если сила F2 = 4 кН, расстояние l = 1 м.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая сходящихся сил F1 и F2 равна по модулю R = 10 Н и образует с горизонтальной осью Оx угол б = 45°. Вектор силы F1 направлен по оси Оx, а вектор силы F2 образует с этой осью угол в = 90°. Определить модуль силы F1. Определить реакцию опоры С, если интенсивность распределенной нагрузки qmах = 60 Н/м, размеры АВ = 9 м, ВС = 3 м.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая R двух равных по модулю сходящихся сил F1 = F2 = 8 H направлена по оси Оy и равна по модулю 12 Н. Определить в градусах угол б, образованный вектором силы F2 с положительным направлением оси Оx.
Определить модуль силы F при которой момент в заделке А равен 400 Н·м, если интенсивноcть распределенной нагрузки qmax = 30 Н/м, а размеры АВ = 2 м, ВС = 4 м, CD = 6 м.
За центр приведения данной системы сил выбрана точка, расположенная на оси Оу, в которой главный момент равен нулю. Определить ординату этой точки, если силы F1 = F2 = F3 = 1 Н, F4 = 2 Н, радиус г = 1 м.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
Равнодействующая сходящихся сил F1 и F2 равна по модулю R = 8 Н и образует с горизонтальной осью Оx угол б = 30°. Вектор силы F1 направлен по оси Оx, а вектор силы F2 образует с этой осью угол в = 60°. Определить модуль силы F1. Какой должна быть интенсивность qmax распределенной нагрузки, для того чтобы реакция опоры В равнялась 400 Н, если размеры АС = 6 м, CD = 9 м, DB = 3 м?
Определить главный момент системы двух сил относительно точки А, если силы G = 1 Н, F = 5 Н, расстояние l = 0,2 м, угол ц = 60°.
Невесомая горизонтальная балка покоится на двух шарнирных опорах, одна из которых неподвижная, а другая подвижная. На горизонтальную балку действует сосредоточенная сила 




Определить реакции в шарнирных опорах балки.
📽️ Видео
Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Векторное уравнение движения. Условие столкновения частиц: Иродов 1.5Скачать

Как решить любую задачу по механике. АлгоритмСкачать

Как на графике указать результаты измерений с учетом погрешности?Скачать

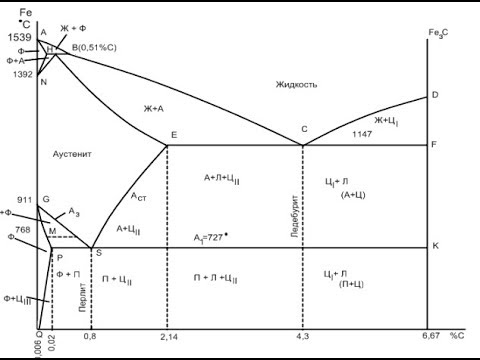
ДИАГРАММА СОСТОЯНИЯ ЖЕЛЕЗО-ЦЕМЕНТИТ, железо-углерод, Fe+Fe3CСкачать
Техническая механика | Равнодействующая сил | Аналитический метод | Теорема ПифагораСкачать

Решение примеров на формулы понижения степени. Как решать? Тригонометрия 10 класс. Видеоурок #22Скачать

Форш П. А. - Теоретическая механика - Формализм Лагранжа. Уравнения Лагранжа для материальной точкиСкачать

Статика С1, С3Скачать

Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Как снять векторную диаграммуСкачать