Дан треугольник авс и вектор а построить фигуру f на которую отображается данный треугольник (4 видео)

На рисунке даны прямая а и треугольник ABC. Постройте фигуру F, на которую отображается данный треугольник при осевой симметрии с осью а

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
§ 2. Параллельный перенос и поворот
Параллельный перенос
Поворот
Задачи
📸 Видео

Видео:№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать

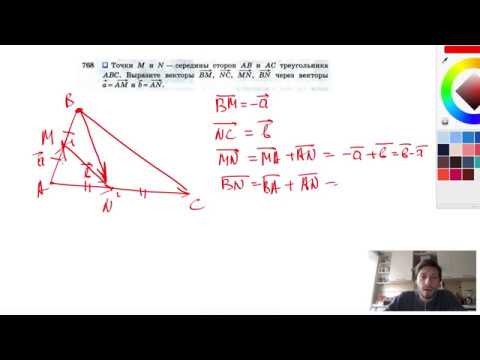
Ваш ответ

Видео:№767. Дан треугольник ABC. Выразите через векторы а=АВ и b=АС следующие векторы:Скачать

решение вопроса

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

§ 2. Параллельный перенос и поворот

Параллельный перенос

Пусть — данный вектор. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что вектор равен вектору (рис. 329).

Параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояния. Докажем это. Пусть при параллельном переносе на вектор точки М и N отображаются в точки М₁ и N₁ (см. рис. 329). Так как , то . Отсюда следует, что ММ₁ || NN₁ и MM₁ = NN₁, поэтому четырёхугольник MM₁N₁N — параллелограмм. Следовательно, MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М₁ и N₁ (случаи, когда точки М и N расположены на прямой, параллельной вектору , рассмотрите самостоятельно). Таким образом, параллельный перенос сохраняет расстояния между точками и поэтому представляет собой движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

Поворот

Отметим на плоскости точку О (центр поворота) и зададим угол а (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α (рис. 330). При этом точка О остаётся на месте, т. е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении — по часовой стрелке или против часовой стрелки. На рисунке 330 изображён поворот против часовой стрелки.

Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.

Докажем это. Пусть О — центр поворота, α — угол поворота против часовой стрелки (случай поворота по часовой стрелке рассматривается аналогично). Допустим, что при этом повороте точки М и N отображаются в точки М₁ и N₁ (рис. 331). Треугольники OMN и ОМ₁N₁ равны по двум сторонам и углу между ними: ОМ = ОМ₁, ON = ON₁ и ∠MON = ∠M₁ON₁ (для случая, изображённого на рисунке 331, каждый из этих углов равен сумме угла α и угла M₁ON). Из равенства этих треугольников следует, что MN = M₁N₁, т. е. расстояние между точками М и N равно расстоянию между точками М, и N, (случай, когда точки О, М и N расположены на одной прямой, рассмотрите самостоятельно). Итак, поворот сохраняет расстояния между точками и поэтому представляет собой движение. Это движение можно представить себе как поворот всей плоскости вокруг данной точки О на данный угол α.

Задачи

1162. Начертите отрезок АВ и вектор . Постройте отрезок А1В1, который получается из отрезка АВ параллельным переносом на вектор .

1163. Начертите треугольник АВС, вектор , который не параллелен ни одной из сторон треугольника, и вектор , паралдельный стороне АС. Постройте треугольник А₁В₁С₁, который получается из треугольника АВС параллельным переносом: а) на вектор ; б) на вектор .

1164. Даны равнобедренный треугольник АВС с основанием АС и такая точка D на прямой АС, что точка С лежит на отрезке AD. а) Постройте отрезок BlD, который получается из отрезка ВС параллельным переносом на вектор . б) Докажите, что четырёхугольник ABB₁D — равнобедренная трапеция.

1165. Даны треугольник, трапеция и окружность. Постройте фигуры, которые получаются из этих фигур параллельным переносом на данный вектор .

1166. Постройте отрезок А₁В₁, который получается из данного отрезка АВ поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на 75° против часовой стрелки; в) на 180°.

1167. Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки А на угол 150° против часовой стрелки.

1168. Точка D является точкой пересечения биссектрис равностороннего треугольника АВС. Докажите, что при повороте вокруг точки D на угол 120° треугольник АВС отображается на себя.

1169. Докажите, что при повороте квадрата вокруг точки пересечения его диагоналей на угол 90° квадрат отображается на себя.

1170. Постройте окружность, которая получается из данной окружности с центром С поворотом вокруг точки О на угол 60° против часовой стрелки, если: а) точки О и С не совпадают; б) точки О и С совпадают.

1171. Постройте прямую а₁, которая получается из данной прямой а поворотом вокруг точки О на угол 60° по часовой стрелке, если прямая а: а) не проходит через точку О; б) проходит через точку О.

а) Построим окружность с центром О, которая касается прямой а (объясните, как это сделать). Пусть М — точка касания. При повороте вокруг точки О эта окружность отображается на себя, а касательная а отображается на некоторую касательную а₁ (объясните почему). Для построения прямой ах построим сначала точку М₁, в которую отображается точка М при повороте вокруг точки О на угол 60° по часовой стрелке, а затем проведём касательную а₁ к окружности в точке М₁.