Какое утверждение неверное если одна из двух параллельных прямых пересекает данную (6 видео)

Какое утверждение неверное если одна из двух параллельных прямых пересекает данную

1.выберете верное утверждение:

а) если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая также параллельна данной плоскости.

б) если одна из двух параллельных прямых пересекает данную плоскость, то другая прямая также пересекает эту плоскость.

в) если две прямые параллельны третьей прямой, то они пересекаются

г) если прямая и плоскость не имеют общих точек, то прямая лежит в плоскости

д) прямая и плоскость называются скрещивающимися, если они не имеют общих точек

Видео:Параллельность прямых. 10 класс.Скачать

Теорема 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

ПЛАН ЗАНЯТИЯ № 25

Дисциплина: Математика

Тема: Параллельность прямой и плоскости

Цель занятия: ввести понятия параллельности прямой и плоскости; изучить признак параллельности прямой и плоскости; обобщить и систематизировать знания о взаимном расположении прямой и плоскости.

Планируемые результаты

Предметные:формировать умения и навыки читать и строить чертежи пространственных конфигураций, пространственных фигур к задачам.

Метапредметные: развивать пространственное воображение при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность, математическую речь, память, внимание;

Личностные: овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

Норма времени:2 часа

Вид занятия:Лекция информационная + решение задач

План занятия:

1. Параллельность прямых

2. Параллельность прямой и плоскости

Оснащение: Мультимедийная доска

Литература:Башмаков М.И. Математика: Алгебра и начала анализа и геометрия. Рек. ФГАУ «ФИРО». М.: Академия, 2017. Занятие 3, с.40-45.

Преподаватель: Сулейманов Р.Р.

Тема Параллельность в пространстве

1. Параллельность прямых

2. Параллельность прямой и плоскости

Параллельные прямые в пространстве

Определение

Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются.

Параллельность прямых a и b обозначается так: a∥b илиb∥a.

Teорема 1. Через две параллельные прямые можно провести плоскость, и при том только одну.

Доказательство:

1. Так как прямые a и b параллельны, из определения следует, что через них можно провести плоскость α.

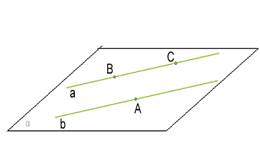
2. Чтобы доказать, что такая плоскость только одна, на прямой a обозначаем точки B и C, а на прямой b точку A.

3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость (2 аксиома), то α является единственной плоскостью, которой принадлежат прямые a и b.

Теорема 2. Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и при том только одну.

Доказательство:

1. Через данную прямую a и точку M, которая не лежит на прямой, проводится плоскость α.

2. Такая плоскость только одна (т.к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).

3. А в плоскости α через точку M можно провести только одну прямую b, которая параллельна прямой a.

Теорема 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Геометрия. 10 класс

Параллельность прямых, прямой и плоскости

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Существует еще два утверждения, которые используют при решении задач:

1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.