Задание 26. Середина М стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 6, а углы В и С четырёхугольника равны соответственно 124° и 116°.
В четырехугольнике ABCD точка M – середина AD и равноудалена от вершин A, B, C и D. Следовательно, AM=MD=MB=MC.
Пусть 

Учитывая, что сумма углов в любом треугольнике 180 градусов, имеем:
Рассмотрим треугольник BMC, в котором сумма углов равна
и треугольник BMC – равносторонний. Поэтому BM=BC=6 и AM=BM=6. Тогда сторона AD=2AM=2∙6=12.
- В выпуклом четырёхугольнике ABCD точка K — середина AB, точка L — середина BC, точка M — середина CD, точка N — середина DA?
- Диагонали квадрата ABCD пересекаются в точке O, точка F — середина стороны CD, а точка T лежит на стороне AD и TF / / AC?
- Биссектрисы A и D параллелограма ABCD пересекаются в точке E стороны BC?
- Точки M и H — середины боковых сторон AB и CD трапеции ABCD?
- Точка M середина стороны AB треугольника ABC, точка K середина стороны AC?
- Даю 35 БАЛОВ ?
- Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке N лежащей на стороне CD докажите что N середина CD?
- Биссектрисы углов А и В параллелограмма АВСD пересекаются в точке N лежащей на стороне CD докажите что N середина CD?
- Угл А = углуВ = 90градусов точка О — середина АВ докажите что точка О — середина СД?
- В прямоугольнике ABCD точка M — середина BC?
- ABCD — параллелограмм, точки M и K — середины сторон AB и BC соответственно (задание во вложении)?
- Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 📽️ Видео
Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

В выпуклом четырёхугольнике ABCD точка K — середина AB, точка L — середина BC, точка M — середина CD, точка N — середина DA?
Геометрия | 5 — 9 классы
В выпуклом четырёхугольнике ABCD точка K — середина AB, точка L — середина BC, точка M — середина CD, точка N — середина DA.
Для некоторой точки S, лежащей внутри четырёхугольника ABCD, оказалось, что KS = LS и NS = MS.
Докажите, что угол KSN = углу MSL.
По условиючтокл — средняя линия треугольника DAB, а NM средняя линия треугольника BCD, поэтому прямые KL, DB и MN – параллельны.
Аналогично параллельны прямые, BM, AC и KN.
Поэтому KLMN – параллелограммтак как KL и DB, KN и ВС соответственно параллельны, то угол ВKN = 30 гр.
S = 8 * 14 * sin(30) = 56.
Видео:Геометрия Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершинСкачать

Диагонали квадрата ABCD пересекаются в точке O, точка F — середина стороны CD, а точка T лежит на стороне AD и TF / / AC?
Диагонали квадрата ABCD пересекаются в точке O, точка F — середина стороны CD, а точка T лежит на стороне AD и TF / / AC.
Вычислите площадь четырёхугольника AOFT, если AB = 6 см.
Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Биссектрисы A и D параллелограма ABCD пересекаются в точке E стороны BC?
Биссектрисы A и D параллелограма ABCD пересекаются в точке E стороны BC.
Докажите, что E — середина BC.
Видео:Геометрия Четырехугольник оказался вписанным Задача №26 ОГЭСкачать

Точки M и H — середины боковых сторон AB и CD трапеции ABCD?
Точки M и H — середины боковых сторон AB и CD трапеции ABCD.
Точка P не лежит в плоскости этой трапеции.
Докажите, что прямая BC параллельна плоскости MPH.
Видео:🔴 В параллелограмме ABCD отмечена точка M ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать
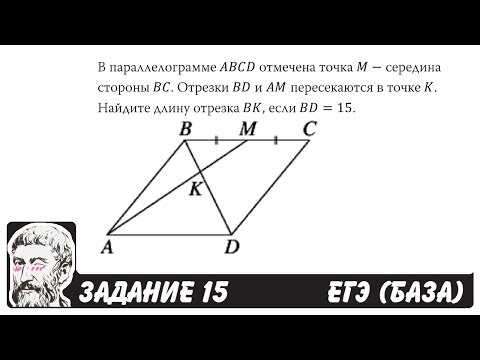
Точка M середина стороны AB треугольника ABC, точка K середина стороны AC?
Точка M середина стороны AB треугольника ABC, точка K середина стороны AC.
Площадь AMK равна 12 см квадратных.
Чему равна площадь четырёхугольника BMKC?
Видео:Геометрия Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можноСкачать

Даю 35 БАЛОВ ?
В прямоугольнике ABCD BC = 10 см Точка T — внутренняя точка отрезка BC .
В четырёхугольнике ATCD вписана окружнасть .
Извесно , что расстояние от центра окружности до середины стороны AB ровно 6 см .
Вычислите периметр трапецыи , веонинами которой является точка B , C , центр окружности и середина AB.
Видео:Геометрия. Задача. Четырёхугольник. Окружность.Скачать

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке N лежащей на стороне CD докажите что N середина CD?
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке N лежащей на стороне CD докажите что N середина CD.
Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
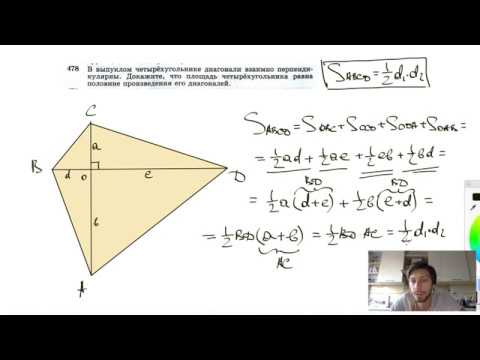
Биссектрисы углов А и В параллелограмма АВСD пересекаются в точке N лежащей на стороне CD докажите что N середина CD?
Биссектрисы углов А и В параллелограмма АВСD пересекаются в точке N лежащей на стороне CD докажите что N середина CD.
Видео:№43. Докажите, что середины сторон пространственного четырехугольника* являютсяСкачать

Угл А = углуВ = 90градусов точка О — середина АВ докажите что точка О — середина СД?
Угл А = углуВ = 90градусов точка О — середина АВ докажите что точка О — середина СД.
Видео:Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

В прямоугольнике ABCD точка M — середина BC?
В прямоугольнике ABCD точка M — середина BC.
Докажите, что треугольник AMD равнобедренный.
Видео:В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

ABCD — параллелограмм, точки M и K — середины сторон AB и BC соответственно (задание во вложении)?
ABCD — параллелограмм, точки M и K — середины сторон AB и BC соответственно (задание во вложении).
Если вам необходимо получить ответ на вопрос В выпуклом четырёхугольнике ABCD точка K — середина AB, точка L — середина BC, точка M — середина CD, точка N — середина DA?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
По поводу третьей задачи. В условии явная ошибка. 2 — мя лучами угол нельзя разделить на 4 равных угла, только на 3 угла по 40 градусов. При этом невозможно получить суммированием ни одного угла по 60 градусов. Разделить на 4 равных угла можно то..
Если сторона треугольника, вписанного в окружность, совпадает с диаметром (проходит через центр окружности), то это значит, что треугольник прямоугольный. Из этого делаем вывод, что треугольник АВС — прямоугольный, а угол В — прямой. Исходя из этог..
Тк АС — диаметр = > угол В 90 градусов угол С = 180 — 90 — 81 = 9 градусов.
Угол EBC = BEA (как накрестлежащие) угол BAE = 180 — ABE — BEA = 180 — 62 — 62 = 56 (по правилу треугольника) BAE = BCD = 56 (по правилу параллелограмма) ABC = ABE + EBC = 62 + 62 = 124 ADC = ABC = 124 ОТВЕТ : BAE = ADC = 56, ABC = ADC = 124.
Х — первый угол, тогда х + 20 второй угол х + х + 20 = 180(сумма смежных углов 180) 2х = 160 х = 80 — первый угол 80 + 20 = 100 — второй угол.
Нарисуем трапецию и проведём высоте BM. Площадь трапеции равна полусумму оснований на высоту, а средняя линия трапеции равна полусумме оснований. Зная площадь трапеции и среднюю линию, найдём высоту. 180 : 45 = 4 Далее AM² = AB² — BM² = 25 — 16 = ..
1) Площадь поверхности шара (сферы) можно найти по формуле : Sсф = 4πR². 2) Для того, чтобы найти радиус шара, рассмотрим ΔОВА — прямоугольный, ОВ = 4 см, АВ = 3 см, по т. Пифагора ОА = R = √(ОВ² + АВ²) = = √(4² + 3²) = √(16 + 9) = √25 = 5 (см). 3..
АМ = МВ = 16 / 2 = 8 см МК = КВ = 8 / 2 = 4 см АК = АМ + МК = 8 + 4 = 12 см Ответ : 12 см.
С) т. К. у ромба перпендикулярные диагонали, а не у прямоугольника.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°
Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Ваш ответ
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
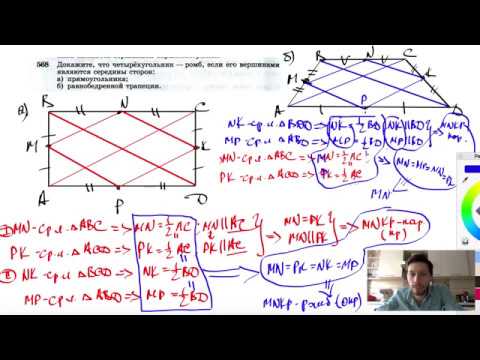
решение вопроса
Видео:№785. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD.Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,667
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
📽️ Видео
Геометрия В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNMСкачать

На стороне BC прямоугольника ABCD, у которого ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

11 класс, 43 урок, Вписанный четырехугольникСкачать

Все типы четырёхугольников в задании №12 ЕГЭ по базовой математике + профильСкачать















