V вектор s вектор t физика

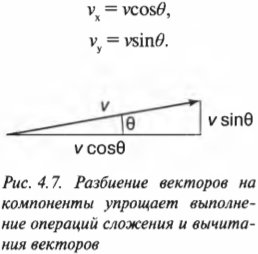
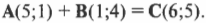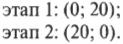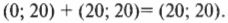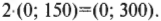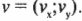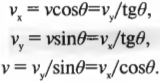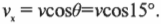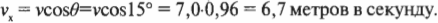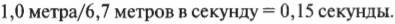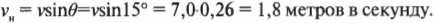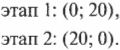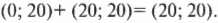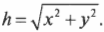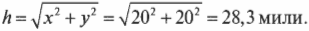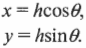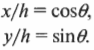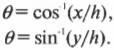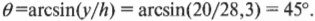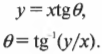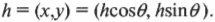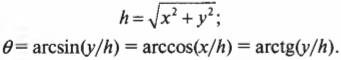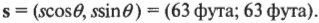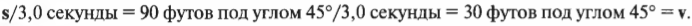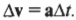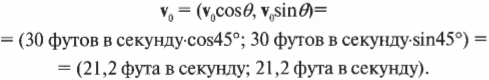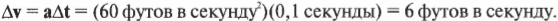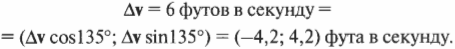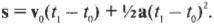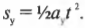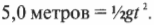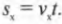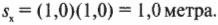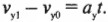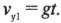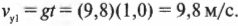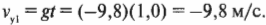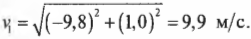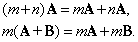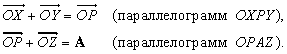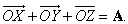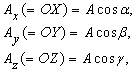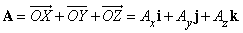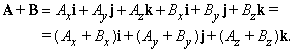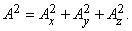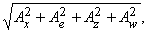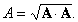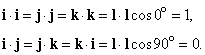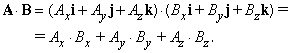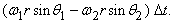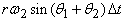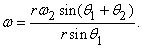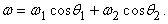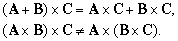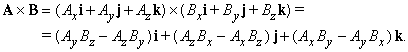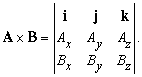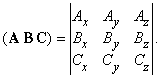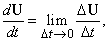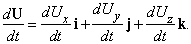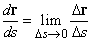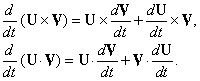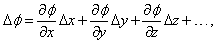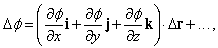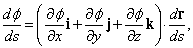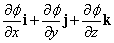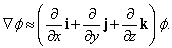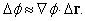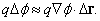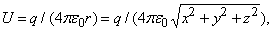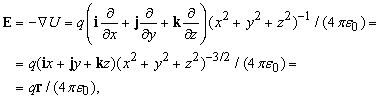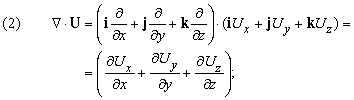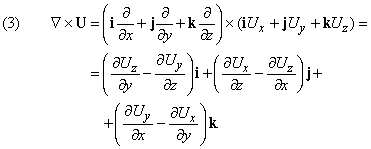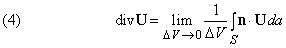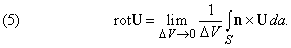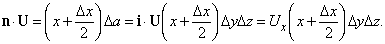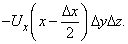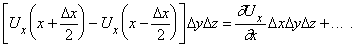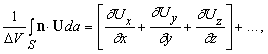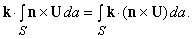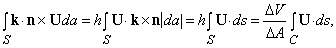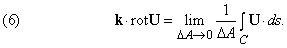• Изучаем сложение и вычитание векторов
• Выражаем векторы через координаты
• Разбиваем векторы на компоненты
• Выражаем перемещение, ускорение и скорость в виде векторов
• Определяем изменение скорости под действием тяготения

Довольно трудно добраться в место назначения — пешком ли, на велосипеде ли, на автомобиле ли, на самолете ли — если вы не знаете направления движения. Для успеха путешествия нужно знать не только расстояние, но и направление движения. В главе 3 описывались такие понятия, как перемещение, скорость и ускорение, связанные некоторыми соотношениями, как, например, ​ ( s=^1!/!_2at^2+v_0t ) ​. С помощью таких соотношений можно получить значения для ускорения, например 27 метров в секунду в квадрате, или для скорости, например 42,7 мили в час. Конечно, полезно знать эти параметры движения, но что можно сказать о направлении движения?

В реальном мире просто необходимо знать направление движения. Именно векторы обозначают такое направление. Очень многие люди ошибочно считают векторы очень сложными объектами, но это совсем не так. В этой главе вы узнаете, насколько легко и просто можно обращаться с ними при решении задач.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Осваиваем векторы

В главе 3 мы работали с простыми числами или измерениями, которые в физике называются величинами. Например, в результате измерения перемещения на 3 метра получена величина перемещения 3 метра. Вектор отличается от величины еще и наличием направления. В повседневной жизни на вопрос о пути понятие “вектор” возникает в виде следующего ответа встречного человека: “Это в 15 милях отсюда”. При этом величина вектора равна 15 милям, а направление вектора определяется взмахом руки. Когда вы навешиваете дверь на петли, то порой слышите совет: “Толкните сильнее влево”. Вот вам еще один вектор! Когда вы объезжаете препятствие на дороге, вам приходится ускоряться и замедляться в разных направлениях. Вот еще несколько векторов!

Векторы встречаются в обыденных ситуациях, например в дорожных указателях, инструкциях по сборке или даже при попытке избежать столкновения со встречным. Поскольку физика стоит за всеми событиями повседневной жизни, то не удивительно, что многие физические концепции, например скорость, ускорение, сила, являются векторами. По этой причине следует поближе познакомиться с векторами, поскольку они присутствуют во всех разделах физики. Вектор — это фундаментальное понятие физики.

Определяем направление: основные свойства векторов

При работе с векторами нужно иметь в виду его направление и величину. Физический параметр без направления, а только с величиной называется скаляром. Если к скаляру добавить направление, то получим вектор.

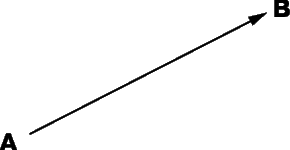
Визуально в физических задачах вектор отображается в виде стрелки. Действительно, стрелка имеет величину (т.е. длину) и направление (т.е. острие). Взгляните на рис. 4.1. Эта стрелка и есть вектор с началом в тупом конце и с окончанием — в заостренном конце.

Векторы можно использовать для представления силы, ускорения, скорости и других физических параметров. В физике для обозначения векторов используют полужирное начертание, например A. В некоторых книгах векторы обозначают стрелкой над символом, например ​ ( overrightarrow ) ​ . Стрелка обозначает, что у данного параметра ​A​, помимо величины, есть также направление.

Допустим, какой-то умник предложит вам дать пример вектора. Проще простого! Достаточно сказать, что у некого вектора А есть некая величина и некоторое направление. Убежден, что это произведет на умника оглушительное впечатление! Например, скажите, что вектор А направлен под углом 15° к горизонтали и имеет величину 12 метров в секунду. Итак, любопытный умник получит исчерпывающую информацию о векторе А.

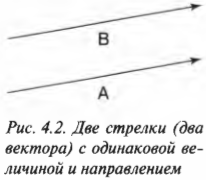
На рис. 4.2 показаны два вектора, А и В. Они очень похожи, поскольку обладают одинаковой длиной и направлением. Фактически оба эти вектора равны. Если два вектора равны по величине и направлению, то они считаются равными, т.е. А = В.

Очень скоро читатель станет настоящим экспертом в области векторов. Уже сейчас нам известно, что, когда мы встречаемся с символом А, это значит, что данный параметр обладает величиной и направлением, т.е. является вектором, а два вектора считаются равными, если они имеют одинаковую величину и направление. Но это еще далеко не все. Допустим, чтобы найти нужный вам отель, нужно проехать 20 миль к северу, а потом 20 миль на восток. Так насколько далеко и в каком направлении находится этот отель?

Комбинируем направления: сложение векторов

Два вектора можно сложить и получить результирующий вектор, который является суммой обоих векторов и определяет расстояние и направление до цели.

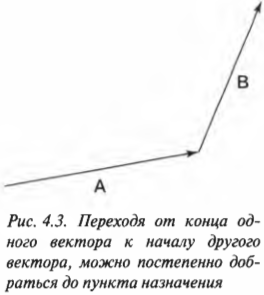
Допустим, что прохожий говорит вам, что для достижения пункта назначения вам нужно сначала следовать вектору А, а потом вектору В. Так где же находится в этом случае ваш пункт назначения? Сначала нужно проехать по пути, указанному вектором А, а потом по пути, указанному вектором В, как показано на рис. 4.3.

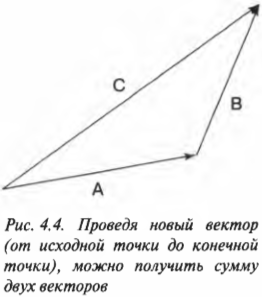
Когда вы доберетесь до конца вектора В, насколько далеко вы будете находиться от исходной точки? Для ответа на этот вопрос начертим еще один вектор С от исходной точки и до конечной точки путешествия, как показано на рис. 4.4.

Новый вектор С представляет собой результат всего путешествия от начала и до самого конца. Все, что нужно сделать, чтобы получить его, так это начертить оба вектора А и В и соединить новым результирующим вектором С.

Сумма векторов достигается за счет того, что начало одного вектора помещается в конец другого, т.е. суммарный вектор проходит от начала одного до конца другого вектора. Иначе говоря, С = А + В. При этом С называется суммой векторов, результатом сложения векторов, или результирующим вектором. Не думайте, что этим ограничиваются возможности комбинирования векторов, ведь векторы можно и вычитать.

Вычисляем разницу расстояний: разность векторов

А что если некто предложит вам векторы С и А, показанные на рис. 4.4, и попросит найти их разность? Их разностью является вектор В, поскольку при сложении векторов А и В получается вектор С. Чтобы объяснить эту мысль, нужно прояснить смысл вычитания вектора А из вектора С: т.е. смысл операции С — А.

Для вычитания двух векторов нужно расположить вместе основания векторов (т.е. концы векторов без остриев), а не совмещать основание одного вектора и острие другого вектора, как при сложении векторов. Затем нужно провести результирующий вектор, который является разностью двух векторов, от острия вычитающего вектора (А) к острию вычитаемого вектора (С). На рис. 4.5 показан пример вычитания вектора А из вектора С (иначе говоря, приведен пример С — А). Как видите, результат такого вычитания равен вектору В, поскольку С = А + В.

Еще один (и для некоторых более простой) способ вычитания векторов заключается в обращении направления второго вектора (т.е. вектора А в разности С — А) и сложении двух векторов: вектора С и обращенного вектора А (т.е. совмещении острия обращенного вектора А с основанием вектора С с последующим проведением результирующего вектора от основания обращенного вектора А к острию вектора С).

Как видите, сложение и вычитание векторов может происходить с одними и теми же векторами в одной задаче. На самом деле с векторами можно выполнять и некоторые другие математические операции. Изложенный выше материал означает, что с векторами можно оперировать так же, как со скалярами, например С = А + В, С — А = В и т.д. Как видите, векторы очень похожи на числа.

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Облекаем векторы в числа

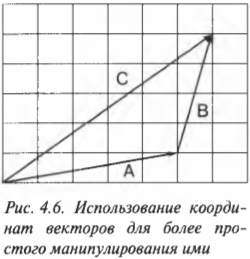
Векторы удобно представлять в виде стрелок, но это не всегда самый точный способ работы с ними. Векторы гораздо точнее можно характеризовать числами. Рассмотрим пример сложения векторов А + В, показанных на рис. 4.6.

Предположим, что измерения на рис. 4.6 даны в метрах. Это значит, что вектор А направлен на 1 метр вверх и на 5 метров вправо, а вектор В направлен на 1 метр вправо и на 4 метра вверх. Для получения параметров результирующего вектора С нужно сложить горизонтальные измерения обоих векторов и отдельно сложить вертикальные измерения обоих векторов.

Результирующий вектор С направлен на 6 метров вправо и на 5 метров вверх. Как видите, для получения вертикального измерения вектора С нужно сложить вертикальное измерение вектора А и вертикальное измерение вектора В. А для получения горизонтального измерения вектора С нужно сложить горизонтальное измерение вектора А и горизонтальное измерение вектора В.

Если процедура сложения векторов все еще очень туманна для вас, то тогда можно использовать другую систему обозначений векторов. Поскольку вектор А “простирается” на 5 метров вправо (в положительном направлении оси X) и на 1 метр вверх (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например А = (5;1). Аналогично, поскольку вектор В “простирается” на 1 метр вверх (в положительном направлении оси X) и на 4 метра вправо (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например В = (1;4).

С помощью такой системы обозначений сложение векторов существенно упрощается. Итак, для сложения двух векторов достаточно сложить их координаты по осям X и Y, чтобы получить координаты результирующего вектора по осям X и Y:

Получается, что весь секрет сложения векторов заключается в разбиении каждого вектора на координаты по осям X и Y с последующим их сложением, чтобы соответственно получить координаты X и Y результирующего вектора? Конечно, работа с этими числами для получения координат X и Y результирующего вектора требует некоторых усилий, но они достаточно просты, чтобы с успехом их выполнить.

Допустим, что нужный вам отель находится на расстоянии 20 миль к северу и на расстоянии 20 миль на восток. Как будет выглядеть вектор, направленный из исходной точки к этому отелю? С помощью координатного представления эта задача решается очень легко. Допустим, что положительное направление оси X направлено на восток, а положительное направление оси Y — на север. На первом этапе нужно проехать 20 миль на север, а на втором этапе — 20 миль на восток. В векторном представлении эта задача формулируется следующим образом (восток [X]; север [Y]):

Чтобы сложить эти два вектора, нужно сложить их координаты по соответствующим осям:

Результирующий вектор, который указывает на отель, имеет вид (20; 20).

Рассмотрим еще один пример удачного применения такого представления векторов. Допустим, что вы едете на гоночном автомобиле со скоростью 150 миль в час на восток и видите в зеркало заднего вида приближающегося соперника. Нет проблем, нужно лишь удвоить скорость:

Теперь вы уже не едете, а почти “летите” со скоростью 300 миль в час, но в том же направлении. Итак, в этой задаче демонстрируется процедура умножения вектора на скаляр.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Разбиение вектора на компоненты

Формулировки задач по физике с использованием векторов не всегда так просты, как предыдущие примеры с манипуляциями векторов. Рассмотрим первый вектор на рис. 4.1 с координатами (4; 1) и сравним его со следующей типичной формулировкой физической задачи: найти время перемещения шара со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. С помощью дальнейшей информации в этом разделе вы научитесь находить компоненты векторов и легко и просто манипулировать ими.

Ищем компоненты вектора по заданной величине и углу

Чтобы определить координаты вектора, нужно научиться разбивать векторы на части, которые называются компонентами. Например для вектора (4; 1) Х-компонентой является число 4, а Y-компонентой — число 1.

Часто в физической задаче задается угол и величина вектора, а его компоненты нужно определить. В предыдущем примере известно, что шар катится со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. Для определения времени перемещения шара от одного конца плоскости к другому нам потребуется разобраться только с Х-компонентой. То есть, задача сводится к определению времени перемещения на расстояние 1 метр вдоль оси X. Для ответа на этот вопрос нужно определить скорость перемещения шара по оси X.

Итак, нам известно, что шар движется со скоростью 7 метров в секунду под углом 15° к горизонтали (т.е. положительного направления оси X). В данной формулировке скорость является вектором ​ ( mathbf ) ​ с величиной 7 метров в секунду и направлением 15° к горизонтали.

Теперь нам нужно определить Х-компоненту вектора скорости шара, чтобы определить скорость перемещения шара вдоль основания наклонной плоскости. Х-компонента скорости является скаляром (т.е. имеет только значение, а не значение, направление и точку приложения, как вектор) и обозначается как ​ ( v_x ) ​. Аналогично, Y-компонента скорости шара также является скаляром и обозначается как ​ ( v_y ) ​. Итак, вектор скорости можно выразить через его компоненты:

Именно так выражается разложение вектора на компоненты. Так чему же равны компонента ( v_x ) и компонента ( v_y ) ? Скорость имеет величину ​ ( v ) ​ (7 метров в секунду) и направление ​ ( theta ) ​ (угол 15° к горизонтали). Также нам известна длина основания наклонной плоскости (1,0 метр). На рис. 4.7 показана схема тригонометрических функций (о, Боже, только не это!), которые описывают направление вектора скорости и помогут нам определить его компоненты. Не стоит волноваться: тригонометрические соотношения не так уж и сложны, если известен угол ​ ( theta ) ​, показанный на рис. 4.7. Величина (или модуль) вектора ( mathbf ) равна ​ ( v ) ​ (иногда если вектор обозначается символом ​ ( v ) ​, то его модуль обозначают символом ​ ( overline ) ​), а его компоненты определяются с помощью рис. 4.7:

Рекомендуется хорошенько запомнить указанные выше выражения для компонент вектора, поскольку нам придется довольно часто встречаться с ними в курсе физики.

Теперь можно пойти немного дальше и попробовать связать отдельные стороны треугольника на рис. 4.7. Это можно легко сделать, если вспомнить соотношение для тангенса ( tg,theta=sintheta/costheta ) и воспользоваться соотношениями для компонент скорости:

Зная соотношение ​ ( v_x=vcostheta ) ​, можно найти величину Х-компоненты скорости шара ( v_x=vcostheta ) :

Подставляя числа, получим

Итак, теперь мы знаем, что горизонтальная скорость шара равна 6,7 метров в секунду. Поскольку длина основания наклонной плоскости равна 1,0 метра, то это расстояние шар преодолеет за время:

Таким образом, благодаря тому, что мы научились определять компоненту скорости, нам удалось легко найти решение все задачи: шару потребуется 0,15 секунды для перемещения вдоль наклонной плоскости. А чему равна Y-компонента скорости? Это можно очень легко определить, поступая аналогично:

Находим величину и направление вектора по его компонентам

Иногда требуется определить угол наклона вектора, если известны его компоненты. Например, предположим, что вы ищите отель, расположенный на 20 миль к северу и на 20 миль к востоку. Под каким углом нужно двигаться к нему и насколько далеко он находится? Условия этой задачи можно записать с помощью уже известных нам векторных обозначений (см. предыдущий раздел):

После сложения этих двух векторов получим следующий результат:

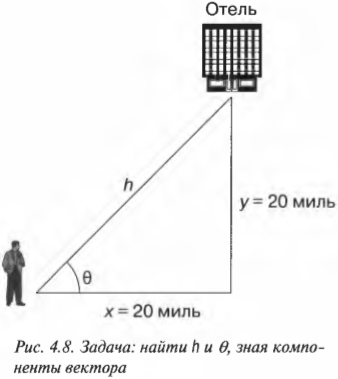
Результирующий вектор, который указывает на отель, имеет вид (20; 20). Это еще один способ указания вектора с помощью его компонент. Итак, вернемся к прежнему вопросу: под каким углом нужно двигаться к отелю и насколько далеко он находится от текущего положения? Иначе говоря, глядя на рис. 4.8, прежний вопрос теперь звучит так: “Чему равны ​ ( h ) ​ и ​ ( theta ) ​?”

Найти ​ ( h ) ​ не так уж и трудно, пользуясь теоремой Пифагора:

Подставляя численные значения, получим:

Итак, отель находится на расстоянии 28,3 мили. А под каким углом ​ ( theta ) ​ нужно ехать к нему по прямой? Пользуясь основными тригонометрическими соотношениями, можно записать:

Теперь для определения угла нужно использовать функции, обратные синусу и косинусу:

(Строго говоря, обратной синусу функцией является функция “арксинус”, или ​ ( arcsin(x) ) ​, а обратной косинусу — “арккосинус”, или ​ ( arccos(x) ) ​. Обозначения ​ ( sin^(x) ) ​ и ​ ( cos^(x) ) ​ часто используются для обозначения функций “арксинус” и “арккосинус”, но их не рекомендуется употреблять, чтобы не путать с функциями ​ ( 1/sin(x) ) ​ и ​ ( 1/cos(x) ) ​. — Примеч. ред.)

Как вычислить значения функций, обратных синусу (​ ( sin^ ) ​) и косинусу (​ ( cos^ ) ​)? Очень просто, ведь в любом инженерном калькуляторе есть кнопки для таких функций! (Например, в программе Калькулятор операционной системы Windows достаточно ввести число, установить флажок параметра Inv (Обратная) и щелкнуть на кнопке sin (Синус). — Примеч. ред.) Достаточно ввести число и нажать соответствующую кнопку, если таковая имеется, например с надписью arcsin (арксинус). В данном случае для угла ​ ( theta ) ​ получим следующий результат вычислений:

Итак, отель находится на расстоянии 28,3 мили и под углом 45°. Вот так, легко и просто мы успешно решили еще одну физическую задачу!

Аналогично, можно определить угол ( theta ) без необходимости промежуточного вычисления ​ ( h ) ​ с помощью других сведений из тригонометрии:

(Строго говоря, обратной тангенсу функцией является функция “арктангенс”, или ​ ( arctg(x) ) ​. Обозначение ​ ( tg^(x) ) ​ часто используется для обозначения функции “арктангенс”, но его не рекомендуется употреблять, чтобы не путать с функцией ​ ( 1/tg(x) ) ​. — Примеч. ред.)

Видео:Вектор в Физике. Как Рисовать Вектор? Модуль Вектора || Урок Физики 8 класс // Подготовка к ЕГЭСкачать

Срываем покров с векторов

У нас есть два способа описания векторов для решения физических задач. Первый основан на использовании компонент по осям X и Y, а второй — на величине (модуле) и направлении вектора (угол обычно задается в градусах от 0° до 360°, где угол 0° соответствует направлению вдоль положительного направления оси X). Знание правил взаимного преобразования этих двух способов описания имеет очень большое значение, поскольку для операций с векторами удобно использовать компоненты вектора, а в формулировке физических задач обычно задаются величины и углы векторов.

Вот как выглядит формула преобразования двух способов описания векторов:

В этом уравнении предполагается, что ​ ( theta ) ​ — это угол между горизонтальной компонентой и гипотенузой ​ ( h ) ​ (т.е. самой длинной стороной прямоугольного треугольника, расположенного напротив прямого угла), как показано на рис. 4.8. Если угол не известен, то его можно вывести, если запомнить, что сумма всех углов треугольника равна 180°, а в прямоугольном треугольнике, если вычесть величину прямого угла 90°, то сумма остальных двух углов равна 90°.

Если вам известны компоненты (х,у), то его величину и направление можно определить по следующим формулам:

Такого рода преобразования нужно уметь легко выполнять, поскольку они довольно часто встречаются в задачах. На этом месте часто многие приходят в растерянность и не могут освоить дальнейший материал именно потому, что не овладели простыми правилами разложения вектора на компоненты.

Перемещение — тоже вектор

Перемещение ​ ( s ) ​ следует обозначать ​ ( mathbf ) ​, как вектор с определенной величиной и направлением (для обозначения векторов иногда используют стрелку, которая располагается над именем переменной, например ​ ( overrightarrow ) ​ ). В реальном мире очень важно знать не только величину, но и направление перемещения.

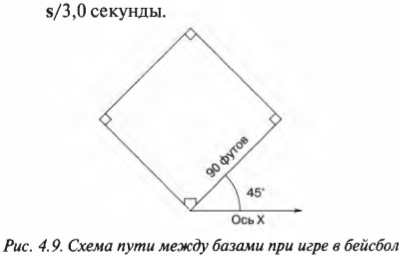
Допустим, что сбылись ваши детские мечты и вы стали звездой бейсбола. Вот вам нужно стремглав бежать к первой базе на расстоянии 90 футов по прямой. Но в каком направлении находится первая база? Допустим, что она находится под углом 45°, как показано на рис. 4.9. Тогда вектор вашего перемещения ( mathbf ) имеет величину 90 футов и направление 45°. А какими будут компоненты этого вектора? Это очень просто:

Скорость — еще один вектор

Представьте себе, что вы бежите к первой базе с вектором перемещения s с величиной 90 футов и направлением 45° по отношению к оси X. Тут стоило бы задаться вопросом: “Позволит мне моя скорость опередить игрока на первой базе?” Хороший вопрос. Достанем калькулятор и подсчитаем скорость, если известно, что для достижения первой базы вам требуется 3 секунды. Для определения скорости нужно поделить величину вектора ( mathbf ) на это время:

В этом выражении вектор перемещения делится на скаляр времени. Результатом такого деления является тоже вектор, а именно вектор скорости:

Итак, ваша скорость равна 30 футам в секунду под углом 45° и эта скорость является вектором ( mathbf ) . Деление вектора на скаляр дает вектор другой величины, но такого же направления. В данном примере деление вектора перемещения ( mathbf ) на скаляр времени дает в результате вектор ( mathbf ) . Он имеет такую же величину, что и величина перемещения, деленная на величину времени, но теперь вектор ( mathbf ) также имеет определенное направление, которое определяется направлением вектора перемещения ( mathbf ) . Итак, в данном примере мы научились манипулировать с векторами, как со скалярами в главе 3, и получать вектор в результате этих манипуляций.

Допустим, что после этих вычислений вы пришли к выводу, что такой скорости недостаточно, чтобы опередить соперника. Ну что ж, нужно срочно изменить направление!

Ускорение — еще один вектор

Что произойдет, если в процессе движения внезапно изменить направление? Вы сразу же почувствуете изменение скорости, а значит, ощутите ускорение. Как и скорость, ускорение ( mathbf ) является вектором.

Предположим, что в предыдущем примере нужно изменить скорость Y-компоненты скорости до величины 25 футов в секунду, чтобы избежать встречи с соперником, причем вам известно, что вы способны отклониться от курса на 90° с ускорением 60 футов в секунду в квадрате (в отчаянной попытке увильнуть от соперника). Достаточно ли этого ускорения для изменения скорости за ту долю секунды, которая отделяет вас от встречи с соперником?

Разница конечного ​ ( t_1 ) ​ и начального ​ ( t_0 ) ​ момента времени равняется изменению времени ​ ( Delta t ) ​. Теперь изменение скорости легко найти по следующей формуле:

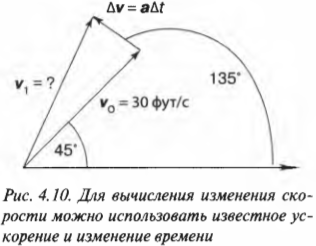
Теперь попробуем вычислить изменение скорости от исходной скорости на основе данных на рис. 4.10.

Для поиска конечного значения скорости ( mathbf ) нужно выполнить операцию сложения векторов. Это значит, что нужно разложить на компоненты вектор исходной скорости ​ ( mathbf ) ​ и вектор изменения скорости ​ ( Delta v ) ​. Вот как выглядят компоненты исходной скорости ​ ( mathbf ) ​:

Но что можно сказать о направлении ( Delta!mathbf ) ? Если взглянуть на рис. 4.10, то можно увидеть, что изменение скорости ( Delta!mathbf ) направлено под углом 90° к текущему направлению движения, которое ориентировано под углом 45° к положительному направлению оси X. Следовательно, изменение скорости ( Delta!mathbf ) направлено под углом 135° к положительному направлению оси X. Теперь можно получить выражение для компонент вектора изменения скорости ( Delta!mathbf ) :

Теперь остается только выполнить сложение векторов для поиска конечной скорости:

Итак, получен результат ​ ( mathbf ) ​ = (17,0 фута в секунду; 25,4 фута в секунду). Y-компонента конечной скорости больше необходимой величины, которая равна 25,0 фута в секунду. После завершения этих вычислений можно спрятать калькулятор и смело выполнить запланированный вираж. Представьте себе, что к изумлению окружающих вам удалось уклониться от соперника и успешно достигнуть места назначения — первой базы (какой крутой поворот вам пришлось для этого выполнить!). Болельщики изумлены и приветствуют вас, а вы, небрежно касаясь кепки кончиками пальцев, отдаете им честь, зная, что все это стало возможным благодаря превосходному знанию физики. После затишья вы украдкой бросаете взгляд на вторую базу: а не закрепить ли успех и попробовать добежать до второй базы? Для этого снова придется достать калькулятор и определить компоненты векторов.

Именно так нужно работать с векторами разных физических параметров: перемещения, скорости и ускорения. Теперь, обладая такими знаниями, можно перевести скалярные уравнения из главы 3 в векторную форму, например, вот так:

Обратите внимание, что полный вектор перемещения — это комбинация перемещения с начальной скоростью и перемещения с постоянным ускорением.

Видео:Физика | Ликбез по векторамСкачать

Упражнение со скоростью: скользим по радуге

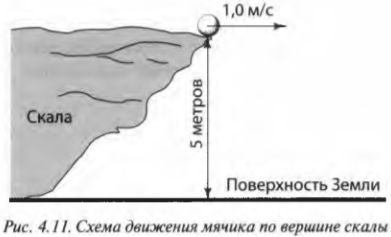
Хотя сила гравитации подробно описывается в главе 6, но здесь мы рассмотрим результат действия этой силы на небольшом примере с векторами в двух измерениях. Представьте себе, что мячик для игры в гольф движется по горизонтальной вершине скалы со скоростью 1,0 м/с и вскоре сорвется с края скалы на высоте 5 метров от поверхности Земли, как показано на рис. 4.11. Насколько далеко улетит мячик и с какой скоростью он столкнется с поверхностью Земли? В этой задаче прежде всего нужно определить время движения мячика.

Приступим к сбору фактов. Нам известно, что компоненты скорости мячика равны (1; 0), и он находится на высоте 5 метров от поверхности Земли. В процессе падения под действием силы тяготения Земли он движется с постоянным ускорением, ​ ( g ) ​, величина которого равна около 9,8 м/с 2 .

Итак, как определить, насколько далеко он упадет от края скалы? Один из способов решения этой задачи основан на определении времени движения мячика до столкновения с поверхностью Земли. Поскольку мячик ускоряется только в направлении оси Y (т.е. вертикально вниз), а его компонента скорости по оси X, ​ ( v_x ) ​, не меняется, то пройденное по горизонтали расстояние до столкновения будет равно ​ ( v_xt ) ​, где ​ ( t ) ​ — время движения мячика до столкновения. Сила тяготения ускоряет мячик по вертикали, а значит, перемещение по вертикали (т.е. вдоль оси Y) равно:

В данном случае перемещение по вертикали ​ ( s_y ) ​ = 5 метров, а ускорение ​ ( a_y ) ​ = ​ ( g ) ​ = 9,8 м/с 2 . Поэтому предыдущее уравнение принимает вид:

Это значит, что время движения мячика до столкновения равно:

Итак, мы вычислили, что мячик будет находиться в полете 1,0 секунды. Отлично, явный прогресс! Поскольку компонента скорости мячика по оси X не изменялась в течение этого времени, то можно легко вычислить расстояние, которое пролетит мячик по горизонтали (т.е. вдоль оси X) за это время:

Подставляем числа и получаем:

Итак, мячик столкнется с поверхностью Земли на расстоянии 1,0 метра по горизонтали.

Теперь можно приступать ко второму вопросу задачи: попробуем определить скорость мячика в момент столкновения с поверхностью Земли. Частично ответ на этот вопрос мы уже знаем, поскольку компонента скорости мячика по оси X не изменялась. Однако по вертикали сила тяготения ускорила мячик по вертикали (т.е. вдоль оси Y), а потому компоненты конечной скорости имеют следующий вид: (1,0; ?). Итак, нам нужно определить величину компоненты скорости мячика по оси Y, обозначенной вопросительным знаком. Воспользуемся следующим соотношением для компоненты скорости по вертикали:

В данном случае начальная скорость ​ ( v_ ) ​ = 0, постоянное ускорение ​ ( a_y=g ) ​ и нужно определить только конечную скорость ( v_ ) . Поэтому предыдущее уравнение приобретает следующий вид:

Подставляем числа и получаем:

Ускорение свободного падения, ​ ( g ) ​, также является вектором ​ ( mathbf ) ​. Он направлен к центру Земли, т.е. в отрицательном направлении оси Y, а на поверхности Земли его величина равна около -9,8 м/с 2 .

Отрицательный знак здесь обозначает направление вниз вектора ( mathbf ) , т.е. в отрицательном направлении оси Y. Итак, подставляем обновленное значение ускорения и получаем:

Итак, компоненты конечной скорости мячика равны (1,0; -9,8) м/с. Чтобы найти величину вектора скорости (а не его отдельных компонент) в момент столкновения с поверхностью Земли, выполним следующие вычисления:

Триумфальный финал! Мячик пролетит 1,0 метра по горизонтали и столкнется с поверхностью Земли со скоростью 9,9 м/с. Совсем неплохо для начала.

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Большая теория по векторам

И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь ((L)).

А некоторые имеют и число, и направление — например, перемещение ((vec)).

И сейчас ты узнаешь, почему это настолько важно.

Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Векторы — коротко о главном

Решать задачи с векторами — легко!

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Векторы и… Колумб

В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.

Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.

Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

О направлении

Направление – одна из важнейших характеристик движения.

Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.

Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.

Так вот, «просто числа» — это скалярные величины (их также называют скалярами).

А «числа с направлением» — это векторные величины (их иногда называют векторы).

В физике существует множество скалярных и векторных величин.

Видео:Физика. 9 класс. Векторы в механикеСкачать

Что такое скалярная величина?

Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)

Это, например, время, длина, масса, температура (продолжи сам!)

Видео:Введение в векторы и скаляры (видео 1)| Векторы. Прямолинейное движение | ФизикаСкачать

Что такое векторная величина?

Векторная величина – это величина, которая определяется и значением, и направлением.

В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.

Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Как обозначаются векторы?

Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: (vec)

Значение вектора – это модуль вектора, то есть его длина.

Обозначить это можно двумя способами: (left| <vec> right|) или (S)

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Операции над векторами

Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.

Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!

Умножение вектора на число

Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.

(Если направление противоположно, обозначаем так: (vecuparrow downarrow vec))

Рассмотрим на примере, используя клетку для точности построений:

Если вектор умножить на ноль, он станет нулевым.

Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:

Рассмотрим некоторые свойства нулевого вектора.

Если он нулевой, то его длина равна нулю! Логично, не правда ли?

А это значит, что его начало совпадает с концом, это просто какая-то точка.

Нулевой вектор – вектор, начало которого совпадает с концом.

Нулевой вектор принято считать сонаправленным любому вектору.

Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:

А если к любому вектору прибавит нулевой, ничего не изменится:

Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.

Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.

Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.

Две прямые параллельны: (qparallel p)

Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:

Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:

Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:

(vecuparrow downarrow vec)

Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.

Параллельный перенос векторов

Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.

Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство – параллельный перенос.

Сложение векторов по правилу треугольника

Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:

Наша цель – найти такой вектор, который будет являться суммой двух данных:

Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:

Теперь достроим до треугольника.

Но как узнать направление нужного нам вектора?

Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:

Это называется правилом треугольника.

Больше двух слагаемых векторов. Сложение по правилу многоугольника

Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?

Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:

Это называется правилом многоугольника.

Вычитание векторов через сложение

Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:

Тогда нам лишь остается найти сумму с обратным вектором:

А сделать это очень легко по правилу треугольника:

Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.

Вычитание векторов через треугольник

Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.

Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:

Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.

Универсальное правило параллелограмма

Есть еще один способ сложения и вычитания векторов.

Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.

Ничего не напоминает?

Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.

В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:

Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:

Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.

Скалярное произведение векторов

Еще одной важной операцией является произведение векторов. Рассмотрим скалярное произведение. Его результатом является скаляр.

Уравнение очень простое: произведение длин этих векторов на косинус угла между ними.

Векторное произведение векторов

Векторное произведение векторов пригодится нам в электродинамике.

Его формула лишь немного отличается от предыдущей:

В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!

После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:

Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.

Об этом мы поговорим подробнее, когда будем изучать электродинамику.

Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.

Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.

Видео:Радиус векторСкачать

Проекции векторов

Что такое проекция вектора и с чем ее едят?

Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.

Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.

Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.

Проекция вектора – словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.

Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.

Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.

Именно поэтому необходимо научиться работать с проекциями и осями.

Построение проекции. Определение знака

Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.

Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х₀) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.

Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, – большое заблуждение.

Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:

Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.

В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:

Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:

Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:

Рассмотрим еще один интересный случай.

Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!

Анализ углов

Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!

Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось. Получим угол между вектором и осью.

Если угол острый, проекция положительна:

Если угол тупой, проекция отрицательна:

Обрати особое внимание на то, какой именно угол является углом между вектором и осью!

Частные случаи проекции

Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.

Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180 О ). Это зависит от направления.

При этом длина проекции совпадает с длиной вектора! Смотри!

Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:

Если вектор направлен в другую сторону, проекция отрицательна:

Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.

Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.

Что? Почему раньше не сказал? А… Ну…

Хватит вопросов! Вот тебе пример:

(vec) направлен противоположно оси. Его проекция отрицательна.

Еще один частный случай – работа с обратными векторами.

Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:

Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.

Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.

Прямоугольные треугольники равны по углу и гипотенузе. Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:

Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:

Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.

Проекции обратных векторов равны по модулю и противоположны по знаку.

Давайте еще раз уточним.

Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).

Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.

Проекция вектора бывает отрицательной. Это зависит от направления вектора.

Способы нахождения проекций и векторов с помощью тригонометрии

Зная угол между вектором и осью, можно не прибегать к координатам. Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.

Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.

Рассмотрим вектор и его проекции на оси:

Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:

Тогда обозначим прямой угол и угол между вектором и осью:

Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.

Из этих уравнений легко выражаются проекции.

А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:

Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.

Видео:А ТЫ УЖЕ РАЗОБРАЛСЯ С УМНОЖЕНИЕМ ВЕКТОРОВ? ЧАСТЬ II #математика #егэ #огэ #формулы #профильныйегэСкачать

Действия над проекциями векторов. Решение задач

Умение применять свои знания на практике невероятно важны. Это касается не только физики.

Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.

Сложение проекций. Доказательство главного свойства

Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:

Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:

Давай посчитаем проекции векторов и проекцию вектора их суммы:

Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!

Намного важнее уметь доказывать гипотезы в общем виде.

Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!

Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:

Затем запишем, чему равна сумма этих векторов.

Мы доказали нашу гипотезу.

Но что насчет разности?

Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!

Проекция суммы векторов равна сумме проекций векторов.

Проекция разности векторов равна разности проекций векторов.

Или можно записать так:

Простейшие задачи на нахождение проекций

Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.

Давай научимся с ними работать.

Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.

Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.

В первом случае вектор направлен против оси Х.

Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.

Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!

Рассмотрим второй вектор.

Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.

Убедимся в этом.

На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:

Рассмотрим (vec). Заметим, что он является обратным для (vec): их длины равны, а направления противоположны.

Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:

Поступаем с (vec) так же, как поступали с первым вектором.

Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.

Проведя перпендикуляры, считаем проекцию на ось Y:

С (vec) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:

Задачи на нахождение вектора и его угла с осью

С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.

Давай попробуем это сделать.

Даны проекции вектора на две оси. Для начала нарисуем оси:

Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.

С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?

Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.

Проекция на ось Y положительна. Вектор смотрит в ту же сторону, что и ось.

Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:

Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:

Обозначим угол (alpha ), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?

Рассмотрим смежный ему угол (beta ). Его найти гораздо проще, а в сумме они дадут 180 градусов.

Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла (beta ) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.

Вычитанием угла (beta ) из 180 градусов найдем угол (alpha ):

Главный метод работы с осями и проекциями в решении физических задач

В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.

Поэтому важно научиться искать проекции вектора и связывать их с ней.

Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):

Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.

Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.

Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.

Сделаем это для данного рисунка:

Мы видим, что остальные векторы расположены к осям под каким-то углом.

Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:

Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:

Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.

Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:

Переходим к векторам, которые расположены под углом.

Выглядит страшно, но это не так!

Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.

Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).

Обозначим, что является проекцией. Это катет:

Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.

Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.

Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…

Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Видео:Векторы для чайников (что потребуется знать при решении физических задач)Скачать

Заключение

Итак, теперь мы знаем о векторах очень много! Мы выяснили, зачем они нужны и как с ними работать, а еще разобрали их роль в решении различных задач. Теперь векторы — наша прочная опора.

Именно из таких знаний складывается порой нечто более сложное и комплексное, что-то, что безусловно нам однажды поможет.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

ВЕКТОР

ВЕКТОР. В физике и математике вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами».

Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, мы хотим описать положение предмета относительно некоторой точки. Мы можем сказать, сколько километров от точки до предмета, но не можем полностью определить его местоположение, пока не узнаем направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.

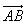
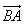
Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как на рис. 1. Например, для того чтобы представить графически силу в пять килограммов, надо нарисовать отрезок прямой длиной в пять единиц в направлении действия силы. Стрелка указывает, что сила действует от A к B; если бы сила действовала от B к A, то мы бы записали или . Для удобства векторы обычно обозначаются полужирными прописными буквами (A, B, C и так далее); векторы A и –A имеют равные численные значения, но противоположны по направлению. Численное значение вектора А называется модулем или длиной и обозначается A или |A|. Это величина, конечно, скаляр. Вектор, начало и конец которого совпадают, называется нулевым и обозначается O.

Два вектора называются равными (или свободными), если их модули и направления совпадают. В механике и физике этим определением, однако, надо пользоваться с осторожностью, так как две равных силы, приложенные к различным точкам тела в общем случае будут приводить к различным результатам. В связи с этим векторы подразделяются на «связанные» или «скользящие», следующим образом:

Связанные векторы имеют фиксированные точки приложения. Например, радиус-вектор указывает положение точки относительно некоторого фиксированного начала координат. Связанные векторы считаются равными, если у них совпадают не только модули и направления, но они имеют и общую точку приложения.

Скользящими векторами называются равные между собой векторы, расположенные на одной прямой.

Видео:Сложение векторов. 9 класс.Скачать

Сложение векторов.

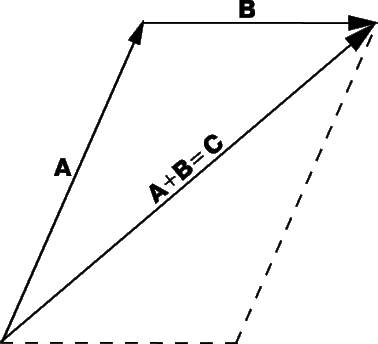
Идея сложения векторов возникла из того, что мы можем найти единственный вектор, который оказывает то же воздействие, что и два других вектора вместе. Если для того, чтобы попасть в некоторую точку, нам надо пройти сначала A километров в одном направлении и затем B километров в другом направлении, то мы могли бы достичь нашей конечной точки пройдя C километров в третьем направлении (рис. 2). В этом смысле можно сказать, что

Вектор C называется «результирующим вектором» A и B, он задается построением, показанным на рисунке; на векторах A и B как на сторонах построен параллелограмм, а C – диагональ, соединяющая начало А и конец В. Из рис. 2 видно, что сложение векторов «коммутативно», т.е.

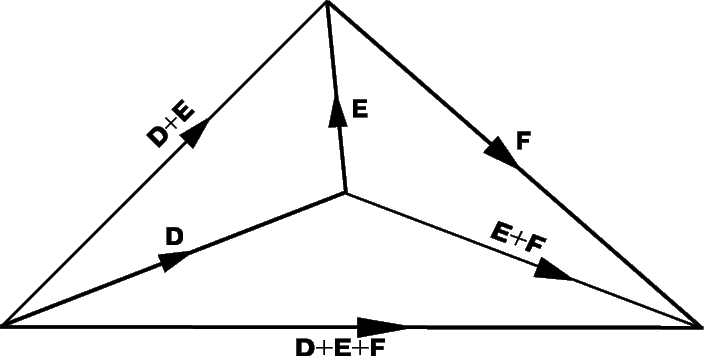
Аналогичным образом можно сложить несколько векторов, последовательно соединяя их «непрерывной цепочкой», как показано на рис. 3 для трех векторов D, E и F. Из рис. 3 также видно, что

т.е. сложение векторов ассоциативно. Суммировать можно любое число векторов, причем векторы необязательно должны лежать в одной плоскости. Вычитание векторов представляется как сложение с отрицательным вектором. Например,

где, как определялось ранее, –B – вектор, равный В по модулю, но противоположный по направлению.

Это правило сложения может теперь использоваться как реальный критерий проверки, является ли некоторая величина вектором или нет. Перемещения обычно подчиняются условиям этого правила; то же можно сказать и о скоростях; силы складываются таким же образом, как можно было видеть из «треугольника сил». Однако, некоторые величины, обладающие как численными значениями так и направлениями, не подчиняются этому правилу, поэтому не могут рассматриваться как векторы. Примером являются конечные вращения.

Видео:Построение проекции вектора на осьСкачать

Умножение вектора на скаляр.

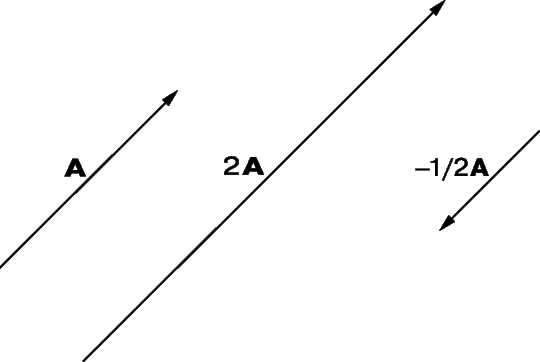
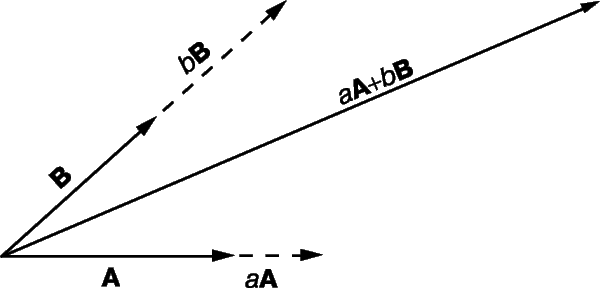
Произведение mA или Am, где m (m № 0) – скаляр, а A – ненулевой вектор, определяется как другой вектор, который в m раз длиннее A и имеет тоже направление что и A, если число m положительно, и противоположное, если m отрицательно, как показано на рис. 4, где m равно 2 и –1/2 соответственно. Кроме того, 1A = A, т.е. при умножении на 1 вектор не изменяется. Величина –1A – вектор, равный A по длине, но противоположный по направлению, обычно записывается как –A. Если А – нулевой вектор и(или) m = 0, то mA – нулевой вектор. Умножение дистрибутивно, т.е.

Мы можем складывать любое число векторов, причем порядок слагаемых не влияет на результат. Верно и обратное: любой вектор раскладывается на две или более «компоненты», т.е. на два вектора или более, которые, будучи сложенными, в качестве результирующего дадут исходный вектор. Например, на рис. 2, A и B – компоненты C.

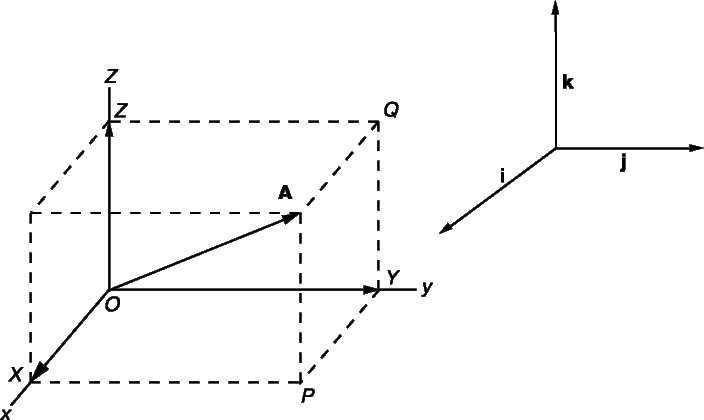
Многие математические действия с векторами упрощаются, если разложить вектор на три компоненты по трем взаимно перпендикулярным направлениям. Выберем правую систему декартовых координат с осями Ox, Oy и Oz как показано на рис. 5. Под правой системой координат мы подразумеваем, что оси x, y и z располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки. Из одной правой системы координат всегда можно получить другую правую систему координат соответствующим вращением. На рис. 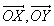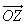5, показано разложение вектор A на три компоненты и . Они в сумме составляют вектор A, так как

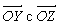
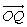
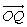
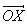
Можно было бы также сначала сложить и получить , а затем к прибавить .

Проекции вектора А на три координатные оси, обозначенные A_x, A_y и A_z называются «скалярными компонентами» вектора A:

где a , b и g – углы между A и тремя координатными осями. Теперь введем три вектора единичной длины i, j и k (орты), имеющие то же самое направление, что и соответствующие оси x, y и z. Тогда, если A_x умножить на i, то полученное произведение – это вектор, равный 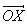, и

Два вектора равны тогда и только тогда, когда равны их соответствующие скалярные компоненты. Таким образом, A = B тогда и только тогда, когда A_x = B_x, A_y = B_y, A_z = B_z.

Два вектора можно сложить, складывая их компоненты:

Кроме того, по теореме Пифагора:

Видео:Лекция 5. Сложение и вычитание векторов │ФИЗИКА С НУЛЯ теорияСкачать

Линейные функции.

Выражение aA + bB, где a и b – скаляры, называется линейной функцией векторов A и B. Это вектор, находящийся в той же плоскости, что A и B; если A и B не параллельны, то при изменении a и b вектор aA + bB будет перемещаться по всей плоскости (рис. 6). Если A, B и C не все лежат в одной плоскости, то вектор aA + bB + cC (a, b и c изменяются) перемещается по всему пространству. Предположим, что A, B и C – единичные векторы i, j и k. Вектор ai лежит на оси x; вектор ai + bj может перемещаться по всей плоскости xy; вектор ai + bj + ck может перемещаться по всему пространству.

Можно было бы выбрать четыре взаимно перпендикулярных вектора i, j, k и l и определить четырехмерный вектор как величину

а можно было бы продолжать до пяти, шести или любого числа измерений. Хотя визуально такой вектор представить невозможно, никаких математических трудностей здесь не возникает. Такая запись часто бывает полезна; например, состояние движущейся частицы описывается шестимерным вектором P (x, y, z, p_x, p_y, p_z), компоненты которого – ее положение в пространстве (x, y, z) и импульс (p_x, p_y, p_z). Такое пространство называется «фазовым пространством»; если мы рассматриваем две частицы, то фазовое пространство 12-мерное, если три, то 18-ти и так далее. Число размерностей можно неограниченно увеличивать; при этом величины, с которыми мы будем иметь дело, ведут себя во многом также, как те, которые мы рассмотрим в оставшейся части этой статьи, а именно, трехмерные векторы.

Умножение двух векторов.

Правило сложения векторов было получено путем изучения поведения величин, представленных векторами. Нет никаких видимых причин, по которым два вектора нельзя было бы каким-либо образом перемножить, однако это умножение будет иметь смысл только в том случае, если можно показать его математическую состоятельность; кроме того, желательно, чтобы произведение имело определенный физический смысл.

Существуют два способа умножения векторов, которые соответствуют этим условиям. Результатом одного из них является скаляр, такое произведение называется «скалярным произведением» или «внутренним произведением» двух векторов и записывается A Ч B или (A, B). Результатом другого умножения является вектор, называемый «векторным произведением» или «внешним произведением» и записывается A ґ B или [A, B]. Скалярные произведения имеют физический смысл для одного-, двух- или трех измерений, тогда как векторные произведения определены только для трех измерений.

Скалярные произведения.

Если под действием некоторой силы F точка, к которой она приложена, перемещается на расстояние r, то выполненная работа равна произведению r и компоненты F в направлении r. Эта компонента равна F cos б F, r с , где б F, r с – угол между F и r, т.е.

Произведенная работа = Fr cos б F, r с .

Это – пример физического обоснования скалярного произведения, определенного для любых двух векторов A, B посредством формулы

Так как все величины правой части уравнения – скаляры, то

следовательно, скалярное умножение коммутативно.

Скалярное умножение также обладает свойством дистрибутивности:

Если векторы A и B перпендикулярны, то cos б A, B с равен нулю, и, поэтому, A Ч B = 0, даже если ни A, ни B не равны нулю. Именно поэтому мы не можем делить на вектор. Допустим, что мы разделили обе части уравнения A Ч B = A Ч C на A. Это дало бы B = C, и, если бы можно было бы выполнить деление, то это равенство стало бы единственным возможным результатом. Однако, если мы перепишем уравнение A Ч B = A Ч C в виде A Ч (B – C) = 0 и вспомним, что (B – C) – вектор, то ясно, что (B – C) необязательно равен нулю и, следовательно, B не должен быть равным C. Эти противоречивые результаты показывают, что векторное деление невозможно.

Скалярное произведение дает еще один способ записи численного значения (модуля) вектора:

Скалярное произведение можно записать и другим способом. Для этого вспомним, что:

Поскольку последнее уравнение содержит x, y и z в качестве нижних индексов, уравнение, казалось бы, зависит от выбранной конкретной системы координат. Однако это не так, что видно из определения, которое не зависит от выбранных координатных осей.

Векторные произведения.

Векторным или внешним произведением векторов называется вектор, модуль которого равен произведению их модулей на синус угла, перпендикулярный исходным векторам и составляющий вместе с ними правую тройку. Это произведение легче всего ввести, рассматривая соотношение между скоростью и угловой скоростью. Первая – вектор; мы теперь покажем, что последнюю также можно интерпретировать как вектор.

Угловая скорость вращающегося тела определяется следующим образом: выберем любую точку на теле и проведем перпендикуляр из этой точки до оси вращения. Тогда угловая скорость тела – это число радиан, на которые эта линия повернулась за единицу времени.

Если угловая скорость – вектор, она должна иметь численное значение и направление. Численное значение выражается в радианах в секунду, направление можно выбрать вдоль оси вращения, можно его определить, направив вектор в том направлении, в котором двигался бы правосторонний винт при вращении вместе с телом.

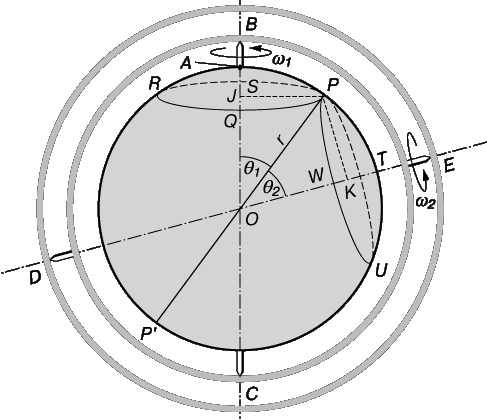
Рассмотрим вращение тела вокруг фиксированной оси. Если установить эту ось внутри кольца, которое в свою очередь закреплено на оси, вставленной внутрь другого кольца, мы можем придать вращение телу внутри первого кольца с угловой скоростью w 1 и затем заставить внутреннее кольцо (и тело) вращаться с угловой скоростью w 2. Рисунок 7 поясняет суть дела; круговые стрелки показывают направления вращения. Данное тело – это твердая сфера с центром О и радиусом r.

Придадим этому телу движение, которое является суммой двух различных угловых скоростей. Это движение довольно трудно представить наглядно, но достаточно очевидно, что тело больше не вращается относительно фиксированной оси. Однако все-таки можно сказать, что оно вращается. Чтобы показать это, выберем некоторую точку P на поверхности тела, которая в рассматриваемый нами момент времени находится на большом круге, соединяющем точки, в которых две оси пересекают поверхность сферы. Опустим перпендикуляры из P на оси. Эти перпендикуляры станут радиусами PJ и PK окружностей PQRS и PTUW соответственно. Проведем прямую POP ў , проходящую через центр сферы. Теперь точка P, в рассматриваемый момент времени одновременно перемещается по окружностям, которые соприкасаются в точке P. За малый интервал времени D t, P перемещается на расстояние

Это расстояние равно нулю, если

В этом случае точка P находится в состоянии мгновенного покоя, и точно также все точки на прямой POP ў . Остальная часть сферы будет в движении (окружности, по которым перемещаются другие точки, не касаются, а пересекаются). POP ў является, таким образом, мгновенной осью вращения сферы, подобно тому, как колесо, катящееся по дороге в каждый момент времени, вращается относительно своей нижней точки.

Чему равна угловая скорость сферы? Выберем для простоты точку A, в которой ось w 1 пересекает поверхность. В момент времени, который мы рассматриваем, она перемещается за время D t на расстояние

по кругу радиуса r sin w 1. По определению, угловая скорость

Из этой формулы и соотношения (1) мы получим

Другими словами, если записать численное значение и выбрать направление угловой скорости так, как это описано выше, то эти величины складываются как векторы и могут быть рассмотрены как таковые.

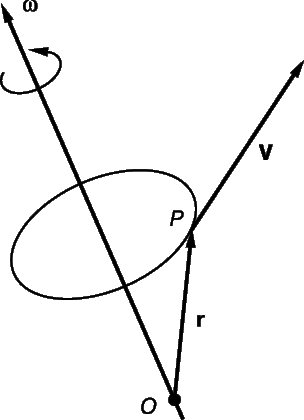
Теперь можно ввести векторное произведение; рассмотрим тело, вращающееся с угловой скоростью w . Выберем любую точку P на теле и любое начало координат О, которое находится на оси вращения. Пусть r – вектор, направленный от О к P. Точка P движется по окружности со скоростью

Вектор скорости V является касательным к окружности и указывает в направлении, показанном на рис. 8.

Это уравнение дает зависимость скорости V точки от комбинации двух векторов w и r. Используем это соотношение, чтобы определить новый вид произведения, и запишем:

Так как результатом такого умножения является вектор, это произведение названо векторным. Для любых двух векторов A и B, если

и направление вектора C таково, что он перпендикулярен плоскости, проходящей через А и B и указывает в направлении, совпадающем с направлением движения правовращающегося винта, если он параллелен C и вращается от A к B. Другими словами, мы можем сказать, что A, B и C, расположенные в таком порядке, образуют правый набор координатных осей. Векторное произведение антикоммутативно; вектор B ґ A имеет тот же модуль, что и A ґ B, но направлен в противоположную сторону:

Это произведение дистрибутивно, но не ассоциативно; можно доказать, что

Посмотрим, как записывается векторное произведение в терминах компонент и единичных векторов. Прежде всего, для любого вектора A,

Следовательно, в случае единичных векторов,

Это равенство также можно записать в виде определителя:

Если A ґ B = 0, то либо A или B равно 0, либо A и B коллинеарны. Таким образом, как и в случае скалярного произведения, деление на вектор невозможно. Величина A ґ B равна площади параллелограмма со сторонами A и B. Это легко видеть, так как B sin б A, B с – его высота и A – основание.

Существует много других физических величин, которые являются векторными произведениями. Одно из наиболее важных векторных произведений появляется в теории электромагнетизма и называется вектором Пойтинга P. Этот вектор задается следующим образом:

где E и H – векторы электрического и магнитного полей соответственно. Вектор P можно рассматривать как заданный поток энергии в ваттах на квадратный метр в любой точке. Приведем еще несколько примеров: момент силы F (крутящий момент) относительно начала координат, действующей на точку, радиус-вектор которой r, определяется как r ґ F; частица, находящаяся в точке r, массой m и скоростью V, имеет угловой момент mr ґ V относительно начала координат; сила, действующая на частицу, несущую электрический заряд q через магнитное поле B со скоростью V, есть qV ґ B.

Тройные произведения.

Из трех векторов мы можем сформировать следующие тройные произведения: вектор (A Ч B) ґ C; вектор (A ґ B) ґ C; скаляр (A ґ B) Ч C.

Первый тип – произведение вектора C и скаляра A Ч B; о таких произведениях мы уже говорили. Второй тип называется двойным векторным произведением; вектор A ґ B перпендикулярен к плоскости, где лежат A и B, и поэтому (A ґ B) ґ C – вектор, лежащий в плоскости A и B и перпендикулярный C. Следовательно, в общем случае, (A ґ B) ґ C № A ґ (B ґ C). Записав A, B и C через их координаты (компоненты) по осям x, y и z и умножив, можно показать, что A ґ (B ґ C) = B ґ (A Ч C) – C ґ (A Ч B). Третий тип произведения, который возникает при расчетах решетки в физике твердого тела, численно равен объему параллелепипеда с ребрами A, B, C. Так как (A ґ B) Ч C = A Ч (B ґ C), знаки скалярного и векторного умножений можно менять местами, и произведение часто записывается как (A B C). Это произведение равно определителю

Заметим, что (A B C) = 0, если все три вектора лежат в одной и той же плоскости или, если А = 0 или (и) В = 0 или (и) С = 0.

ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА

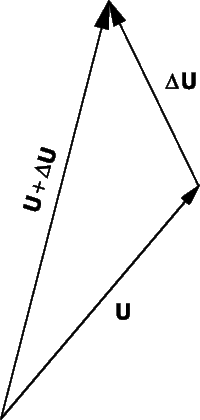
Предположим, что вектор U является функцией одной скалярной переменной t. Например, U может быть радиус-вектором, проведенным из начала координат до перемещающейся точки, а t – временем. Пусть t изменится на небольшую величину D t, что приведет к изменению U на величину D U. Это показано на рис. 9. Отношение D U/ D t – вектор, направленный в том же направлении, что и D U. Мы можем определить производную U по t, как

при условии, что такой предел существует. С другой стороны, можно представить U как сумму компонент по трем осям и записать

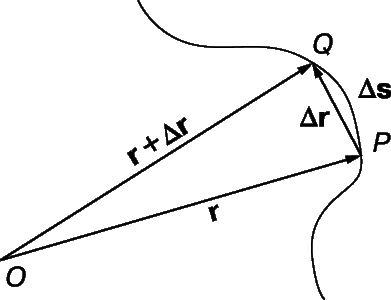
Если U – радиус-вектор r, то dr/dt – скорость точки, выраженная как функция времени. Продифференцировав по времени еще раз, мы получим ускорение. Предположим, что точка перемещается вдоль кривой, показанной на рис. 10. Пусть s – расстояние, пройденное точкой вдоль кривой. В течение малого интервала времени D t точка пройдет расстояние D s вдоль кривой; положение радиус-вектора изменится на D r. Следовательно D r/ D s – вектор направленный как D r. Далее

есть единичный вектор, касательный к кривой. Это видно из того, что при приближении точки Q к точке P, PQ приближается к касательной и D r приближается к D s.

Формулы для дифференцирования произведения подобны формулам для дифференцирования произведения скалярных функций; однако, так как векторное произведение антикоммутативно, порядок умножения должен быть сохранен. Поэтому,

Таким образом, мы видим, что, если вектор является функцией одной скалярной переменной, то мы можем представить производную почти также, как в случае скалярной функции.

Вектор и скалярные поля.

Градиент.

В физике часто приходится иметь дело с векторными или скалярными величинами, которые меняются от точки к точке в заданной области. Такие области называются «полями». Например, скаляр может быть температурой или давлением; вектор может быть скоростью движущейся жидкости или электростатическим полем системы зарядов. Если мы выбрали некоторую систему координат, то любой точке P (x, y, z) в заданной области соответствует некоторый радиус-вектор r (= xi + yj + zk) и также значение векторной величины U (r) или скаляра f (r), связанных с ним. Предположим, что U и f определены в области однозначно; т.е. каждой точке соответствует одна и только одна величина U или f , хотя различные точки могут, конечно, иметь различные значения. Допустим, что мы хотим описать скорость, с которой U и f изменяются при передвижении по этой области.

Простые частные производные, такие, как ¶ U/ ¶ x и ¶f / ¶ y, нас не устраивают, потому что они зависят от конкретно выбранных координатных осей. Однако можно ввести векторный дифференциальный оператор, независимый от выбора осей координат; этот оператор называется «градиентом».

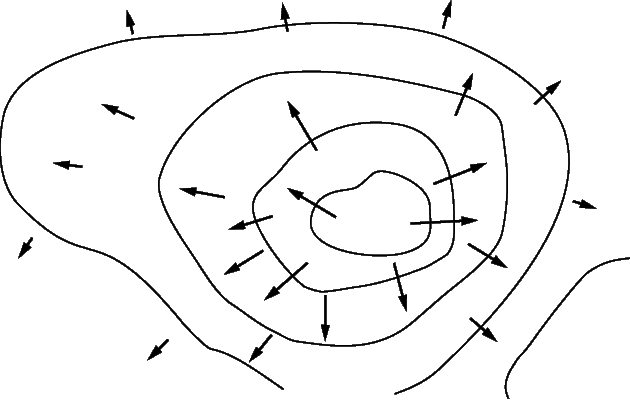
Пусть мы имеем дело со скалярным полем f . Сначала в качестве примера рассмотрим контурную карту области страны. В этом случае f – высота над уровнем моря; контурные линии соединяют точки с одним и тем же значением f . При движении вдоль любой из этих линий f не меняется; если двигаться перпендикулярно этим линиям, то скорость изменения f будет максимальной. Мы можем каждой точке сопоставить вектор, указывающий величину и направление максимального изменения скорости f ; такая карта и некоторые из этих векторов показаны на рис. 11. Если мы проделаем это для каждой точки поля, то получим векторное поле, связанное со скалярным полем f . Это поле вектора, называемого «градиентом» f , который записывается как grad f или Сf (символ С также называется «набла»).

В случае трех измерений, контурные линии становятся поверхностями. Малое смещение D r (= i D x + j D y + k D z) приводит к изменению f , которое записывается как

где точками обозначены члены более высоких порядков. Это выражение можно записать в виде скалярного произведения

Разделим правую и левую части этого равенства на D s, и пусть D s стремится к нулю; тогда

где dr/ds – единичный вектор в выбранном направлении. Выражение в круглых скобках – вектор, зависящий от выбранной точки. Таким образом, d f /ds имеет максимальное значение, когда dr/ds указывает в том же направлении, выражение, стоящее в скобках, является градиентом. Таким образом,

– вектор, равный по величине и совпадающий по направлению с максимальной скоростью изменения f относительно координат. Градиент f часто записывается в виде

Это означает, что оператор С существует сам по себе. Во многих случаях он ведет себя, как вектор, и фактически является «векторным дифференциальным оператором» – одним из наиболее важных дифференциальных операторов в физике. Несмотря на то, что С содержит единичные векторы i, j и k, его физический смысл не зависит от выбранной системы координат.

Какова связь между Сf и f ? Прежде всего предположим, что f определяет потенциал в любой точке. При любом малом смещении D r величина f изменится на

Если q – величина (например масса, заряд), перемещенная на D r, то работа, выполненная при перемещении q на D r равна

Так как D r – перемещение, то q Сf – сила; – Сf – напряженность (сила на единицу количества), связанная с f . Например, пусть U – электростатический потенциал; тогда E – напряженность электрического поля, задается формулой

Допустим, что U создается точечным электрическим зарядом в q кулонов, помещенным в начало координат. Значение U в точке P (x, y, z) с радиус-вектором r задается формулой

где e 0 – диэлектрическая постоянная свободного пространства. Поэтому

откуда следует, что E действует в направлении r и его величина равна q/(4 pe 0r 3 ).

Зная скалярное поле, можно определить связанное с ним векторное поле. Также возможно и обратное. С точки зрения математической обработки скалярными полями оперировать легче, чем векторными, так как они задаются одной функцией координат, в то время как векторное поле требует три функции, соответствующие компонентам вектора в трех направлениях. Таким образом, возникает вопрос: дано векторное поле, может ли мы записать связанное с ним скалярное поле?

Дивергенция и ротор.

Мы видели результат действия С на скалярную функцию. Что произойдет, если С применить к вектору? Имеются две возможности: пусть U (x, y, z) – вектор; тогда мы можем образовать векторное и скалярное произведения следующим образом:

Первое из этих выражений – скаляр, называемый дивергенцией U (обозначается divU); второе – вектор, названный ротор U (обозначается rotU).

Эти дифференциальные функции, дивергенция и ротор, широко используются в математической физике.

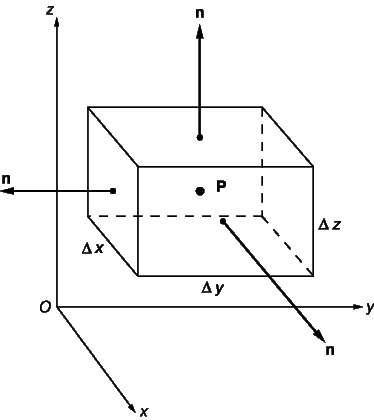
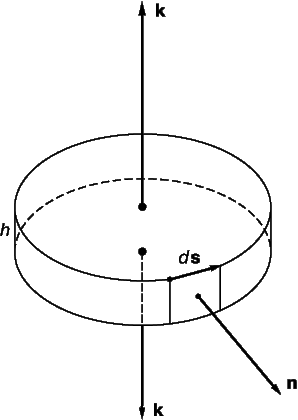
Представьте, что U – некоторый вектор и что он и его первые производные непрерывны в некоторой области. Пусть P – точка в этой области, окруженная малой замкнутой поверхностью S, ограничивающей объем D V. Пусть n – единичный вектор, перпендикулярный к этой поверхности в каждой точке (n меняет направление при движении вокруг поверхности, но всегда имеет единичную длину); пусть n направлен наружу. Покажем, что

Здесь S указывает, что эти интегралы берутся по всей поверхности, da – элемент поверхности S.

Для простоты мы выберем удобную для нас форму S в виде небольшого параллелепипеда (как показано на рис. 12) со сторонами D x, D y и D z; точка P – центр параллелепипеда. Вычислим интеграл из уравнения (4) сначала по одной грани параллелепипеда. Для передней грани n = i (единичный вектор параллелен оси x); D a = D y D z. Вклад в интеграл от передней грани равен

На противоположной грани n = –i; эта грань дает вклад в интеграл

Используя теорему Тейлора, получим общий вклад от двух граней

Заметим, что D x D y D z = D V. Аналогичным образом можно вычислить вклад от двух других пар граней. Полный интеграл равен

и если мы положим D V ® 0, то члены более высокого порядка исчезнут. По формуле (2) выражение в скобках – это divU, что доказывает равенство (4).

Равенство (5) можно доказать таким же образом. Воспользуемся снова рис. 12; тогда вклад от передней грани в интеграл будет равен

и, используя теорему Тейлора, получим, что суммарный вклад в интеграл от двух граней имеет вид

т.е. это два члена из выражения для rotU в уравнении (3). Другие четыре члена получатся после учета вкладов от других четырех граней.

Что, в сущности, означают эти соотношения? Рассмотрим равенство (4). Предположим, что U – скорость (жидкости, например). Тогда n Ч U da = U_n da, где U_nявляется нормальной компонентой вектора U к поверхности. Поэтому, U_n da – это объем жидкости, протекающей через da в единицу времени, а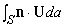 – это объем жидкости, вытекающей через S в единицу времени. Следовательно,

– скорость расширения единицы объема вокруг точки P. Отсюда дивергенция получила свое название; она показывает скорость, с которой жидкость расширяется из (т.е. расходится от) P.

Чтобы объяснить физическое значение ротора U, рассмотрим другой поверхностный интеграл по маленькому цилиндрическому объему высотой h, окружающему точку P; плоско-параллельные поверхности могут быть ориентированы в любом направлении, которое мы выбираем. Пусть k –единичный вектор перпендикулярный к каждой поверхности, и пусть площадь каждой поверхности D A; тогда полный объем D V = h D A (рис. 13). Рассмотрим теперь интеграл

Подынтегральное выражение – уже упоминавшееся ранее тройное скалярное произведение. Это произведение будет равно нулю на плоских поверхностях, где k и n параллельны. На кривой поверхности

где ds – элемент кривой как показано на рис. 13. Сравнивая эти равенства с соотношением (5), получаем, что

Мы по-прежнему предполагаем, что U – скорость. Чему в таком случае будет равна средняя угловая скорость жидкости вокруг k? Очевидно, что

если D A ® 0. Это выражение максимально, когда k и rotU указывают в одном и том же направлении; это означает, что rotU – вектор, равный удвоенной угловой скорости жидкости в точке P. Если жидкость вращается относительно P, то rotU № 0, и векторы U будут вращаться вокруг P. Отсюда и возникло название ротора.

Теорема дивергенции (теорема Остроградского – Гаусса)

Теорема дивергенции (теорема Остроградского – Гаусса) является обобщением формулы (4) для конечных объемов. Она утверждает, что для некоторого объема V, ограниченного замкнутой поверхностью S,

и справедлива для всех непрерывных векторных функций U, имеющих непрерывные первые производные всюду в V и на S. Мы не будем приводить здесь доказательство этой теоремы, но ее справедливость можно понять интуитивно, представляя объем V разделенным на ячейки. Поток U через поверхность, общую для двух ячеек обращается в нуль, и только ячейки, находящиеся на границе S внесут вклад в поверхностный интеграл.

Теорема Стокса

является обобщением уравнения (6) для конечных поверхностей. Она утверждает, что

где C – замкнутая кривая и S – любая поверхность, ограниченная этой кривой. U и ее первые производные должны быть непрерывны всюду на S и C.

Александров П.С. Лекции по аналитической геометрии. М., 1968
Погорелов А.В. Аналитическая геометрия, 3 изд. М., 1968