Параболический треугольник центр тяжести

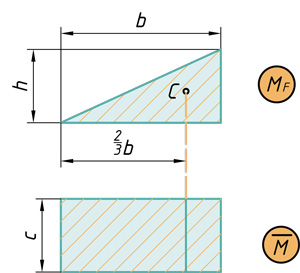
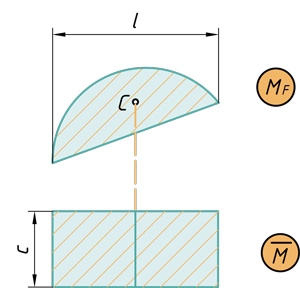
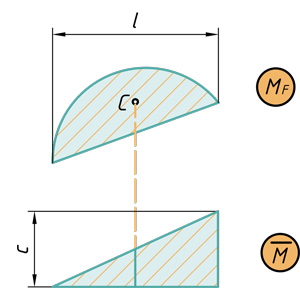
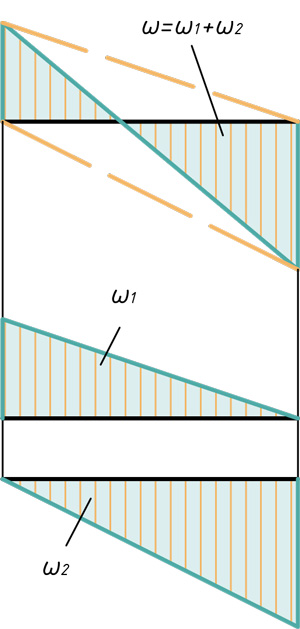
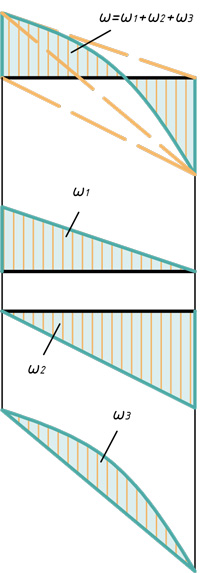
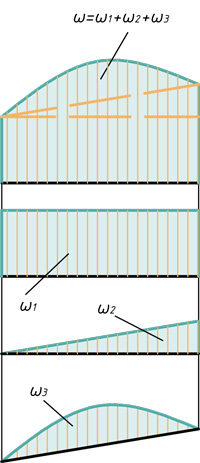
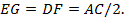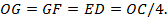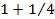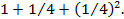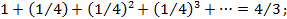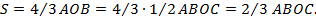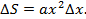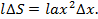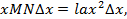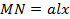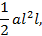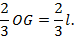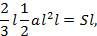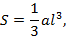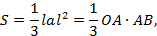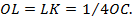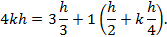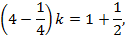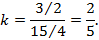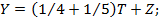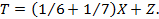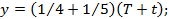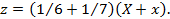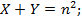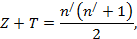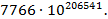При расчетах графоаналитическим методом знание площади эпюры и положения центра тяжести этой эпюры бывает весьма полезным. Ниже представлены наиболее часто встречающиеся виды эпюр, указаны их площади и центры тяжести (ц.т.):

Таблица 378.1 Основные виды эпюр

Примечания к таблице 378.1:

1. В данном случае высота фигуры обозначена литерой q, однако принципиального значения это не имеет, так как и эпюры распределенных нагрузок и эпюры изгибающих моментов и прочие эпюры с точки зрения теории сопротивления материалов равнодостойны.

2. Некоторые эпюры принято отображать не сверху оси (как показано в таблице), а снизу. Это также не имеет принципиального значения, так как не влияет на площадь эпюры и на положение центра тяжести, а только на соответствующий знак.

3. При расчете балок длиной l как правило параметр x = l/2, т.е. представленные эпюры — могут рассматриваться как половины от общих эпюр. Тем не менее приводить полные (симметричные) эпюры не имеет большого смысла, так как центр тяжести таких эпюр будет посредине, а площадь будет такая же, с той только разницей, что в таком случае параметр x = l.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Расчетные данные

Оценка пользователей:10.0 (голосов: 1)Переходов на сайт:8062Комментарии:

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи

Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем, это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.

Верещагин и его метод, правило или способ

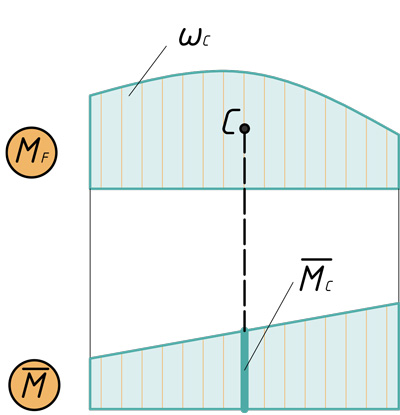
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:​

Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.

Площадь и центр тяжести эпюр

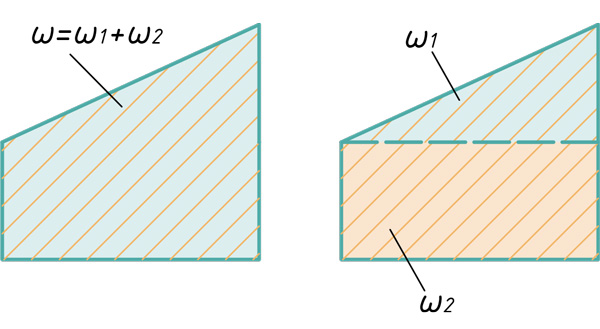
При использовании метода Верещагина, берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.

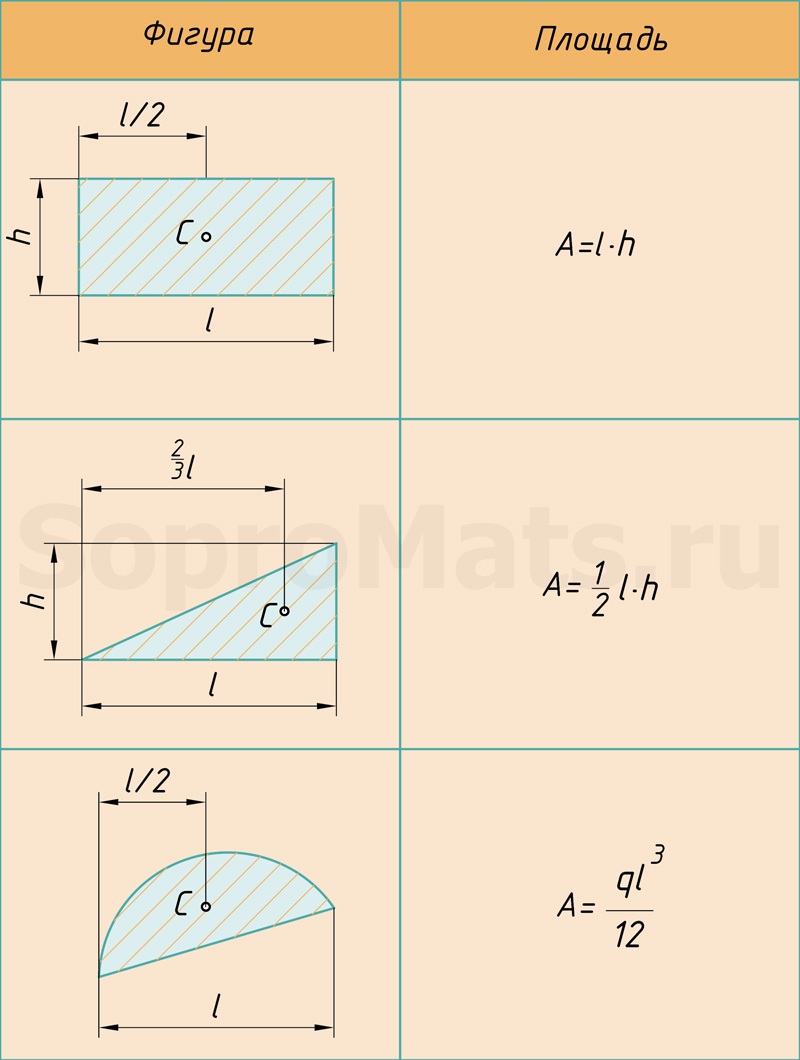
Любую эпюру можно расслоить всего на три фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.

Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:

Перемножение эпюр по Верещагину

В этом блоке статьи покажу частные случаи перемножения эпюр по Верещагину.

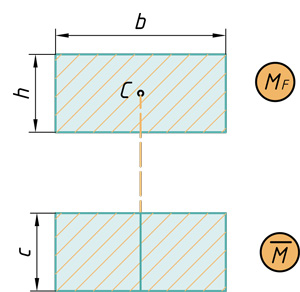
Прямоугольник на прямоугольник

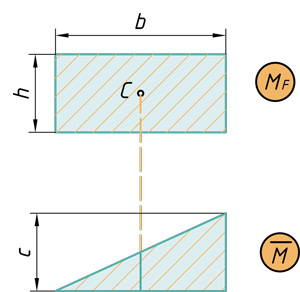
Прямоугольник на треугольник

Треугольник на прямоугольник

Сегмент на прямоугольник

Сегмент на треугольник

Частные случаи расслоения эпюр на простые фигуры

В этом блоке статьи покажу частные случаи расслоения эпюр на простые фигуры, для возможности их перемножения по Верещагину.

Прямоугольник и треугольник

Два треугольника

Два треугольника и сегмент

Треугольник, прямоугольник и сегмент

Пример определения перемещений: прогибов и углов поворотов по Верещагину

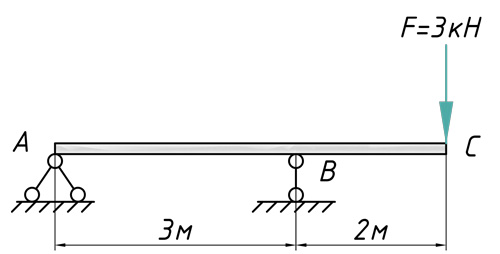
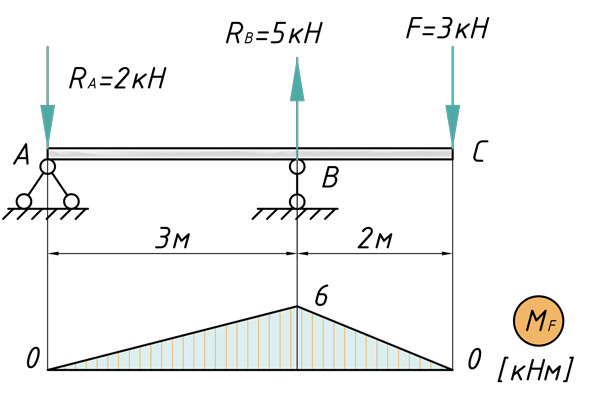
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.

Построение эпюры изгибающих моментов

В первую очередь, рассчитываем и строим эпюру изгибающих моментов:

Построение единичных эпюр моментов

Теперь для каждого искомого перемещений необходимо приложить единичную нагрузку (безразмерную величину равную единице) и построить единичные эпюры:

• Для прогибов, прикладываются единичные силы.
• Для углов поворотов, прикладываются единичные моменты.

Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой силы. Тоже самое касается и углов поворотов.

Перемножение участков эпюры по Верещагину

После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.

Определение прогиба сечения С

Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:

[ _=frac < E_ > (frac cdot 6cdot 3cdot frac cdot 2+frac cdot 6cdot 2cdot frac cdot 2)=frac < 20кН^ >< E_ > ]

Представим, что рассчитываемая балки имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:

Определение угла поворота сечения С

Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:

Тема 3. Архимед. Механические методы определения площадей, объемов и центров тяжести

Архимед был человеком такого возвышенного образа мыслей, такой глубины души и богатства познаний, что о вещах, доставивших ему славу ума не смертного, а божественного, не пожелал ничего написать, но, считая сооружение машин и вообще всякое искусство, сопричастное к повседневным нуждам, низменным и грубым, все свое рвение обратил на такие занятия, в которых красота и совершенство пребывают не смешанными с потребностями жизни. И нельзя не верить рассказам, будто он был тайно околдован некоей сиреной, не покидавшей его ни на миг, а потому забывал о пище и об уходе за телом. Он совершил множество замечательных открытий, но просил друзей и родственников поставить на его могиле лишь цилиндр с шаром внутри и написать расчет соотношения их объемов.

Архимед не придавал большого значения всем сооруженным им машинам, он рассматривал их лишь как простые геометрические игрушки, которыми он занимался в свободное время, и то большей частью по настоянию царя Гиерона , постоянно направлявшего его занятия от чисто интеллектуальных предметов к материальным вещам.

В минуту опасности, грозящей родному городу, Архимед смог выйти из своего «кабинета» и отдать все силы его защите.

Все это настолько красиво, что невольно возникает вопрос: «А верно ли это? Не является ли это легендой, создавшейся вокруг Архимеда?». А что такие легенды действительно создавались, можно видеть тоже из весьма распространенного объяснения того, каким образом Архимед открыл носящий его имя закон: всякое тело, погруженное в жидкость, теряет в своем весе столько, сколько весит жидкость в объеме этого тела. Это объяснение основывается на следующем рассказе римского архитектора Витрувия .

«Когда Гиерон , достигший царской власти в Сиракузах, после удачного завершения своих походов, решил по обету бессмертным богам поместить в одном из храмов богатый венец, он заказал сделать его за определенную плату и отвесил нужное количество золота подрядчику. В назначенный по договору Архимед (3 в. до н. э.) срок тот доставил царю тонко исполненную работу, в точности, видимо, соответствовавшую весу отпущенного на нее золота.

После же того, как царь узнал о том, что часть золота была утаена и при изготовлении венца в него было примешано такое же количество серебра, он, негодуя на нанесенное ему оскорбление и не находя способа доказать эту покражу, обратился к Архимеду с просьбой взять на себя разрешение этого вопроса.

Случилось так, что в то время как Архимед думал над этим, он, садясь в ванну, заметил, что чем глубже он погружается в нее своим телом, тем больше через край вытекает воды. Эта идея послужила ему способом разрешения его вопроса, и он, не медля, вне себя от радости, выскочил из ванны и бросился к себе домой, громко крича, что нашел то, что искал, ибо на бегу он то и дело восклицал по-гречески «эврика, эврика».

Отметим, что в рассказе Витрувия не упоминается о законе Архимеда. В действительности, как можно видеть из «Метрики» Герона Александрийского (около 100 г. н. э.), Архимед считал, что если подлежащее измерению тело удобопереносимо, то нужно сделать прямоугольный сосуд, могущий вместить это тело, наполнить его водой и опустить в него неправильное тело; тогда ясно, что некоторое количество воды выльется так, что какой был объем у опущенного в воду тела, столько воды недостанет в этом вместилище после того, как тело будет из него вынуто.

Если измерить сделавшееся пустым пространство, то можно найти объем опущенного тела, а следовательно, и плотность.

Теперь постараемся представить себе Архимеда освобожденным от наросших легенд. Его ученик Гераклид составил утраченную/теперь биографию своего учителя.

Эта биография была, по-видимому, очень иконописна, так как автор приписал Архимеду даже открытие конических сечений, что никак не может соответствовать действительности. Попробуем восстановить биографию Архимеда, исходя из надежно установленных фактов.

Архимед погиб в 212 г. до н. э. — в год взятия Сиракуз римской армией. Византийский писатель XII в. Цеци сообщает, что он умер 75 лет от роду; на этом основании принято считать, что Архимед родился в Сицилии в 287 г. до н. э. Когда Архимеду было около десяти лет, в Сицилию вторгся знаменитый царь Пирр Эпирский.

В борьбе с Пирром выдвинулся Гиерон , бывший родственником Архимеда, и в 270 г. до н. э. сделавшийся правителем Сиракуз. Первая половина его царствования не была мирной; он втянулся в первую Пуническую войну (264—241 гг. до н. э.), где в союзе с карфагенянами воевал против римлян, но скоро вышел из войны. По окончании войны Сицилия сделалась римской провинцией, Сиракузы еще оставались свободными.

С 241 г. до н. э. начинается мирный период царствования Гиерона , старавшегося поддерживать хорошие отношения как с римлянами, так и с карфагенянами; тем не менее он деятельно готовится к отражению возможных покушений на свободу Сиракуз и усиливает обороноспособность родного города, привлекая к этой работе, как писал Плутарх, и Архимеда.

Таков был фон, на котором развертывалась деятельность Архимеда. Из дошедших до нас полностью сочинений Архимеда рассмотрим следующие .

1. «Квадратура параболы».

2. Две книги «О шаре и цилиндре».

3. «О коноидах и сфероидах».

Эти сочинения представляют законченную группу посланий, написанных Архимедом к некоему Досифею — ученику Конона Самосского, бывшего кем-то вроде научного руководителя Архимеда и давшего ему программу работ, воплощенную в этих посланиях. Порядок написания этих сочинений вполне устанавливается из сопровождающих их введений.

Первое из этих сочинений было написано к Досифею после смерти Конона . Конон Самосский был известен историкам по следующей легенде. В 246 г. до н. э. египетский властитель Птолемей III Эвергет начал Третью Сирийскую войну и отправился в поход на Антиохию ; его супруга Вереника , молясь, за благополучное окончание похода, принесла в жертву богам свои волосы. После окончания похода оказалось, что ее волос в храме нет; тогда придворный астроном Конон заявил, что эти волосы были помещены богами на небе и образовали новое созвездие «Волосы Вереники ». Это событие было воспето придворным поэтом Каллимахом , вследствие чего и стало известным историкам.

Конон был в действительности очень крупным ученым, оказавшим большое влияние на научное развитие Архимеда, который мог познакомиться с ним в Сицилии, где Конон производил астрономические исследования, или в Александрии во время пребывания там Архимеда.

Второй ученый, с которым Архимед поддерживал переписку, был знаменитый Эратосфен Киренский (285—205 гг. до н. э.), который был приглашен в Александрию в 245 г. Птолемеем Эвергетом для воспитания его сына и наследника Птолемея IV Филопатора . Наиболее удобное время для этого посещения наступило после окончания первой Пунической войны, когда правитель Сиракуз Гиерон мог отпустить Архимеда в Александрию.

Легенда о Веренике важна в том отношении, что в 246 г. до н. э. Конон был жив, следовательно, сочинение’ «О квадратуре параболы» было написано после этого года. Но в 246 г. Архимеду шел уже 41 год; таким образом, научной работой Архимеду пришлось заняться уже на склоне лет, приближаясь к пятидесятилетнему возрасту. Обычно историки относят смерть Конона к тридцатым годам III в. до н. э.; тогда предположительно можно было бы отнести «Квадратуру параболы» примерно к 235 г. до н. э.

Определим примерное время остальных произведений Архимеда:

5. Две кциги «О равновесии плоских фигур».

6. « Эфод , или послание к Эратосфену о механических теоремах».

7. Две книги «О плавающих телах».

8. «Измерение круга».

10. «Задача о быках».

Две книги «О равновесии плоских фигур» имеют своей целью определить центр тяжести параболического сегмента; таким образом, они написаны после «Квадратуры параболы».

Во вступлении к « Эфоду » Архимед писал о найденных им теоремах. Эти теоремы оказались отличными от найденных ранее: действительно в прежних теоремах коноидальные и сфероидальные тела, а также их сегменты сравнивались по величине с конусами и цилиндрами, и ни одно из этих тел не оказалось равным телесной фигуре, ограниченной плоскостями; из рассматриваемых же тел, ограниченных двумя плоскостями и цилиндрическими поверхностями, каждое оказывается равным одной из телесных фигур, ограниченных плоскостями.

Таким образом, « Эфод » написан после «Коноидов и сфероидов».

Вторая книга «О плавающих телах» рассматривает положение равновесия сегмента параболоида, для чего необходимо знать положение центра тяжести соответствующего объема. Так как это положение определено в « Эфоде », то книги о плавании написаны после « Эфода ».

Таким образом, порядок этих сочинений можно считать установленным — все они написаны после «Квадратуры параболы».

Оставшиеся три произведения относится к вычислительной математике. Из них особенно интересна книга «Об измерении круги», написанная, как писал сам Архимед, ранее «Псаммита».

В первых четырех указанных сочинениях (в посланиях к Досифею ) Архимед занимается определением поверхностей и объемов различных фигур и тел. Его решение состоит из двух стадий: в первой он решает задачу сначала механическим способом, разбивая исследуемую фигуру на весьма малые части, очень похожие на «неделимые» Демокрита ; получив таким образом решение задачи, он доказывает его строго геометрически, пользуясь методом исчерпания Евдокса , строя последовательные совокупности прямолинейных фигур или пластинок так, чтобы они «исчерпали» всю площадь или объем измеряемой фигуры. В «Квадратуре параболы» он делает это, беря метод исчерпания в его первоначальной форме. Рассмотрим этот метод.

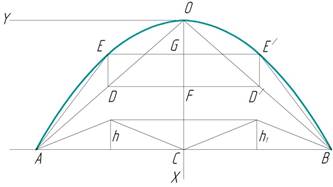
Пусть АОВ (рис. 3) представляет сегмент параболы, площадь которого нужно определить; пусть ОС ось параболы, которую принимаем за ось х, тогда соотношение между абсциссами х и ординатами у параболы будет иметь вид:

y 2 =2 px 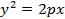(1)

Архимед пользуется свойством параболы, что все ее диаметры параллельны. Он вписывает в параболу треугольник АОВ, вершина которого совпадает с вершиной параболы; площадь этого треугольника примем за единицу. Так как ось Ох — ось параболы, то С — середина прямой АВ, ОС — диаметр сегмента АОВ.

После выделения треугольника АОВ получим еще два сегмента параболы. Разделим хорды ОА и ОВ пополам в точках D и D’ и проведем отрезки DE и D’E’. Соединив прямыми точки Е и E’ соответственно с А, О и В, получим еще два треугольника АЕО и ВE’О. Проведем прямые DD’ и ЕE’ полученная фигура будет, очевидно, параллелограммом.

EG = DF = AC /2.

Но EG представляет ординату, соответствующую абсциссе OG, а АС — ординату для абсциссы ОС. Так как AC=2 EG, то по уравнению (1) параболы

OC = 2 2 OG ,

OG = GF = ED = OC /4.

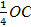
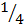
Переместим треугольники АЕО и BE’О параллельно оси Ох так, чтобы они стали основаниями на прямой АВ. Так как высоты ED и ЕD’ равны 1 4 ОС , то нетрудно видеть, что сумма площадей этих треугольников в передвинутом положении равна четверти АОВ, или, поскольку площадь АОВ принята за единицу, 1 4 .

Сумма площадей полученных трех треугольников равна:

1+ 1 4

Если рассмотреть еще четыре сегмента на хордах АЕ, ЕО, ОE’ и Е’В и вписать в них треугольники, то аналогичное рассуждение покажет, что сумма площадей четырех этих треугольников равна 1 4 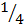суммы треугольников АЕО и ОЕ’В; добавив эти треугольники, получим сумму

1+ 1 4 + 1 4 2 .

Продолжая рассуждать таким же образом, получим, что площадь рассматриваемого сегмента равна сумме геометрической прогрессии:

1+ 1 4 + 1 4 2 + 1 4 3 + … = 4 3 ;

S = 4 3 AOB = 4 3 ∙ 1 2 ABOC = 2 3 ABOC .

Таким образом, если на основании АВ сегмента и его оси ОС построить прямоугольник (параллелограмм), то площадь параболического сегмента будет равна 2/з площади этого параллелограмма.

В книгах «О шаре и цилиндре» наблюдается следующая эволюция метода исчерпания. Определяемая величина заключается между двумя суммами, из которых одна больше, а другая меньше определяемой величины, причем отношение этих сумм может быть сделано сколь угодно близким к единице.

Тот же метод использован в книгах «О спиралях» и «О коноидах и сфероидах», но только теперь определяющее условие заключается в том, что разность этих сумм может быть сделана сколь угодно близкой к нулю.

Так как в книге «Об измерении круга» употребляется третья форма метода исчерпания, то имеются все основания полагать, что эта книга была написана не ранее сочинений «О спиралях» и «О коноидах и сфероидах». Кроме того, интересна близость тем книги «О спиралях» и «Измерения круга»: и та и другая касаются определения длины окружности, но только в первой книге длина окружности получается при помощи построения, а во второй — при помощи вычисления.

Таким образом, самым ранним из сохранившихся полностью сочинений Архимеда является «Квадратура параболы», написанная им в возрасте 45 лет. Чем же занимался Архимед ранее? В рассказе Полибия об осаде Сиракуз говорится, что первая Пуническая война не разрешила вопроса о форме отношений между Римом и Карфагеном. Карфагеняне не могли примириться с потерей Сицилии, а немного позже и Сардинии с Корсикой, захваченных Римом.

В 218 г. до н. э. началась вторая Пуническая война походом. Ганнибала из Испании через Альпы на Италию. Ряд блестящих побед Ганнибала, из которых наиболее важной была победи, одержанная при Каннах (216 г. до н. э.), поставил Рим в очень тяжелое положение, но все же римляне не сдавались. Ганнибалу пришлось искать союзников. На следующий год после победы при Каннах умер девяностолетний Гиерон, сохранивший верность Риму, но после его смерти в Сиракузах одержала верх антиримская партия и Сиракузы примкнули к восстанию греческих колоний в Сицилии. Против Сиракуз отправили войско под командой Аппия Клавдия и флот под командованием Марка Марцелла. Римляне хотели взять Сиракузы первым же приступом, надеясь при многочисленности рабочих рук покончить с приготовлениями в течение пяти дней. Но при этом они не приняли в расчет искусства Архимеда, не догадались, что иногда дарование одного человека способно сделать больше, чем огромное множество рук. Архимед заготовил внутри города, а равно и против нападающих с моря, такие средства обороны, что защитникам не было необходимости утруждать себя непредусмотренными работами на случай неожиданных способов нападения; у них заранее готово было все к отражению врага в любом случае.

Дальше Полибий рассказывает о нападении римского флота с моря. Архимед соорудил машины, приспособив их к метанию снарядов на любое расстояние. Так, если неприятель подплывал издали, то Архимед поражал его из дальнобойных камнеметальниц тяжелыми снарядами или стрелами и повергал его в трудное положение. Когда же снаряды начинали летать поверх неприятеля, то Архимед применял меньшие машины, каждый раз сообразуясь с расстоянием, и наводил на римлян такой ужас, что они никак не решались идти на приступ или приблизиться к городу на судах. Наконец, Марк (Марцелл), раздосадованный неудачами, вынужден был сделать попытку тайком ночью подойти к городу на кораблях. Когда римляне подошли к берегу на расстояние выстрела, Архимед употребил другое средство, направленное против воинов, сражавшихся с судов, а именно: он велел сделать э стене приблизительно на высоте человеческого роста множество отверстий, с наружной стороны имевших в ширину пальца четыре; у отверстий изнутри стены поставил стрелков, через отверстия обстреливал корабельных воинов и тем отнимал у них всякую возможность сделать что-нибудь. Таким образом, далеко или близко находился неприятель, Архимед не только разрушал все его планы, но и производил в его рядах большие опустошения.

В настоящее время то, что сделал Архимед, называется пристрелкой по квадратам: вся местность, окружающая крепость, делится на квадраты и для каждого квадрата определяется возвышение (угол с горизонтом дула) для орудия, из которого должен производиться выстрел. Разница заключается лишь в том, что во времена Архимеда вместо изменения возвышения надо было пользоваться изменением калибра орудия. Во всяком случае, когда неприятель показывался в каком-либо квадрате, пускались в ход орудия калибра, соответствующего этому квадрату. Такого рода пристрелка предполагает долгую предварительную работу по определению расстояний для различных квадратов и по подбору наилучшего калибра орудий.

Когда корабль приближался к городской стене, то, кроме действия метательных орудий, с машины спускалась прикрепленная к цепи железная лапа; управляющий жерлом машины захватывал в каком-либо месте этой лапой нос корабля и потом опускал вниз находящийся внутри города конец машины. Когда нос судна был таким образом поднят и судно поставлено отвесно на корму, то плечо рычага закреплялось неподвижно, а лапа вместе с цепью отделялась от машины освобождающим приспособлением. Вследствие этого некоторые суда ложились на бок, другие совсем опрокидывались, большинство же от падения в море носом со значительной высоты погружались и наполнялись водой, внося большой беспорядок и ужас среди экипажа. Изобретательность Архимеда приводила Марка в отчаяние; с прискорбием он видел, что осажденные глумятся над его усилиями и причиняют ему большие потери.

Римляне сильно страдали от камнеметальниц и катапульт, из которых их обстреливали; сиракузяне имели в запасе множество превосходных и метких метательных орудий, на которые царь Гиерон дал средства, а Архимед изобрел и мастерски построил машины.

Расчет машин, подымающих корабли, немыслим без учета потери веса корабля, погруженного в море; это можно сопоставить с открытием закона Архимеда.

Рассмотрим теперь подробно две книги Архимеда «О равновесии плоских фигур» (или о центре тяжести плоских фигур). Считают, что первая книга этого произведения посвящена теории рычага; некоторые авторы полагают даже, что эта книга, взятая в отдельности, является первым произведением Архимеда, а вторая книга, содержащая определение центра тяжести параболического сегмента, представляет самостоятельное произведение.

Однако в первой книге определяются только центры тяжести тех плоских фигур (параллелограмм, треугольник), которые нужны для доказательства теорем второй книги. Кроме того, многие положения во второй книге являются обобщением, сделанным на основании мыслей, изложенных в первой книге (первое предложение второй книги является обобщением пятого и шестого предложений первой книги). Первую книгу нельзя считать первым сочинением на рассматриваемую тему, так как в ней не дано самого главного — определения центра тяжести. Это было сделано в произведении, предшествовавшем созданию «Квадратуры параболы», в котором имеются ссылки на это произведение. Отрывки из него сохранились в «Механике» Герона Александрийского и «Математической библиотеке» Паппа. Наиболее важным из этих отрывков является сформулированное Архимедом определение понятия о центре тяжести: центром тяжести тела называется расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно остается в покое и сохраняет первоначальное положение.

Законы равновесия выводятся Архимедом из следующие допущений, помещенных в начале первой книги «О равновесии».

1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.

2. Если при равновесии тяжестей на каких-либо длинах к одной из тяжестей что-либо прибавить, то они не будут уравновешиваться, но перевесит та тяжесть, к которой прибавлено.

3. Если от одной из тяжестей отнять что-либо, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято.

4. При совмещении друг с другом равных и подобных плоских фигур совмещаются друг с другом и их центры тяжести.

5. У неравных, но подобных фигур центры тяжести располагаются подобно.

6. Если величины уравновешиваются на каких-либо длинах, то на тех же длинах уравновешиваются и величины, равные им.

7. Во всякой фигуре, периметр которой везде выпукл в одну и ту же сторону, центр тяжести находится внутри фигуры.

Приведем доказательство Архимеда в той форме, которую придал ему Галилей.

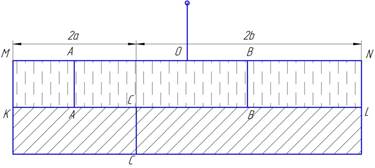
Пусть в точке О подвешено за середину коромысло MN имеющее длину 2(а+b) (рис. 4).

К этому коромыслу при помощи бесконечного множества вертикальных веревочек прикреплена однородная балка KL такой же длины 2(а+b). Вся система будет, очевидно, в равновесии, которое не нарушится, если разрежем балку по линии СС на два отрезка: КС — длины 2 а и CL — длины 2 b. После этого обрежем все веревки, кроме двух: АА и ВВ, находящихся в серединах отрезков КС и CL, отчего равновесие тоже не нарушится. Таким образом, величина КС = 2 а на плече АО = b будет уравновешивать величину CL на плече ОВ — а. Иными словами, при равновесии грузы, приложенные в A и В, будут обратно пропорциональны соответствующим плечам.

Равновесие не нарушится, если обе отрезанные части повернем вокруг осей АА и ВВ на любые углы; именно это и предполагает допущение 6, равносильное такой формулировке. Действие груза, приложенного в данной точке, определяется только его величиной, т. е. совершенно не зависит от формы или ориентации этого груза.

Возможность поворачивания обеих осей балки вокруг осей АА и ВВ имеет место лишь при требуемом Махом законе пропорциональности моментов длине плеча в первой степени и исключает другие законы, например квадратичную зависимость; поэтому доказательство Архимеда является вполне строгим.

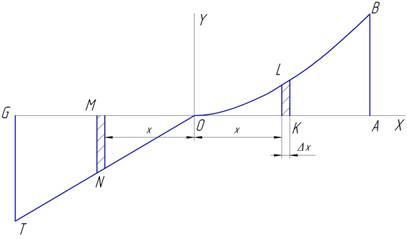
Закон равновесия рычага используется Архимедом в качестве основы метода геометрического интегрирования, изложенного им в «Эфоде», как средство для исследования и предварительного решения задач. Покажем его на простом примере, а именно на рассмотренной выше квадратуре параболического сегмента, но только сделаем упрощение: будем находить не площадь сегмента, равную двум третям параллелограмма, а площадь, которая остается у параллелограмма, если вырезать из него этот сегмент. Тогда задачу можно сформулировать в таком виде: найти площадь, заключенную между осью абсцисс, дугой параболы, заданной уравнением y = a x 2 , и ординатой, соответствующей абсциссе ОA= l (рис. 5).

Возьмем равноплечий рычаг AOG длиной 2 l с точкой опоры О; на одном из его плеч расположим площадь ОАВ и разобьем ее на ряд весьма тонких полосок шириной Δ x. Пусть KL — одна из этих полосок, соответствующая абсциссе ОК = х; тогда ордината KL = у выразится ах 2 и вся площадь полоски

∆ S = ax 2 ∆ x .

Сдвинем ее на конец рычага А; момент этой полоски относительно точки О равен

l ∆ S = l ax 2 ∆ x .

Попробуем уравновесить этот момент, подвешивая с левой стороны рычага на том же расстоянии х полоску MN такой же ширины Δх. Длина соответствующей ординаты MN определится сравнением моментов обеих полосок относительно О:

xMN ∆ x = l ax 2 ∆ x ,

откуда MN = alx

Поступая так с каждой полоской, на левом плече рычага получим ряд полосок, непрерывно распределенных по длине GO. Так как ординаты этих полосок пропорциональны расстояниям х, то концы их расположатся по прямой линии ONT; величина крайней ординаты GT = аl 2 .

Площадь S = ОАВ, сосредоточенная на конце A, уравновешена прикрепленным к стороне OG треугольником OGT. Площадь этого треугольника равна

1 2 a l 2 l ,

a расстояние его центра тяжести от вершины О:

2 3 OG = 2 3 l .

Сравнивая момент этого треугольника относительно О с моментом относительно той же точки, сосредоточенной в точке А искомой площади S, получим

2 3 l 1 2 a l 2 l = Sl ,

S = 1 3 a l 3 ,

S = 1 3 la l 2 = 1 3 OA ∙ AB ,

что совпадает с найденным выше результатом.

Успех вывода получается в результате понижения степени рассматриваемой кривой — определение величины площади, ограниченной двумя прямоугольными отрезками и кривой второй степени, сводится к определению центра тяжести площади, ограниченной кривой первой степени, т. е. прямой. Этот метод приложим, очевидно, к кривым, уравнение которых имеет вид у = ax h .

Кроме перечисленных произведений, дошедших до нас полностью, сохранились отрывки более ранних произведений Архимеда, имеющиеся в «Механике» Герона и в 8-й книге «Библиотеки» Паппа.

У Герона есть отрывок из сочинения Архимеда «Книга опор», где не замечается никаких следов понятия о центре тяжести. Он пишет: если балка оперта по концам, то на каждую опору падает половина веса; если имеется еще третья опора между концами, то на нее падают по половине веса балки в обоих соседних пролетах; таким образом, средняя опора несет половину веса всей балки независимо от того, в каком месте она помещена.

Из книги Архимеда, название которой установить трудно (то ли это «О рычагах», то ли «О равновесии» или «Механика»), имеются большие отрывки: один в «Механике» Герона (книга I, стр. 24), а другой в «Математической библиотеке» Паппа (книга VIII, стр. 5—8). Эти отрывки показывают, как доказывались существование и единственность центра тяжести твердого тела произвольной формы.

Архимед рассматривает вертикальную плоскость ABCD, ограниченную сверху горизонтальной прямой АВ. Если на эту прямую положить тяжелое тело, то оно может оказаться в таком положении, что будет оставаться в покое, не вращаясь и не падая вниз. Если теперь мы мысленно продолжим плоскость ABCD, то она рассечет лежащее тело на две части, обладающие одинаковыми моментами и взаимно уравновешивающиеся. Если затем переставить груз так, чтобы он касался прямой АВ другой своей частью, то можно дать ему такое положение, что он, будучи опущен, останется в покое и не упадет. Если снова вообразить плоскость ABCD продолженной, то она тоже разделит груз на две взаимно уравновешивающиеся части и пересечется первой плоскостью, делившей тот же груз на две взаимно уравновешивающиеся части; если бы эти плоскости не пересекались, то те же самые части были бы и уравновешивающимися, и неуравновешивающимися, что нелепо.

Вообразим прямую АВ, перпендикулярную к горизонтальной плоскости; положим груз на точку А так, чтобы он, пользуясь прямой АВ как подставкой, оставался в покое. Если продолжить прямую АВ, то некоторая ее часть будет находиться внутри рассматриваемого тела. Снова наложим его на эту прямую другой частью так, чтобы оно опять стало неподвижным; тогда продолженная прямая АВ пересечется первоначально заключавшимся внутри тела отрезком.

Действительно, если бы она не пересеклась, то оказалось бы возможным, что некоторые плоскости, проведенные через каждую из этих прямых, не пересекаются друг с другом внутри тела, причем каждая из них разделяет груз на части, которые одновременно являются и уравновешивающимися, и неуравновешивающимися, что бессмысленно; следовательно, упомянутые прямые пересекутся внутри тела.

Если в других положениях помещать груз на точку А так, чтобы он оставался в покое, то снова продолженная прямая АВ обязательно пересечется заключающимися внутри тела отрезками первоначальных прямых. Из этого ясно, что такие воображаемые прямые пересекают друг друга в одной и той же точке; эта точка и называется центром тяжести.

Как следствие отсюда получается, что закрепленное в этой точке тело остается в равновесии в любом положении.

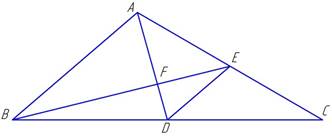
Вышеописанная методика применяется и в приведенных Героном («Механика», книга II, стр. 35—36) правилах нахождения центра тяжести различных плоских фигур. Для этого определяем центр тяжести, треугольника, равномерного по толщине и однородного по весу. Пусть дан треугольник ABC (рис. 6). Разделим линию ВС пополам в точке D и соединим А и D. Если опереть треугольник на линию AD, он не будет иметь момента ни в ту, ни в другую сторону, так как треугольники ABD и ADC равны. Точно так же если разделить линию АС в точке Е и соединить точки В и E, то, если опереть треугольник на линию ВЕ, он также не наклонится ни в ту, ни в другую сторону. Так как треугольник, будучи оперт на каждую из линий AD и BE, находится в равновесии своих частей и не наклоняется ни в ту, ни в другую сторону, то общая точка F, в которой эти две линии пересекаются, является центром тяжести.

Так как треугольники ABD и ADC равны, это заставило некоторых исследователей думать, что Архимед или кто-либо из его предшественников считал, что центр тяжести плоской фигуры будет точка, в которой пересекаются прямые, делящие площадь фигуры на две равные части. Невозможность такого предположения сразу же устанавливается, если прочесть, как определяется центр тяжести четырехугольника.

Пусть дан четырехугольник ABCD (рис. 7). Соединим точки В и D и разделим BD пополам в точке Е; соединим также А и Е, Е и С и разделим линии АЕ и ЕС в точках F и Н таким образом, чтобы АЕ была равна удвоенной величине FE, а СН — удвоенной НЕ. Тогда центр тяжести треугольника ABD — точка F, а центр треугольника BDC — точка Н.

Получим то же самое, если представлять треугольник ABD сосредоточенным в точке F а треугольник BCD — в точке H. Тогда линия FH становится коромыслом, на концах которого находятся эти величины. Поэтому если разделить линию FH в точке G таким образом, чтобы GH относилось к FG как вес F, т. е. вес треугольника ABD к весу Н — к весу треугольника BDC, то точка G, в которой оба веса уравновешиваются, является центром тяжести этого четырехугольника.

Момент веса F равняется сумме моментов весов всех частей треугольника ABD, иными словами, в распоряжении Архимеда был весь материал современной теории параллельных сил. Поэтому при передаче результатов, полученных Архимедом, можно пользоваться современным изложением при непременном условии сохранения его чертежа.

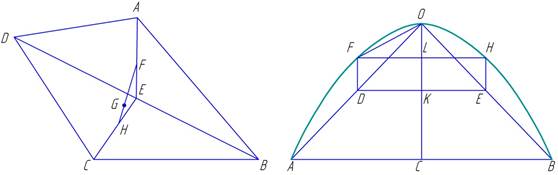
Покажем, как Архимед определял центр тяжести сегмента параболы (предложение VIII второй книги «О равновесии плоских фигур»).

Пусть дан параболический сегмент АОВ с вершиной О (рис. 8). Проведем диаметр ОС и впишем в параболу треугольник AОВ. Выше показано, что площадь сегмента параболы равна 4/з треугольника АОВ. Предположим, что эта площадь равна трем, тогда площадь остающихся сегментов параболы AOF и ВОН будет равна единице. Разделим хорды ОА и ОВ пополам; проведем диаметры FD и НЕ, а также прямые DE и FH. Здесь

DK = FL = 1 2 AC , 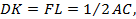а OL = LK = 1 4 OC .

Пусть ОС = h; центр тяжести параболического сегмента лежит на ОС, а сегментов AFO и ОВН — соответственно на диаметрах FD и ЕН.

Предположим, что расстояние от центра сегмента АОВ до основания АВ равняется kh, где k — неопределенный коэффициент; равным образом расстояния от прямой DE центров тяжести сегментов AOF и ВОН равны: kFD = k h 4 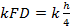—. Далее высота центра тяжести треугольника АОВ над основанием АВ равна 1/3 h, а расстояние СК = h/2. Получим теперь, что момент площади сегмента АОВ относительно АВ равен сумме моментов площадей треугольника АОВ и обоих сегментов AFO и ВНО. В таком случае

4 k h =3 h 3 +1 h 2 + k h 4 .

Сокращая это выражение на А, после очевидных упрощений получаем

4 — 1 4 k =1+ 1 2 ,

k = 3 2 15 4 = 2 5 .

Таким образом, центр тяжести параболического сегмента находится на диаметре на расстоянии 2/5 его длины от основания. Второй работой Архимеда, имеющей определенное отношение к механике, является книга «О спиралях». В самом ее начале интересна терминология, показывающая развитие понятия о скорости. Как существительное «скорость» во времена Архимеда еще не употреблялось: было прилагательное, которое употреблялось как «более или менее скорый» и «равноскорый»; так назывались движения, при которых в одно и то же время проходились одинаковые пути, независимо от того, как эти движения происходили. Для обозначения равномерности движения Архимед употреблял выражение «равно- скоро само с собой», т. е. равноскорыми должны быть движения во всех промежутках времени, на которые можно подразделить все движение.

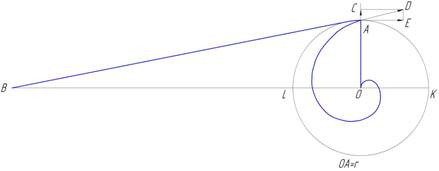
Основная тема этого произведения заключается в задаче: построить прямую, длина которой равнялась бы длине окружности. Для решения Архимед пользуется кинематическим методом; он строит кривую, так называемую архимедову спираль, радиус-вектор которой изменяется пропорционально полярному углу (рис. 9).

Пусть точка О представляет полюс спирали, радиус-вектор которой за время первого оборота сделался равным r = ОА, а прямая AD является касательной к спирали в точке А. Спираль образуется в результате сложения двух движений: равномерного — прямолинейного по прямой ОАС и равномерного — кругового. Если бы точка, описывающая прямую, остановилась, придя в точку А, то в переносном вращении она описала бы изображенную на чертеже окружность AKL с радиусом r.

Пусть АС и АЕ представляют весьма малые перемещения точки, описывающей спираль, в обоих составляющих движениях — по радиусу и перпендикулярно к нему по окружности. При сложении этих движений описывающая спираль точка из положения А перейдет в точку D и прямая AD будет касательной к спирали. Перпендикулярно к радиусу ОА проведем прямую ОВ и продолжим касательную AD до пересечения ее этой прямой в точке В. В начале первого оборота прямая занимала положение ОАС; от ОА отсчитывались углы поворота вращающейся прямой.

По истечении времени первого оборота прямая придет в первоначальное положение, угол поворота станет равным 360° и точка А вращающейся прямой опишет окружность радиусом r. Таким образом, путь, пройденный точкой А в относительном движении по радиусу за время первого оборота, равен ОА, а в переносном движении по окружности — ее длине. Но эти пути относятся как скорости, или как перемещения за один и тот же промежуток времени, т. е. как АС и АЕ. Из подобия треугольников AED и BOA получаем:

AE : ED = BO : OA .

Иными словами, если ОА — путь, пройденный точкой в прямолинейном относительном движении, то ВО — путь, пройденный за то же время точкой А в переносном движении, т. е. длина окружности AKLA.

Треугольник AED, по существу, представляет дифференциальный треугольник Барроу — Ньютона, и не исключена возможность, что понятие об этом треугольнике появилось у Исаака Барроу в результате чтения сочинений Архимеда, которые с переделанными доказательствами были им изданы в 1675 г. Во всяком случае изучение сочинений Архимеда математиками XVII в. было необходимой подготовительной работой к появлению классического анализа бесконечно малых.

Последним произведением Архимеда является его сочинение «О плавающих телах». В первой книге он устанавливает основные законы равновесия тел в жидкости и рассматривает условия равновесия сферического сегмента, погруженного в воду, поверхность которой он считает тоже сферической, как поверхность реальных земных морей. Во второй книге он формулирует носящий его имя закон и затем рассматривает условия равновесия плавающего в жидкости сегмента параболоида вращения, причем поверхность жидкости теперь уже считается плоской.

В основе его рассуждений лежат теоремы, определяющие величину объема и положение центра тяжести сегмента параболоида вращения.

При погружении тяжелого твердого тела в жидкость, плотность которой больше плотности тела, оно опускается в жидкость так, чтобы поверхность жидкости (так называемая плоскость плавания) отсекала от тела объем, вес жидкости в котором равнялся весу тела.

Если построить все плоскости плавания для различных положений плавающего тела, то огибающая всех таких плоскостей будет некоторой поверхностью, которая называется поверхностью сечений.

Центры тяжести объемов, отсекаемых плоскостями плавания, образуют поверхность, называемую поверхностью центров.

Для этих поверхностей имеются такие теоремы.

1. Плоскость плавания касается поверхности сечений в центре тяжести фигуры, отсекаемой поверхностью тела на плоскости плавания.

2. Касательная плоскость к поверхности центров параллельна соответствующей плоскости плавания.

Для нахождения всех плоскостей плавания в положениях равновесия плавающего тела нужно из центра его тяжести опустить нормали к поверхности центров и провести соответствующее этим нормалям плоскости сечения. Эти плоскости и будут искомыми плоскостями плавания.

Архимед рассматривал только те положения равновесия, когда основание сегмента находится или полностью вне поверхности жидкости (вершина сегмента обращена вниз), или полностью внутри жидкости (сегмент плавает с вершиной над поверхностью жидкости).

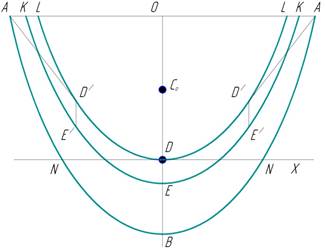
Так как сегмент принадлежит параболоиду вращения, то эту задачу можно свести к плоской, заменив все поверхности линиями, представляющими их сечения плоскостью, проведенной через ось параболоида. Обозначим сечение данного сегмента ABA, его ось ОВ, основание АОА и центр тяжести С₀( ОС₀ = l/3 ОВ) (рис. 10). Пусть NN— сечение сегмента поверхностью жидкости, DB — ось погруженной части, a E( DE = l/3 DB) —центр тяжести объема погруженной части.

Поверхность сечений изобразится параболой LDL, вершина которой D находится на поверхности жидкости; эта парабола представляет параболу ABA, сдвинутую вверх на расстояние BD. Чтобы получить поверхность центров, нужно через точку Е провести такую же параболу КЕК. Если Архимед рассматривает случай, когда основание АОА находится над поверхностью жидкости, то ему нужны часть D’DD’ параболы сечений, ограниченная точками D’, D’, касательные в которых проходят через конец А основания, а также соответствующая часть Е’ЕЕ’ параболы центров ( D’E’ параллельна ОВ). Продолжить далее эти поверхности для него нельзя, так для этого пришлось бы определить объем сегмента, отсеченный плоскостью, которая пересекает как боковую поверхность сегмента, так и плоскость основания, а эта задача им не решалась.

Если требуется определить положение равновесия сегмента, плавающего вершиной вверх, то надо определять объем и центр тяжести погруженной части сегмента, которая будет иметь вид ANNA, иными словами, представит разность двух параболических сегментов BNN и ВАА. Основываясь на этом, можно построить новые кривые сечений и центров, которые тоже будут некоторыми параболами.

Далее следует рассматривать моменты пары, образованной весом сегмента и силой давления вытесненной воды, приложенной в центре тяжести погруженной части; равновесие имеет место, когда при отклонении от положения равновесия этот момент оказывается восстанавливающим. Таким образом, Архимед получает только положения устойчивого равновесия.

Разница между методом Архимеда и современным методом заключается в том, что сейчас плотность жидкости принимают постоянной и изменяют размеры рассматриваемого сегмента, а Архимед сохраняет постоянным положение тела, но изменяет плотность жидкости. Его методика, по существу, мало отличается от методики, выработанной в XIX в. при помощи теорем Дюпена.

Из этого не следует делать вывода о тождественности этих методов, как это делают некоторые исследователи, находящие у Архимеда даже понятие о метацентре, установленное лишь в XVIII в.

Основное различие заключается в том, что Архимед не мог построить поверхности сечений для всех положений тела относительно поверхности жидкости, а следовательно, и не знал ее, так как у греков построяемость была критерием существования того или другого геометрического образа или операции. Силой своего гения Архимед смог подняться до высот, достигнутых наукой в XIX в.

Для полной характеристики Архимеда следует отметить, что Архимед нашел значение π = 22 7 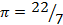. Что же заставило его найти числовое выражение отношения окружности к диаметру, тем более что он уже имел построение, позволяющее найти прямую, равную длине заданной окружности?

В истории европейской науки около 1600 г. математики тоже стремились найти более точное значение числа π. Это было время, когда Адриан Меций нашел значение π = 355 113 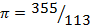, а Лудольф из Кельна вычислил число π с точностью до 36-го десятичного знака. Виллиброд Снеллий открыл метод триангуляции и применил его к определению размеров Земли.

Не было ли чего-нибудь подобного и во времена Архимеда? Тит Ливии, описывая осаду Сиракуз в 24-й книге своей истории Рима, называет Архимеда «единственным в своем роде созерцателем неба и светил». О найденной числовой величине я Архимед вспоминает в «Псаммите», где идет речь об определении размеров мира и вычислении количества песчинок, которые могли бы заполнить объем мира. Он проводит также наблюдения, чтобы вычислить величину Солнца и расстояние от него до Земли. Свои наблюдения он применяет к центру Земли; между прочим это первое появление в истории астрономии понятия о так называемом параллаксе; ближайший предшественник Архимеда Аристарх Самосский, проводя эти же наблюдения на поверхности Земли, считал, что они дают такие же результаты, как если бы наблюдения производились из центра Земли.

Для определения потребного количества песка Архимед создал систему счисления, при помощи которой можно было изображать очень большие числа. Этим занимался не один он: систему счисления больших чисел создавал его младший современник Аполлоний Пергский. Правда, инженерный ум Архимеда не ограничился простым вычислением; он, не придававший большого значения построенным им машинам, описал только одну из них — построенную им «астрономическую сферу». Эта сфера после взятия Сиракуз римлянами досталась в качестве добычи Марку Марцеллу, поместившему ее в Храме Доблести и сохранившему для себя лишь второй, меньший экземпляр.

В диалоге Цицерона «О государстве» одно из действующих лиц Сульпиций Галл (тоже занимавшийся астрономией и предсказавший даже лунное затмение) показывает эту сферу. Слушавший его рассказчик говорил об Архимеде, что в этом сицилийце был гений, равняться с которым человеческая природа не казалась способной. Для возможности представлений движений Солнца, Луны и пяти звезд ему пришлось отказаться от употребления сплошной сферы, на которой было бы невозможно их воспроизвести, и придумать другую совершенно отличного вида.

В изобретении Архимеда чудесным было искусство, в котором он мог объединить в одной системе и воспроизвести при помощи одного вращения все очень отличающиеся друг от друга движения и различные периоды обращения различных светил. Когда Галл приводил сферу в движение, то при каждом обороте можно было видеть, как Луна появлялась вслед за Солнцем на земном горизонте; как она появляется каждый день на небе; далее можно было видеть, как Солнце исчезало на небе и затем понемногу Луна погружалась в земную тень в тот самый момент, когда Солнце находилось с противоположной стороны.

С большими числами связано еще одно сочинение Архимеда, найденное в XVIII в. и опубликованное в 1773 г. известным немецким писателем Лессингом. Это так называемая «Задача о быках», посланная Архимедом на разрешение александрийским ученым, занимающимся подобными вопросами:

Сколько у Солнца быков, найди для меня, чужестранец?

(Ты их, подумав, считай, мудрости если не чужд).

Как на полях Тринакрийской Сицилии острова тучных

Их в четырех стадах много когда-то паслось.

Цветом стада различались: блистало одно млечнобелым,

Темной морской волны стада другого был цвет.

Рыжим третие было, последнее пестрым. И в каждом

Стаде была самцов множества тяжкая мощь.

Если Х, Y, Z и Т обозначим числа белых, черных, рыжих и пестрых быков, то они должны удовлетворять следующим уравнениям:

X = 1 2+ 1 3 Y + Z ; 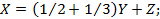Y = 1 4 + 1 5 T + Z ;

T = 1 6+ 1 7 X + Z .

Если x, y, z и t обозначим числа коров тех же цветов, то получим еще четыре уравнения:

x = 1 3+ 1 4 Y + y ; 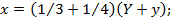y = 1 4+ 1 5 T + t ;

t = 1 5+ 1 6 Z + z ; 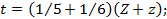z = 1 6+ 1 7 X + x .

Сколько у Солнца быков, чужестранец, коль точно ты скажешь,

Нам раздельно назвав числа тучных быков,

Так же раздельно коров, сколько каждого цвета их было,

Не назовет хоть никто в числах невеждой тебя,

Все ж к мудрецам причислен не будешь.

Эти неопределенные уравнения решить можно; наименьшие значения неизвестных, удовлетворяющих их, выражаются семи- и восьмизначными числами. Этого Архимед не считает достаточным для того, чтобы заслужить название мудреца. Поэтому он добавляет еще два условия:

1. Сумма быков белого и черного цвета должна быть точным квадратом:

X + Y = n 2 ;

2. Сумма пестрых и рыжих быков должна быть равна некоторому треугольному числу:

Z + T = n / n / +1 2 ,

где п и п’ — некоторые целые числа.

После этого Архимед продолжает:

Если ты это найдешь, чужестранец, умом пораскинув,

И сможешь точно назвать каждого стада число,

То уходи, возгордившись победой, и будет считаться,

Что в этой мудрости все ты до конца превзошел.

Решением этих задач занимались ряд математиков. В немецком переводе издания Архимеда Th. Heath указывается порядок общего числа быков:

7766 ∙ 10 206541 .

Архимед поставил задачу, которая, как он знал, практически не может быть разрешена.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

💥 Видео