В треугольнике abc угол c 90 ac 3 см bc 4 см постройте вектор

Инструментарий для оценивания знаний 9 класс УМК Атанасян Л.С.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Скачать:

Видео:№121. В треугольнике ABC дано: ∠C = 90°, AC = 6 см, ВС = 8 см, СМ — медиана. Через вершину ССкачать

Предварительный просмотр:

1. Начертите четыре попарно неколлинеарных вектора . Постройте вектор .

2 . Упростите выражение: .

1. Начертите пять попарно неколлинеарных векторов . Постройте вектор .

2. Упростите выражение: .

Вариант III
(для более подготовленных учащихся)

1. Найдите вектор из условия: .

2. Медианы треугольника ABC пересекаются в точке М . Докажите, что .

Дан прямоугольный треугольник ABC с гипотенузой BC . Постройте вектор и найдите , если AB = 8 см.

Дан прямоугольный треугольник ABC с гипотенузой АВ . Постройте вектор и найдите , если BС = 9 см.

Вариант III
(для более подготовленных учащихся)

Дана трапеция ABCD с основаниями АD и BC . Постройте вектор и найдите , если АD = 12 см, BC = 5 см.

1. Начертите два неколлинеарных вектора и так, что = 3 см, = 2 см. Постройте

2. Четырехугольник KMNP – параллелограмм. Выразите через векторы и векторы и , где А – точка на стороне PN , такая, что PA : AN = 2 : 1, B – середина отрезка MN .

1. Начертите два неколлинеарных вектора и так, что = 2 см, = 3 см. Постройте вектор

2. В параллелограмме ABCD точка M – середина стороны CD ; N – точка на стороне AD , такая, что AN : ND = 1 : 2. Выразите векторы и через векторы и .

Вариант III
(для более подготовленных учащихся)

1. В треугольнике ABC угол C = 90°, AC = 3 см, BC = 4 см. Постройте вектор

2. В трапеции ABCD AB || CD , AB = 3 CD . Выразите через векторы и векторы и , где M – середина стороны BC , а N – точка на стороне AB , такая, что AN : NВ = 2 : 3.

Точка K делит отрезок MN в отношении MK : KN = 3 : 2. Выразите вектор через векторы и , где A – произвольная точка.

Точка A делит отрезок EF в отношении EA : AF = 2 : 5. Выразите вектор через векторы и , где K – произвольная точка.

Решить задачи № 912 (а, г); № 920 (г); № 988 (а, б); № 921 (а, в);
№ 914 (а).

Решить задачи №№ 912 (в, д); 920 (д); 988 (в, г); 921 (б, г); 914 (б).

1. Найдите координаты середины отрезка AB , если A (–2; 3), B (6; –3).

2. Найдите длину отрезка EH , если E (–3; 8), H (2; –4).

3. Какая фигура состоит из множества всех точек плоскости, каждая из которых равноудалена от двух данных точек?

4. Принадлежит ли точка A (–6; 2) графику функции y = – 0,5 x ?

5. Функция задана уравнением y = 2 x – 3. Какая линия служит графиком этой функции?

6. На окружности радиуса 7 см даны точки А и В , расстояние между которыми равно 13 см. Л ежит ли центр окружности на прямой АВ ?

7. Вершины треугольника ABC имеют следующие координаты: А (8; –3); В (5; 1); С (12; 0). Докажите, что B = C .

1. Найдите координаты середины отрезка CD , если C (3; –4), D (–3; 6).

2. Найдите длину отрезка KB , если K (–6; –3), B (2; 3).

3. Прямая l является серединным перпендикуляром к основанию AB треугольника ABC и проходит через вершину C . Определите вид треугольника ABC .

4. Принадлежит ли точка В (2; –8) графику функции y = – 4 x ?

5. Функция задана уравнением y = 5 – x . Какая линия служит графиком этой функции?

6. Какой фигурой является множество точек, равноудаленных от данной точки?

7. Вершины четырехугольника ABCD имеют следующие координаты: А (–3; –1); В (1; 2); С (5; –1), D (1; –4). Докажите, что этот четырехугольник – ромб.

Решить задачи № 959 (г), 968, 960 (б).

Решить задачи № 959(в), 967, 960 (в).

1. Лежит ли точка А (2; –1) на окружности, заданной уравнением
( х – 2) 2 + ( у – 3) 2 = 25?

2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 3.

3. Напишите уравнение прямой, проходящей через точку М (3; –2) и параллельной оси ординат.

4. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (–2; 3).

5. Напишите уравнение прямой, проходящей через две точки М (–2; –1) и N (3; 1).

6. Найдите длину вектора (–12; 5).

7. Найдите координаты середины отрезка PQ , если P (5; –3); Q (3; –7).

8. Найдите координаты вектора , если А (2; –5), В (–3; 4).

1. Лежит ли точка А (2; –1) на прямой, заданной уравнением
2 х – 3 у – 7 = 0?

2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 2.

3. Напишите уравнение прямой, проходящей через точку N (–2; 3) и параллельной оси абсцисс.

4. Напишите уравнение прямой, проходящей через начало координат и точку D (3; –2).

5. Напишите уравнение окружности с центром в точке Р (–2; –1), если она проходит через точку Q (1; 3).

6. Найдите расстояние между точками А (–1; 3) и В (2; –1).

7. Найдите координаты вектора , равного сумме векторов и , если (–12; 5), (7; –3).

8. Найдите координаты вектора , если С (–1; 6), D (3; –2).

Устный опрос по теме «Метод координат»

1. Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам.

2. Выведите формулы координат середины отрезка по координатам его концов.

3. Напишите уравнение окружности с центром в точке В (4; 0), если она проходит через точку А (7; 4).

1. Сформулируйте правило нахождения координат разности двух векторов.

2. Выведите формулу для вычисления длины вектора по его координатам.

3. Напишите уравнение прямой, проходящей через две точки А (–3; –3) и В (3; 5).

1. Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам вектора.

2. Выведите уравнение окружности данного радиуса с центром в данной точке, заданной координатами.

3. Найдите координаты середины отрезка АВ , если даны координаты его концов А (–3; 4) и В (3; –6).

1. Сформулируйте утверждение о разложении произвольного вектора по координатным векторам.

2. Выведите уравнение прямой l в прямоугольной системе координат, если l является серединным перпендикуляром к отрезку с концами А ( х 1 ; у 1 ) и В ( х 2 ; у 2 ).

3. Найдите расстояние между точками М (2; –1) и N (5; –3).

КОНТРОЛЬНАЯ РАБОТА № 1

1. Точки E и F лежат соответственно на сторонах AD и BC параллелограмма ABCD ; AE = ED , BF : FC = 4 : 3. Выразите вектор через векторы и .

2. Найдите координаты вектора , если , (3; –2),
( –6; 2).

3. Боковые стороны прямоугольной трапеции равны 15 см и 17 см, средняя линия равна 6 см. Найдите основания трапеции.

1. Точки K и M лежат соответственно на сторонах AB и CD параллелограмма ABCD ; AK = KB , CM : MD = 2 : 5. Выразите вектор через векторы и .

2. Найдите координаты вектора , если , (–3; 6),
(2; –2).

3. Один из углов прямоугольной трапеции равен 120°, бóльшая боковая сторона равна 20 см, средняя линия равна 7 см. Найдите основания трапеции.

1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найти синус, косинус и тангенс меньшего острого угла этого треугольника.

2. Катет прямоугольного треугольника равен 6 дм, а противолежащий угол равен 30°. Найдите гипотенузу этого треугольника.

3. Вычисляя синус острого угла, ученик получил число 1,05. Верны ли его вычисления?

4. Найти косинус острого угла, если его синус равен .

5. Найти тангенс острого угла, если его синус равен .

6. Синус острого угла прямоугольного треугольника равен . Ч ему равен косинус второго острого угла этого треугольника?

1. Стороны прямоугольного треугольника равны 10 дм, 8 дм и 6 дм. Найти синус, косинус и тангенс большего острого угла этого треугольника.

2. Катет прямоугольного треугольника равен 8 см, а противолежащий угол равен 45°. Найти гипотенузу этого треугольника.

3. Вычисляя косинус острого угла прямоугольного треугольника, ученик получил число 1,05. Верны ли его вычисления?

4. Найти синус острого угла, если его косинус равен .

5. Найти тангенс острого угла, если его косинус равен .

6. Косинус острого угла прямоугольного треугольника равен . Ч ему равен синус второго острого угла этого треугольника?

Решить задачи №№ 1015 (а), 1017 (б), 1018 (а), 1019 (а).

Решить задачи №№ 1015 (в), 1017 (а), 1018 (д), 1019 (б).

1. Найдите площадь треугольника, если его основание равно 7 см, а высота равна 4 см.

2. Найдите синус угла, если его косинус равен .

3. Найдите синус угла, если синус смежного с ним угла равен 0,3.

4. Начертите треугольник АВС с тупым углом С . Проведите высоту треугольника из вершины В .

5. Луч ОС образует с положительной полуосью абсцисс угол 60°. Найдите координаты точки С , если ОС = 6 дм.

6. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 43° и 48°.

7. Точка С единичной полуокружности имеет координаты . Найдите угол, который образует луч ОС с положительной полуосью ОХ .

1. Найдите площадь треугольника, если его основание равно 10 дм, а высота равна 5 дм.

2. Найдите косинус угла, если его синус равен .

3. Найдите синус угла, если синус смежного с ним угла равен 0,7.

4. Начертите треугольник СDЕ с тупым углом Е . Проведите высоту треугольника из вершины С .

5. Луч ОВ образует с положительной полуосью абсцисс угол 30°. Найдите координаты точки В , если ОВ = 8 дм.

6. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 35° и 56°.

7. Точка А единичной полуокружности имеет координаты . Н айдите угол, который образует луч ОА с положительной полуосью ОХ .

Решить задачи №№ 1060 (а); 1058 (б); 1061 (а).

Решить задачи №№ 1060 (б); 1058 (а); 1061 (б).

1. Диагонали параллелограмма АВСD пересекаются в точке О . К акие векторы коллинеарны вектору ?

2. Диагонали параллелограмма АВСD пересекаются в точке О . Какие векторы сонаправлены с вектором ?

3. Диагонали параллелограмма АВСD пересекаются в точке О . Какие векторы равны вектору ?

4. При каком условии ?

5. Известно, что = 3, = 4. Найдите , если АОВD – прямоугольник.

6. В треугольнике СDЕ DЕ = 5, СЕ = 4, угол С = 45°. Найдите сторону DЕ .

7. В треугольнике КLM КL = LМ = 5, КМ = 6 . Найдите косинус угла L .

8. В треугольнике ОРQ угол О = 60°, угол Р = 75°, ОР = 8. Найдите сторону РQ .

1. Диагонали ромба КLМР пересекаются в точке Т . Какие векторы коллинеарны вектору ?

2. Диагонали ромба КLМР пересекаются в точке Т . К акие векторы сонаправлены с вектором ?

3. Диагонали ромба КLМР пересекаются в точке Т . Какие векторы равны вектору ?

4. При каком условии ?

5. Известно, что точки С и D лежат соответственно на осях ОХ и ОY прямоугольной системы координат. Найдите , если = 5, = 12.

6. В треугольнике АВС АВ = ВС = 8 , АС = 4. Найдите косинус угла А .

7. В треугольнике ВСD ВС = 6, угол В = 75°, угол С = 45°. Найдите сторону ВD .

8. В треугольнике DЕF DЕ = 6, ЕF = 7, угол Е = 30°. Найдите сторону DF .

1. Известно, что , где и – координатные векторы. Выпишите координаты вектора .

2. Дан вектор (0; 5). Запишите разложение вектора по координатным векторам и .

3. Даны векторы (–1; 2) и (2; 1). Найдите координаты суммы векторов и .

4. Найдите координаты вектора , если (–3; 0).

5. Даны векторы (5; 6) и (–2; 3). Найдите координаты вектора .

6. Две стороны треугольника равны 7 и 3 см, а угол между ними равен 120°. Найдите третью сторону треугольника.

7. В треугольнике АВС угол А = 45°, АВ = 2, АС = 3. Вычислите .

8. Скалярное произведение ненулевых векторов и равно нулю. Чему равен угол между векторами и ?

1. Дан вектор (3; 0). Запишите разложение вектора по координатным векторам и .

2. Известно, что , где и – координатные векторы. Выпишите координаты вектора .

3. Найдите координаты вектора – , если (0; –2).

4. Даны векторы (2; –1) и (3; –1). Найдите координаты разности векторов и .

5. Даны векторы (–1; 9) и (3; –2). Найдите координаты вектора .

6. В треугольнике МРQ угол M = 135°; МР = 5, МQ = 2 . Вычислите .

7. Две стороны треугольника равны 3 и 9 м, а угол между ними равен 60°. Найдите третью сторону треугольника.

8. Чему равно скалярное произведение координатных векторов и ?

1. Вычислите скалярное произведение векторов и , если , а угол между ними равен 120°.

2. Скалярное произведение ненулевых векторов и равно 0. Определите угол между векторами и .

3. Вычислите скалярное произведение векторов и , если (3; –2), (–2; 3).

4. Найдите угол между ненулевыми векторами ( х ; у ) и (– у ; х ).

5. Вычислите косинус угла между векторами и , если (3; –4), (15; 8).

6. Даны векторы (2; –3) и ( х ; –4). При каком значении х эти векторы перпендикулярны?

1. Вычислите скалярное произведение векторов и , если , а угол между ними равен 135°.

2. Скалярное произведение ненулевых векторов и равно нулю. Определите угол между этими векторами.

3. Вычислите скалярное произведение векторов и , если (–4; 5), (–5; 4).

4. Найдите угол между ненулевыми векторами ( х ; – у ) и ( у ; х ).

5. Вычислите косинус угла между векторами и , если (–12; 5), (3; 4).

6. Даны векторы (3; у ) и (2; –6). При каком значении у эти векторы перпендикулярны?

Устный опрос по теме «соотношения межу сторонами и углами треугольника»

1. Что называется тангенсом угла ? Для какого значения тангенс не существует и почему?

2. Сформулируйте и докажите теорему синусов.

3. Даны векторы ( х ; –4) и (2; 3). Найдите значение х , если .

1. Напишите формулы приведения.

2. Сформулируйте и докажите теорему косинусов.

3. Найдите скалярное произведение векторов (–5; 7) и (2; 1).

1. Что такое скалярное произведение векторов?

2. Сформулируйте и докажите теорему о вычислении площади треугольника по двум сторонам и углу между ними.

3. Найдите косинус угла А треугольника АВС , если АВ = 8 см, АС = 6 см, ВС = 12 см.

1. Какие два вектора называются перпендикулярными?

2. Выведите формулу, выражающую косинус угла между ненулевыми векторами через их координаты.

3. Найдите синус угла В треугольника АВС , если АВ = 5 см, АС = 8 см, С = 30°.

КОНТРОЛЬНАЯ РАБОТА № 2

1. Найдите угол между лучом ОА и положительной полуосью ОХ , если А (–1; 3).

2. Решите треугольник АВС , если угол В = 30°, угол С = 105°, ВС =
= 3 см.

3. Найдите косинус угла М треугольника KLМ , если К (1; 7), L (–2; 4), М (2; 0). Найдите косинусы углов K и L .

1. Найдите угол между лучом ОВ и положительной полуосью ОХ , если В (3; 3).

2. Решите треугольник ВСD , если угол В = 45°; угол D = 60°, ВС =
= см.

3. Найдите косинусы углов А , В и С треугольника АВС , если А (3; 9), В (0; 6), С (4; 2).

1. Задачи №№ 1081 (б), 1083 (б), 1084 (г).

2. Докажите, что три вершины правильного шестиугольника, взятые через одну, служат вершинами правильного треугольника.

1. Задачи №№ 1081 (г), 1083 (а), 1084 (е).

2. Докажите, что четыре вершины правильного восьмиугольника, взятые через одну, служат вершинами квадрата.

1. Найдите угол правильного десятиугольника.

2. Найдите сторону правильного треугольника, если радиус описанной около него окружности равен 2 м.

3. Найдите радиус окружности, вписанной в правильный треугольник, если радиус описанной около него окружности равен 2 м.

4. Найдите площадь правильного треугольника, если расстояние от его центра до вершины равно 2 м.

5. Закончите предложение: «Угол с вершиной в центре окружности называется …»

6. Угол с вершиной в центре правильного многоугольника и сторонами, проходящими через две его соседние вершины, равен 36°. Сколько сторон имеет этот многоугольник?

7. Чему равен cos 0°?

8. С помощью циркуля и линейки постройте правильный шестиугольник.

1. Сколько сторон имеет правильный многоугольник, если его сторона стягивает дугу описанной окружности, равную 18°?

2. Найдите площадь квадрата, если радиус описанной около него окружности равен 2 дм.

3. Закончите предложение: «Кругом называется часть плоскости …»

4. Найдите сторону квадрата, если расстояние от его центра до вершины равно 2 дм.

5. Найдите радиус окружности, вписанной в квадрат, если радиус описанной около него окружности равен 2 дм.

6. Чему равен cos 0°?

7. Найдите угол правильного девятиугольника.

8. С помощью циркуля и линейки постройте правильный треугольник.

Решить задачи №№ 1102 (в), 1115 (б), 1109 (в), 1104 (б).

Решить задачи №№ 1102 (г), 1115 (а), 1109 (г), 1116 (а).

1. Площадь круга равна S . Найдите длину ограничивающей его окружности.

2. Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 120°.

3. Длина дуги окружности равна 3π, а ее радиус равен 8. Найдите градусную меру этой дуги.

4. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

5. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45°.

6. Площадь кругового сектора равна 18π м 2 , а его центральный угол равен 40°. Найдите радиус сектора.

1. Длина окружности равна С . Найдите площадь ограниченного ею круга.

2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 и 24 см.

3. Найдите площадь кругового сектора радиуса 3 см, если его центральный угол равен 20°.

4. Площадь кругового сектора равна 10π м 2 , а его радиус равен 6 м. Найдите центральный угол сектора.

5. Найдите длину дуги окружности радиуса 6 дм, если ее градусная мера равна 120°.

6. Найдите радиус окружности, если длина дуги окружности равна 6π, а ее градусная мера равна 60°.

Решить задачи №№ 1125, 1129 (в), 1132 (а), 1134 (а).

Решить задачи №№ 1128, 1129 (г), 1132 (б), 1134 (б).

КОНТРОЛЬНАЯ РАБОТА № 3

1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

2. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 дм 2 .

3. Найдите длину дуги окружности радиуса 3 см, если ее градусная мера равна 150°.

1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 м. Найдите сторону квадрата, вписанного в ту же окружность.

2. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см 2 .

3. Найдите площадь кругового сектора, если градусная мера его дуги равна 120°, а радиус круга равен 12 см.

1) Даны треугольник МNK и точка О . Постройте фигуру F , на которую отображается треугольник MNK при центральной симметрии с центром О .

2) Даны прямая l и четырехугольник РМЕС . Постройте фигуру F , на которую отображается данный четырехугольник при осевой симметрии с осью l .

3) Даны окружность с центром О и прямая l . Постройте фигуру F , на которую отображается данная окружность при осевой симметрии с осью l .

1. В трапеции АВСD боковые стороны АВ и СD равны.

1) Постройте отрезок СА 1 , на который отображается сторона АВ при параллельном переносе на вектор .

2) Найдите площадь треугольника А 1 СD , если АD = 10 см, ВС = 4 см, АВ = 6 см.

2. Докажите, что правильный шестиугольник при повороте на 60° вокруг своего центра отображается на себя.

1. Точка М – середина стороны АС треугольника АВС .

1) Постройте отрезок МВ 1 , на который отображается сторона АВ при параллельном переносе на вектор .

2) Найдите периметр треугольника МDС , где D – точка пересечения отрезков ВС и МВ 1 , если периметр треугольника АВС равен 12 м.

2. Докажите, что правильный пятиугольник при повороте на 72° вокруг своего центра отображается на себя.

Устный опрос по теме «Движения»

1. Объясните, что такое отображение плоскости на себя.

2. Докажите, что параллельный перенос является движением.

3. Точка М – середина стороны ВС правильного треугольника АВС , точки N и K симметричны точке М относительно прямых АВ и АС . Докажите, что NK АМ .

1. Что такое движение плоскости?

2. Докажите, что осевая симметрия является отображением плоскости на себя.

3. На окружности с центром О и радиусом r отмечена точка А . Постройте окружность, на которую отображается данная окружность при повороте вокруг точки А на 60° по часовой стрелке. Н айдите длину отрезка, соединяющего точки пересечения данной и построенной окружностей.

1. На какую фигуру отображается при движении отрезок?

2. Докажите, что центральная симметрия является движением.

3. Дан равнобедренный треугольник АВС с основанием ВС . Постройте точки D и Е , на которые отображаются точки А и С при параллельном переносе на вектор , и докажите, что АЕ = DВ .

1. На какую фигуру отображается при движении треугольник?

2. Докажите, что поворот плоскости вокруг точки является движением.

3. Точка пересечения диагоналей четырехугольника АВСD является его центром симметрии. Докажите, что АВСD – параллелограмм.

КОНТРОЛЬНАЯ РАБОТА № 4

1. Дана трапеция АВСD . Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ .

2. Две окружности с центрами О 1 и О 2 , радиусы которых равны, пересекаются в точках М и N . Через точку М проведена прямая, параллельная О 1 О 2 и пересекающая окружность с центром О 2 в точке D . И спользуя параллельный перенос, докажите, что четырехугольник О 1 МDО 2 является параллелограммом.

1. Дана трапеция АВСD . Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны СD .

2. Дан шестиугольник А 1 А 2 А 3 А 4 А 5 А 6 . Его стороны А 1 А 2 и А 4 А 5 , А 2 А 3 и А 5 А 6 , А 3 А 4 и А 6 А 1 попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали А 1 А 4 , А 2 А 5 , А 3 А 6 данного шестиугольника пересекаются в одной точке.

Материал для итогового повторения

Основные вопросы программы: равенство и подобие треугольников, сумма углов треугольника, равнобедренный треугольник, прямоугольный треугольник, площадь треугольника.

1. В треугольниках АВС и DЕK АВ = DЕ , АС = DK , ВР = ЕМ , где Р и М – середины сторон АС и DK .

1) Докажите, что треугольник АВС равен треугольнику DЕK .

2) Найдите S АВС , если ЕМ = 3 см, DK = 4 см, ЕМK = 135°.

2. В треугольниках АВС и А 1 В 1 С 1 АС = А 1 С 1 , ВС = В 1 С 1 , ВD = В 1 D 1 , где ВD и В 1 D 1 – высоты треугольников, причем точки D и D 1 лежат на отрезках АС и А 1 С 1 .

1) Докажите, что треугольник АВС равен треугольнику А 1 В 1 С 1 .

2) Найдите радиус окружности, описанной около треугольника В 1 D 1 С 1 , если известно, что ВD = 6 см, DС = 8 см.

3) Найдите угол А 1 С 1 В 1 , если ВD = 6 см, DС = 8 см.

3. На рисунке дан прямоугольный треугольник АВС с гипотенузой АВ , DЕ АВ .

1) Докажите, что треугольник АВС и треугольник DАЕ подобны.

2) Найдите катеты треугольника АВС , если АВ = 13 см, АЕ = 5,2 см, DЕ = 2 см.

3) Докажите, что около четырехугольника ВDЕС можно описать окружность.

4. В прямоугольном треугольнике АВС проведена высота СD к гипотенузе АВ , СD = а , АD = b .

Н айдите: 1) ВС ; 2) радиус окружности, вписанной в треугольник АВС ; 3) отношение площадей треугольников АDС и АСВ .

5. В треугольнике АВС АВ = 14 см, АС = 15 см, ВС = 13 см.

Н айдите: 1) длину меньшей высоты треугольника; 2) площадь треугольника АDС , если АD – биссектриса треугольника АВС ; 3) медиану АЕ треугольника АВС .

6. С помощью циркуля и линейки постройте треугольник АВС по сторонам АВ и АС и высоте, проведенной к АС .

7. Площадь треугольника АВС равна Q . Найдите площадь треугольника АОВ 1 , где О – точка пересечения медиан треугольника АВС , а В 1 – середина стороны АС .

8. С помощью циркуля и линейки постройте равнобедренный треугольник АВС по основанию АС и углу В и биссектрису ВD внешнего угла этого треугольника при вершине В .

Основные вопросы программы: окружность и круг, касательная к окружности и ее свойства; окружность, описанная около треугольника; окружность, вписанная в треугольник.

1. Хорда АВ окружности радиуса 4 см видна из центра под углом 90°.

Найдите: 1) хорду АВ и расстояние от центра окружности до этой хорды; 2) углы треугольника АВС , где С – точка, расположенная на большой дуге АВ окружности так, что АС : СВ = 5 : 4; 3) хорду ВС .

2. Две взаимно перпендикулярные хорды АВ и СD окружности пересекаются в точке K , причем АK = 6 см, ВK = 32 см, KD = 24 см.

Найдите: 1) хорды ВD и СD ; 2) расстояние от точки А до прямой ВD ; 3) радиус данной окружности.

3. Треугольник АВС с углом В , равным 135°, вписан в окружность с центром О и радиусом R = 10 см.

Найдите: 1) сторону АВ ; 2) сторону АВ и S АВС , если известно, что угол АСВ равен 30°.

4. Точки М , D и K лежат на окружности, угол DМK равен 45°, хорда DK = 12 см.

Найдите: 1) радиус данной окружности; 2) угол МКD , если известно, что DМ = 6 см.

5. Радиус окружности, вписанной в равнобедренный треугольник АВС с основанием АС , равен 3 см, KВ = 4 см, где K – точка касания окружности с боковой стороной.

Найдите: 1) сторону АС ; 2) угол ВАС ; 3) радиус окружности, описанной около треугольника АВС .

6. В равнобедренный треугольник АВС с основанием АС вписана окружность, касающаяся сторон АВ и ВС в точках М и Н .

1) Докажите, что треугольник МВН треугольнику АВС .

2) Найдите угол ВАС и радиус окружности, если АВ = 2 м, МН = 1 м.

Основные вопросы программы: параллелограмм и его свойства; признаки параллелограмма; прямоугольник, ромб, квадрат и их свойства; трапеция, многоугольник, правильные многоугольники.

1. На рисунке 1 АЕFС – прямоугольник; АС = 10 см, АЕ = 3 см,
ВМ = АМ .

1) Докажите, что МN – средняя линия треугольника АВС .

2) Найдите S АМNС . 3) Найдите S АВС .

Рис. 1 Рис. 2 Рис. 3

2. В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке Е ; АВ = а ; АD = b . Найдите: 1) отрезки ВЕ и ЕС ; 2) отрезки ВK и KD и S АВЕ , если K – точка пересечения АЕ и ВD , а угол А равен 60°.

3. На рисунке 2 АВСD – параллелограмм, угол 1 равен углу 2.

1) Докажите, что четырехугольник ВFDK – параллелограмм, и найдите его площадь и периметр, если KF = 10 см, ВD = 6 см, KОD = 150°. 2) Каким условиям должны удовлетворять отрезки KF и ВD , чтобы параллелограмм ВFDK был прямоугольником (ромбом, квадратом)?

4. Меньшая диагональ параллелограмма перпендикулярна к его стороне, а высота, проведенная из вершины тупого угла, делит большую сторону на отрезки, равные 9 см и 16 см.

Н айдите: 1) стороны и высоту параллелограмма, проведенную из вершины тупого угла; 2) диагонали параллелограмма; 3) площадь параллелограмма.

5. В параллелограмме АВСD проведена биссектриса АK угла А , точка K делит сторону ВС на отрезки ВK = 4 см и KС = 2 см. Расстояние между параллельными прямыми АD и ВС равно 2 см.

Найдите: 1) углы параллелограмма; 2) площадь треугольника АВС ; 3) радиус окружности, описанной около треугольника DКС .

6. На рисунке 3 точки М , N , Р и Q – середины сторон четырехугольника АВСD , АС = 10 см, ВD = 18 см.

1) Докажите, что MNPQ – параллелограмм, и найдите его периметр. 2) Найдите площади четырехугольников АВСD и MNPQ , если угол ВОС равен 60°.

7. В равнобедренную трапецию, основания которой равны 2 см и 8 см, вписана окружность.

Найдите: 1) боковую сторону трапеции; 2) радиус вписанной окружности; 3) площадь трапеции.

8. В равнобедренной трапеции с основаниями АD и ВС угол D равен 60°, ВС = 12 см, а угол ВСА равен 30°.

1) Докажите, что треугольник АВС равнобедренный. 2) Найдите радиус окружности, описанной около треугольника АСD . 3) Найдите площадь трапеции АВСD .

9. В ромб, сторона которого равна диагонали и равна а , вписана окружность, а в эту окружность вписан правильный треугольник.

Найдите: 1) радиус окружности; 2) сторону треугольника; 3) площади ромба, круга и правильного треугольника.

10. Каждый угол правильного п -угольника А 1 А 2 … А п равен 150°.

1) Найдите число сторон этого многоугольника. 2) Найдите А 2 А 3 А 10 . 3) Докажите, что треугольник А 1 А 3 В подобен треугольнику А 6 А 10 В , где В – точка пересечения диагоналей А 1 А 6 и А 3 А 10 этого многоугольника.

11. Внешний угол правильного п -угольника А 1 А 2 … А п в три раза меньше угла этого многоугольника.

1) Найдите число сторон этого многоугольника. 2) Найдите А 3 А 1 А 6 . 3) Докажите, что четырехугольник А 1 А 3 А 4 А 8 – равнобедренная трапеция.

ВЕКТОРЫ. МЕТОД КООРДИНАТ. ДВИЖЕНИЯ

Основные вопросы программы: вектор, длина вектора, сложение векторов и его свойства, умножение вектора на число и его свойства, коллинеарные векторы, прямоугольные координаты точек на плоскости, формула расстояния между двумя точками плоскости с заданными координатами, координаты середины отрезка, уравнения окружности и прямой, применение векторов и метода координат к доказательству теорем и решению задач. Движения.

1. Четырехугольник АВСD задан координатами своих вершин: А (–3; –2), В (–1; 2), С (2; 2), D (4; –2).

1) Найдите координаты середин сторон этого четырехугольника.

2) Докажите, что середины сторон четырехугольника АВСD являются вершинами ромба, и найдите площадь этого ромба.

2. Дан четырехугольник АВСD .

1) Определите вид четырехугольника АВСD , если , и выразите вектор через векторы и .

2) Выразите векторы через векторы и , если М , N , Р и Q – середины сторон АВ , ВС , СD и АD .

3) Определите вид четырехугольника МNPQ .

3. Дан правильный шестиугольник АВСDЕF со стороной а . Найдите скалярное произведение векторов: 1) ; 2) ; 3) ; 4) .

4. Найдите косинусы углов треугольника АВС , если А (1; 3), В (8; 2), С (5; –1).

5. В параллелограмме АВСD диагональ ВD равна стороне ВС , точка М – середина стороны ВС , отрезок DМ перпендикулярен к диагонали АС . Найдите углы параллелограмма.

6. Две окружности радиуса r с центрами О 1 и О 2 касаются друг друга в точке М . На первой окружности отмечена точка А , а на второй – точка В так, что хорды АМ и ВМ взаимно перпендикулярны. Докажите, что: 1) при параллельном переносе на вектор отрезок АС отображается на отрезок ВМ ; 2) АВ = 2 r .

7. На сторонах правильного треугольника построены квадраты. Докажите, что центры этих квадратов являются вершинами правильного треугольника.

Видео:1 задание ЕГЭ 2023 по профильной математике. РЕШЕНИЕ.В треугольнике ABC угол C равен 90°, AC = 4,8,Скачать

По теме: методические разработки, презентации и конспекты

Cистема КИМов и дидактических материалов — необходимый инструментарий оценки качества знаний(из опыта работы)

На современном этапе развития общества возросла потребность в подготовке школьника к тем условиям, в которых он будет жить. Новая концепция образования требует таких методов и приемов обучения, .

Тестирование, как инструментарий мониторинга качества знаний учащихся

Предложены тесты для контроля уровня знаний учащихся по математике. Тесты составлены таким образом, чтобы учащиеся могли видеть результат образовательного процесса. Визуализация итогов тестирова.

Инструментарий для оценивания знаний 7 класс

Содержит самостоятельные работы, математиечские диктанты. тематические зачёты. УМК Дорофеев В.Г.

Инструментарий для оценивания знаний 8 класс

Подборка самостоятельных работ, математических диктантов, тематических зачётов, тоговых контрольных работ для 8 класс УМК Дорофеев В.Г.

Инструментарий для оценивания знаний 9 класс

Инструментарий для оценивания знаний 9 класс УМК Дорофеев В.Г.

Инструментарий для оценивания знаний 8 класс

Инструментарий для оценивания знаний 8 класс УМК Атанасян Л.С.

Диагностический инструментарий. Система оценивания ключевых компетенций учащихся.

Анкета позволяет оценить уровень сформированности информационной компетенции учащихся.

Видео:В треугольнике ABC угол C=90°, СН — высота, BC = 3, косинус A = корень из 35/6. Найдите АН.Скачать

В треугольнике abc угол c 90 ac 3 см bc 4 см постройте вектор

В треугольнике ABC угол C равен 90°. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.

Приведем решение Айши Гучиговой.

Найдем гипотенузу треугольника:

Площадь треугольника ABC равна С другой стороны, откуда

Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

В треугольнике авс угол с=90°, ас=3 см, вс=4 см. постройте вектор q=2/3 ca+2cв-0,2ав. .

Видео:В треугольнике ABC AC=4, BC=3, угол C равен 90° ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Ответы

эля я у тебя походу оставила листок с

в одну коробку вмещается х 7х=3х+32 4х=32 х=8

2)32: 4=8 карандашей-в одной коробке.

m(спирта) = v(спирта)*ρ(спирта) = 40*0,807 =32,28 г — с примесями m(спирта) = 32,28*(100%-6%)/100% =30,34 г — без примесей

n(спирта) = m/m = 30.34/46 =0.66 моль

уравнение: c2h5oh = c2h4 + h2o

по уравнению n (c2h4) =n(спирта)= 0,66 моль

v (c2h4)теорет = 0,66*22,4 = 14,78 л

φ = v (c2h4)практ/v (c2h4)теорет = 10,2/14,78*100% = 69% наверное

периметр квадрата 28 см

периметр прямоугольника 28 см

периметр квадрата и прямоугольника равны

площадь квадрата 49см в квадрате

площадь прямоугольника 48см в квадрате

49-48=1(см) площадь квадрата больше на 1 см квадратный

🎥 Видео

Геометрия В треугольнике ABC известно, что угол C = 90, AC = BC = 14 см. Две стороны квадрата CDEFСкачать

Геометрия В треугольнике ABC известно, что угол C = 90, AC = BC = 6 см. Прямоугольник CMKN построенСкачать

№745. В прямоугольнике ABCD AB=3см, BC=4см, M-середина стороны AB.Скачать

В треугольнике ABC угол C равен 90°, AC = 2, синус A = корень из 17/17 . Найдите BC.Скачать

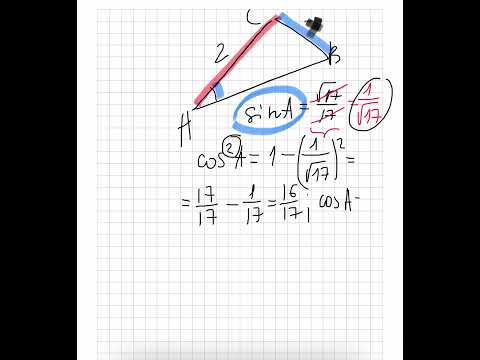
В треугольнике ABC угол C равен 90°, CH – высота, AB = 13, тангенс A =1/5. Найдите AH.Скачать

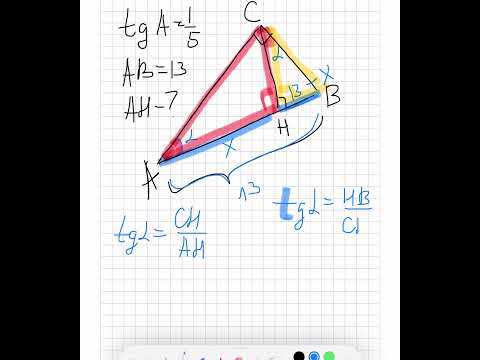
Геометрия. ОГЭ по математике. Задание 15Скачать

3 урок. Произведение вектора на число. Средняя линия трапеции | Геометрия. 9 классСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

🔴 В треугольнике ABC угол C равен 90°, AB=15, AC=9 ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

В треугольнике ABC угол C равен 90°, AB = 13, тангенс A = 1/5. Найдите высоту CH.Скачать

№90. Сторона AB треугольника ABC равна 17см, сторона АС вдвое больше стороны AB, а сторона ВССкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать