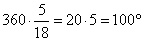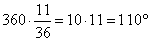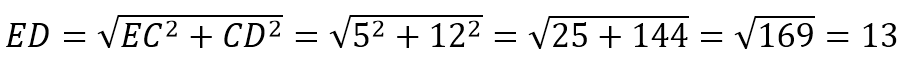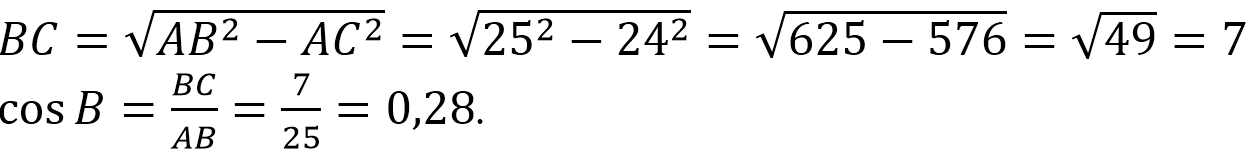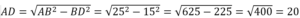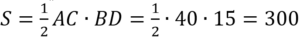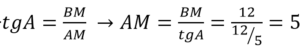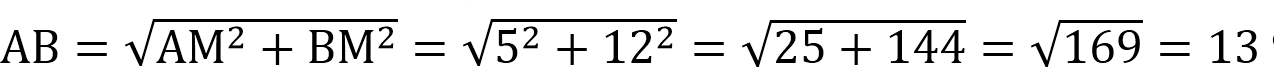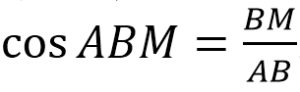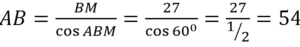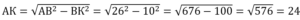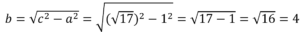Ав 20 вс 15 длина окружности

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Онлайн калькулятор

Как посчитать длину окружности зная диаметр

Какая длина у окружности если

Какова длина окружности (С) если её диаметр d?

Формула

С = π⋅d , где π ≈ 3.14

Пример

Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная радиус

Какая длина у окружности если

Какова длина окружности (С) если её радиус r?

Формула

С = 2⋅π⋅r , где π ≈ 3.14

Пример

Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная её площадь

Какая длина у окружности если

Какова длина окружности (С) если её площадь S?

Формула

С = 2π⋅ √ S /_π , где π ≈ 3.14

Пример

Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Задание №15 ЕГЭ по математике базового уровня

Видео:Длина окружности. Математика 6 класс.Скачать

Планиметрия

В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.

Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня

Вариант 15МБ1

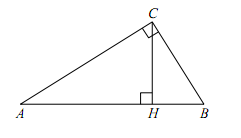
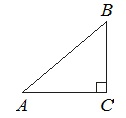
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.

Алгоритм выполнения:

1. Вспомнить определение косинуса угла.
2. Записать выражение для нахождения косинуса угла.
3. Выразить неизвестную величину.
4. Вычислить.

Решение:

Вспомним определение косинуса угла.

Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.

Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.

Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.

Прилежащий к углу А катет – АН.

Получим cos A = АН/АС.

Выразим неизвестную величину.

АН = АС · cos A = 4 · 0,8 = 3,2

Вариант 15МБ2

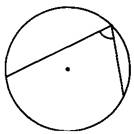
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 5/18 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ3

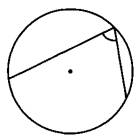
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 11/36 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ4

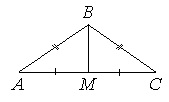
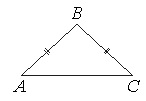
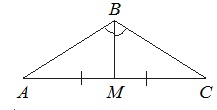
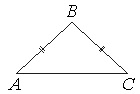
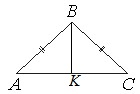
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.

Алгоритм выполнения

1. Определяем вид треугольника.
2. Доказываем, что медиана ВМ является и высотой.
3. Из прямоугольного треугольника АМВ по т.Пифагора находим медиану ВМ.

Решение:

Если АВ=ВС, то ∆АВС – равнобедренный.

В равнобедр.треугольнике медиана, опущенная на основание, является еще и высотой. Тогда угол АМВ=90 0 , и ∆АМВ – прямоугольный с катетами АМ и ВМ и гипотенузой АВ.

По т.Пифагора АМ 2 +ВМ 2 =АВ 2 . Отсюда: .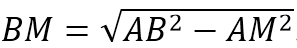

Т.к. АМ медиана, то

.

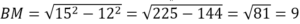
Вариант 15МБ5

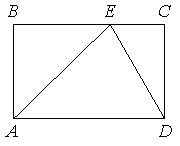
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.

Алгоритм выполнения

1. Находим ЕС.
2. Определяем значение СD.
3. Из прямоугольного треугольника АСD по т.Пифагора находим ЕD.

Решение:

Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.

Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.

Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=90 0 , и ∆ЕСD прямоугольный.

Тогда по т.Пифагора ЕD 2 =ЕC 2 +СD 2 . Получаем:

Вариант 15МБ6

В треугольнике АВС угол С равен 90 0 , АВ=25, АС=24. Найдите cos B.

Алгоритм выполнения

1. По т.Пифагора находим величину катета ВС.
2. По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.

Решение:

Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ 2 =АС 2 +ВС 2 .

Вариант 15МБ7

В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.

Алгоритм выполнения

1. Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB.
2. Из ∆ADB находим катет ВD, используя sin A.
3. Находим АD из ∆ADB по т.Пифагора. Далее определяем АС как 2AD.
4. Находим площадь ∆АВС по формуле S=ah/2.

Решение

В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.

Из ∆ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 →

Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.

Площадь ∆АВС равна:

Вариант 15МБ8

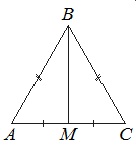
В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.

Алгоритм выполнения

1. Доказываем, что ∆АВМ прямоугольный.
2. Из ∆АВМ, используя формулу-определение для тангенса, находим АМ.
3. Из ∆АВМ по теореме Пифагора находим АВ.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.

Из ∆АВМ по теореме Пифагора АВ 2 =АМ 2 +ВМ 2 →

Вариант 15МБ9

В треугольнике АВС угол В равен 120 0 . Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.

Алгоритм выполнения

1. Определяем величину угла АВМ.
2. Доказываем, что ∆АМВ прямоугольный.
3. Находим АВ, используя формулу-определение для косинуса.

Решение:

По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет

Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.

В прямоугольного ∆АМВ:

Вариант 15МБ10

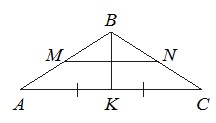
В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.

Алгоритм выполнения

1. Доказываем, что ∆АКВ прямоугольный.
2. Из ∆АКВ по т.Пифагора находим АК.
3. Находим АС как 2АК.
4. Находим МN как среднюю линию.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВК, опущенная на основание АС, является и высотой. Поэтому угол АКВ равен 90 0 , и ∆АКВ прямоугольный.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 .

Поскольку ВК медиана, то АС=2АК=2·24=48.

Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).

Вариант 15МБ11

В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.

Алгоритм выполнения

1. Находим длину отрезков АМ и МС как половину от АС.
2. Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС.
3. Находим АН как сумму АМ и МН.

Решение:

Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.

По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.

Вариант 15МБ12

Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.

Алгоритм выполнения

1. Находим величину 2-го (неизвестного) катета по т.Пифагора.
2. Определяем площадь треугольника как полупроизведение катетов.

Решение:

Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.

По т.Пифагора a 2 +b 2 =c 2 . Отсюда:

Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.

Вариант 15МБ13

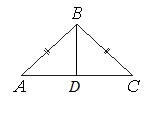
В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.

Алгоритм выполнения

1. Используя формулу для площади треугольника S=ah/2 и зная величину а (по условию – основание АС), найдем высоту ∆АВС. Отображаем высоту на рисунке, обозначив ее пересечение с основанием буквой К.
2. Доказываем, что высота ВК является и его медианой. Отсюда находим АК.
3. Из ∆АКВ по т.Пифагора находим АВ.

Решение:

Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.

Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 . Получаем:

Видео:Длина окружности. Площадь круга.Скачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:Радиус и диаметрСкачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:Длина окружности и площадь кругаСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

🔥 Видео

Длина окружности. Площадь круга, 6 классСкачать

Окружность и круг, 6 классСкачать

Площадь круга. Математика 6 класс.Скачать

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

9 класс, 26 урок, Длина окружностиСкачать

6 класс, 24 урок, Длина окружности и площадь кругаСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

6 класс, 3 урок, Длина окружности и площадь кругаСкачать

МЕРЗЛЯК-6. ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА. ПАРАГРАФ-25Скачать

КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Длина окружности. 9 класс.Скачать

Талантливый ученик решает задачки. Длина окружности. Подробный разбор темыСкачать