Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.
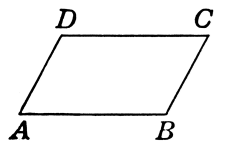
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
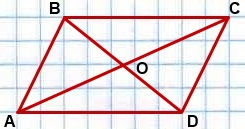
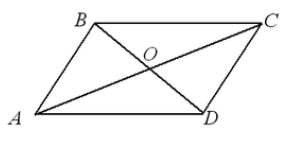
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
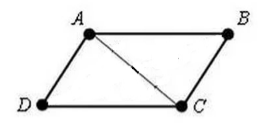
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
Для этого можно доказать равенство одной из тех же пар треугольников.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Параллелограмм и трапеция
Вы будете перенаправлены на Автор24
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Предварительные сведения
Для начала разберемся с таким понятием, как четырехугольник.
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Рассмотрим далее подробно параллелограмм и трапецию.
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Параллелограмм
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
Рисунок 1. Параллелограмм
Параллелограмм имеет два основных свойства. Введем и докажем их.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Пусть нам дан параллелограмм $ABCD$. Проведем в нем диагональ $AC$ (рис. 2).
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
как накрест лежащие углы.
Рассмотрим параллельные прямые $AD$ и $CB$ и их секущую $AC$. Тогда
как накрест лежащие углы.
Следовательно, $angle A=angle C$.
По $II$ признаку равенства треугольников,
так как $AC$ — их общая сторона. Значит
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Пусть нам дан параллелограмм $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 3).
Готовые работы на аналогичную тему
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущие $AC$ и $BD$. Тогда
как накрест лежащие углы.textit
Так как, по свойству $1$, $AB=CD$, то, по II признаку равенства треугольников,
Видео:Параллелограмм. 8 класс.Скачать

Трапеция
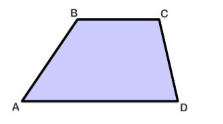
Трапеция — это четырехугольник, в котором две противоположные стороны параллельны между собой, а другие две противоположные стороны не параллельны между собой (рис. 4).
Рисунок 4. Трапеция
При этом параллельные стороны называют основаниями трапеции, а две другие — боковыми сторонами трапеции.
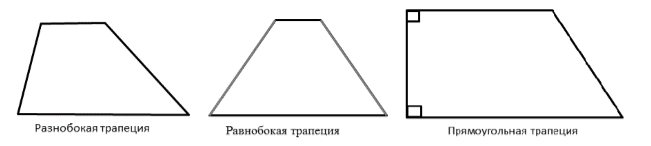
Выделяют следующие виды трапеций.
[Определение] Если у трапеции не параллельные (боковые) стороны равны между собой, то её называют равнобедренной. [/Определение]
Если у трапеции два один угол прямой, то её называют равнобедренной.
В отличных от определений $4$ и $5$ случаях, трапецию называют разнобокой (рис. 5).
Рисунок 5. Виды трапеций
Трапеция обладает следующим свойством.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
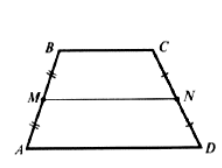
Пусть нам дана трапеция $ABCD$ с основаниями $AD и BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 6).
Рисунок 6. Средняя линия трапеции
Докажем, что $MN||AD и MN=frac$.
Рассмотрим вектор $overrightarrow$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что $overrightarrow=overrightarrow+overrightarrow+overrightarrow$
С другой стороны $overrightarrow=overrightarrow+overrightarrow+overrightarrow$
Сложим два последних равенства, получим
Из этого же равенства (так как $overrightarrow$ и $overrightarrow$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Видео:8 класс, 4 урок, ПараллелограммСкачать

Пример задачи
Боковые стороны трапеции равны $17 см$ и $19 см$ соответственно. Периметр трапеции равен $50 см$. Найти длину средней линии трапеции.
Решение.
Сложим боковые стороны, получим $17 см+19 см=36 см$
Значит, зная периметр равный $50 см$, сумма оснований
[50 см-36 см=14 см]
Следовательно, по теореме $1$, средняя линия равна $frac=7 см$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 16 05 2022
Видео:Признаки параллелограмма Доказательство признаков параллелограммаСкачать

Четырёхугольники: параллелограмм (частные случаи), трапеция
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы рассмотрим различные четырехугольники, а именно частные случаи параллелограмма – прямоугольник, ромб и квадрат; трапецию и ее частные случаи. Кроме того, мы сформулируем теорему Фалеса и решим пример.
📺 Видео
ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Задание 25 Доказать, что четырёхугольник параллелограмм Определение параллелограммаСкачать
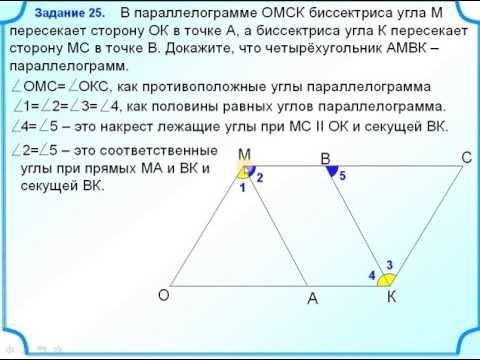
Геометрия Признак параллелограмма: Если в четырехугольнике противолежащие стороны равныСкачать

Геометрия 8 класс (Урок№4 - Трапеция)Скачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Доказательство первого признака параллелограммаСкачать

№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

8 класс, 6 урок, ТрапецияСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Признаки параллелограмма. 8 класс.Скачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать