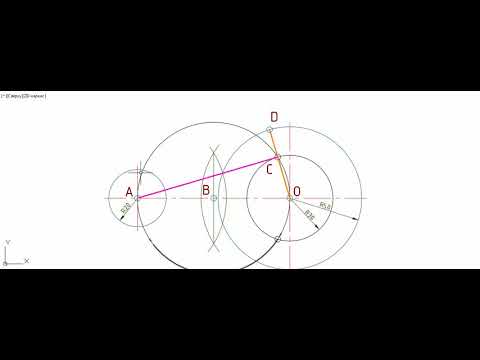
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Касательные к окружностиСкачать  Касание окружностейГоворят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним. Видео:Внутренняя касательная к двум окружностямСкачать  Внутреннее касаниеКасание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом. При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов. Видео:1 2 4 сопряжение окружностейСкачать  Внешнее касаниеКасание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом. При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Общие касательныеВыясним сколько общих касательных имеют две окружности и как эти общие касательные могут быть расположены.
Если две окружности не пересекаются и окружность меньшего радиуса лежит внутри окружности большего радиуса, то они не имеют общих касательных.
В другом случае не пересекающиеся окружности имеют четыре общие касательные.
внешние общие касательные При этом, если обе окружности лежат по одну сторону от касательной (в одной полуплоскости), то такая касательная называется внешней.
внутренние общие касательные Если окружности лежат по разные стороны от общей касательной (в разных полуплоскостях), то такая касательная называется внутренней.
Если две окружности имеют внутреннее касание, то у них есть одна общая касательная.
При внешнем касании две окружности имеют три общие касательные.
Две пересекающиеся окружности имеют две общие касательные. 🎦 ВидеоЕГЭ по математике, c4, две окружностиСкачать  Построение общей внешней касательной к двум окружностямСкачать  Параллельные прямые | Математика | TutorOnlineСкачать  Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать  Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать  Построение касательной к окружностиСкачать  САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать  Окружность и подобные треугольники.Теоремы о секущих, касательных,хордах. Геометрические конструкцииСкачать  Касательные к двум окружностям.Скачать  Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать  ArtCAM, касательные (тангенциальный) линии для двух окружностейСкачать  Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Геометрия. 8 класс. Урок 9 "Касательные к окружности"Скачать  |
