Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
| = | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
| = | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
| = | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
| = |
| = |
| = |
| . |
|---|
| cos(λ1) | = |
| . |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
| = |
| . |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
| = |
| . |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
Видео:№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

Объем параллелепипеда, построенного на векторах онлайн
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Геометрия. 10 класс
Компланарные векторы
Подчеркните верное утверждение:
1) Любые два вектора компланарны.
2) Любые три вектора компланарны.
3) Если три вектора компланарны, то один из них нулевой.
4) Если векторы компланарны, то они коллинеарны.
Компланарные и некомпланарные векторы
компланарные
некомпланарные
Компланарные векторы
Точки А, В и С лежат на окружности, а точка М не лежит в плоскости этой окружности. Тогда векторы $overrightarrow, overrightarrow$ и $overrightarrow$
Компланарные и некомпланарные векторы
Укажите вывод, который следует из данных утверждений
1) Точки А, В и С не лежат на одной прямой, а точка O не лежит в плоскости (АВС). Тогда векторы
$overrightarrow, overrightarrow, overrightarrow$
2) $overrightarrow=xcdot overrightarrow+ycdot overrightarrow$
Тогда векторы $overrightarrow, overrightarrow$, и $overrightarrow$
Компланарные векторы. Векторный метод решения задач
Решите задачу и введите правильный ответ:
Разложение векторов
В параллелепипеде ABCDA1B1C1D1 точка M — середина ребра CC1. Разложите вектор AМ по векторам AB, AD, AA1.
Выберите верное утверждение и выделите его цветом:
Доказательство теоремы
Докажите что векторы $overrightarrow,overrightarrow<A_B_>$ и $overrightarrow$ компланарны.
Восстановите последовательность в доказательстве:
Отложим от точки А вектор $overrightarrow$,равный вектору $overrightarrow$
Выбираем точку А и отложим от неё векторы
Векторы $overrightarrow, overrightarrow$ и $overrightarrow$ лежат в одной плоскости, значит они компланарны.
Отложим от точки А вектор $overrightarrow$,равный вектору $overrightarrow<A_B_>$
Компланарные векторы. Векторный метод решения задач
В параллелепипеде $ABCDA_ B_ C_ D_$, $О$ — точка пересечения диагоналей. Разложите вектор $AО$ по векторам $AB$, $AD$ и $AA_$.
Выберите правильный вариант ответа:
Компланарные векторы. Векторный метод решения задач
DABC – тетраэдр. О – точка пересечения медиан грани BDC. Тогда вектор $overrightarrow$ равен:
Выберите правильный вариант ответа:
Компланарные векторы. Векторный метод решения задач
Восстановите последовательность элементов в доказательстве утверждения поставьте правильную последовательность этапов:
Доказать, что если М – точка пересечения медиан треугольника АВС и О — произвольная точка пространства, то выполняется равенство
Разделим обе части на 3, получим $overrightarrow=frac(overrightarrow+overrightarrow+overrightarrow)$
Так как $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Запишем следующие векторные равенства: $overrightarrow=overrightarrow+overrightarrowoverrightarrow=overrightarrow+overrightarrowoverrightarrow =overrightarrow+overrightarrow$
Сложив эти равенства по частям, получаем: $overrightarrow+overrightarrow+overrightarrow=3overrightarrow+(overrightarrow+overrightarrow+overrightarrow)$
Видео:№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

В параллелепипеде abcda1b1c1d1 заданы векторы совпадающие с его ребрами
4.6. Задачи с решениями
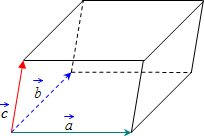
1. В параллелепипеде обозначим . Выразить через векторы a, b, с диагонали параллелепипеда и диагонали граней.
Решение. Сделаем чертёж. Пользуясь правилом сложения векторов, получаем:
AC = AB + AD = b + с, AC1 = AA1 + AC = a + b + с .
Из того же треугольника AA1C получаем: A1C = AC — AA1 = b + с — a.
Чтобы найти B1C, заметим, что B1C = A1D, так как у этих векторов совпадают и длины, и направления. Поэтому B1C = A1D = AD — AA1 = с — a.
Аналогично: DC1 = AB1 = AA1 + AB = a + b .
2. Найти длину и направляющие косинусы вектора AB, если его начало и конец находятся в точках A(7, 6), B(2 — 6).
Решение. Так как каждая точка задана двумя координатами, то рассматривается вектор на плоскости. Находим его координаты, вычитая из координат точки B (конца вектора) координаты точки A (начала вектора): AB = (2 — 7, —6 — 6) = (—5, —12). Находим длину: |AB | = 13, направляющие косинусы: .
3. Найти координату z вектора a = (1, —3, z), если известно, что она отрицательна, а модуль |a| = . Где окажется конец вектора a, если его отложить из точки M(5, —2, 1)?
Решение. По условию, . поэтому ZN = —8.
4. Найти расстояние между точками A(5, —2, 4) и B( —1, 0, 6).
Решение. Расстояние равно длине вектора AB. Найдём:
5. При каких p, q векторы a = (2,p, — 1), b = qi + 9j + 3k будут коллинеарными?
📸 Видео
Правило параллелепипеда для векторовСкачать

10 класс, 44 урок, Правило параллелепипедаСкачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

1. Векторы и параллелограмм задачи №1Скачать

№361. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторыСкачать
№78. На рисунке 42 изображен параллелепипед ABCDA1B1C1D1, на ребрах которого отмечены точки МСкачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

№84. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящейСкачать

№87. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью MNK, где точки М,Скачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

§20 Нахождение объёма параллелипипедаСкачать

№322. На рисунке 104 изображен параллелепипед. Точки М и К — середины реберСкачать

№85. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где КСкачать

№77. Сумма всех ребер параллелепипеда ABCDA1B1C1D1. равна 120 см. Найдите каждое реброСкачать

 Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).