Вы будете перенаправлены на Автор24
Видео:№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
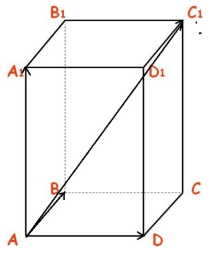
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Видео:№361. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторыСкачать
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow
$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
Доказательство.
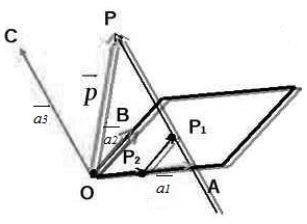
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow
=overrightarrow]
Рассмотрим следующий рисунок:
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow
$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow
$ и $overrightarrow$ коллинеарны, то
Тогда, получаем, что
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow
$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:
Вычтем эти разложения друг из друга
Из этого получаем
Теорема доказана.
Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Геометрия. 10 класс
Компланарные векторы
Подчеркните верное утверждение:
1) Любые два вектора компланарны.
2) Любые три вектора компланарны.
3) Если три вектора компланарны, то один из них нулевой.
4) Если векторы компланарны, то они коллинеарны.
Компланарные и некомпланарные векторы
компланарные
некомпланарные
Компланарные векторы
Точки А, В и С лежат на окружности, а точка М не лежит в плоскости этой окружности. Тогда векторы $overrightarrow, overrightarrow$ и $overrightarrow$
Компланарные и некомпланарные векторы
Укажите вывод, который следует из данных утверждений
1) Точки А, В и С не лежат на одной прямой, а точка O не лежит в плоскости (АВС). Тогда векторы
$overrightarrow, overrightarrow, overrightarrow$
2) $overrightarrow=xcdot overrightarrow+ycdot overrightarrow$
Тогда векторы $overrightarrow, overrightarrow$, и $overrightarrow$
Компланарные векторы. Векторный метод решения задач
Решите задачу и введите правильный ответ:
Разложение векторов
В параллелепипеде ABCDA1B1C1D1 точка M — середина ребра CC1. Разложите вектор AМ по векторам AB, AD, AA1.
Выберите верное утверждение и выделите его цветом:
Доказательство теоремы
Докажите что векторы $overrightarrow,overrightarrow<A_B_>$ и $overrightarrow$ компланарны.
Восстановите последовательность в доказательстве:
Отложим от точки А вектор $overrightarrow$,равный вектору $overrightarrow<A_B_>$
Выбираем точку А и отложим от неё векторы
Векторы $overrightarrow, overrightarrow$ и $overrightarrow$ лежат в одной плоскости, значит они компланарны.
Отложим от точки А вектор $overrightarrow$,равный вектору $overrightarrow$
Компланарные векторы. Векторный метод решения задач
В параллелепипеде $ABCDA_ B_ C_ D_$, $О$ — точка пересечения диагоналей. Разложите вектор $AО$ по векторам $AB$, $AD$ и $AA_$.
Выберите правильный вариант ответа:
Компланарные векторы. Векторный метод решения задач
DABC – тетраэдр. О – точка пересечения медиан грани BDC. Тогда вектор $overrightarrow$ равен:
Выберите правильный вариант ответа:
Компланарные векторы. Векторный метод решения задач
Восстановите последовательность элементов в доказательстве утверждения поставьте правильную последовательность этапов:
Доказать, что если М – точка пересечения медиан треугольника АВС и О — произвольная точка пространства, то выполняется равенство
Разделим обе части на 3, получим $overrightarrow=frac(overrightarrow+overrightarrow+overrightarrow)$
Так как $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Запишем следующие векторные равенства: $overrightarrow=overrightarrow+overrightarrowoverrightarrow=overrightarrow+overrightarrowoverrightarrow =overrightarrow+overrightarrow$
Сложив эти равенства по частям, получаем: $overrightarrow+overrightarrow+overrightarrow=3overrightarrow+(overrightarrow+overrightarrow+overrightarrow)$
🔍 Видео
№339. Дан параллелепипед ABCDAСкачать

Правило параллелепипеда для векторовСкачать

№357. Даны параллелограммы ABCD и AB1C1D1. Докажите, что векторы ВВ1, СС1 и DD1 компланарны.Скачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

Найдите разложение вектора по векторам (базису)Скачать

№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

10 класс, 44 урок, Правило параллелепипедаСкачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

№116. Дан параллелепипед ABCDA1B1C1D1. Докажите, что: а) DC⊥B1C1, и AB⊥A1DСкачать

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

№82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1ВСкачать

№78. На рисунке 42 изображен параллелепипед ABCDA1B1C1D1, на ребрах которого отмечены точки МСкачать

№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать