Если отрезки не пересекаются то они лежат на параллельных прямых верно или нет (8 видео)

Параллельные прямые. Признаки параллельности прямых

Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Определение 1. Две прямые на плоскости называются параллельными , если они не пересекаются.

Если прямые a и b параллельны, то это обозначают так:

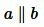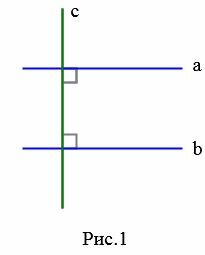
Если отрезки не пересекаются то они лежат на параллельных прямых верно или нет

На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

Понятие параллельности можно распространять и на отрезки.

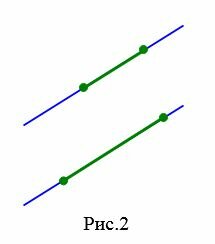
Определение 2. Два отрезка называются параллельными , если они лежат на параллельных прямых (Рис.2).

Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

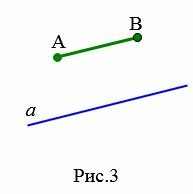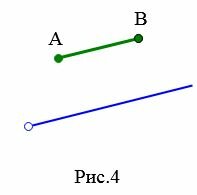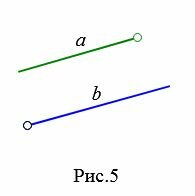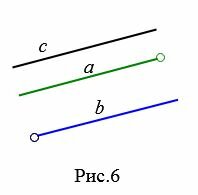На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Содержание

Признаки параллельности прямых
Работа с теоремой «Признак параллельности прямых»
«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
Геометрия. 7 класс
📹 Видео

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

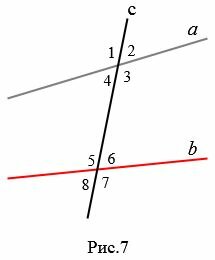накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

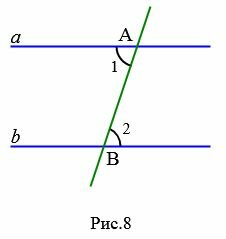Докажем, что .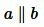

Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

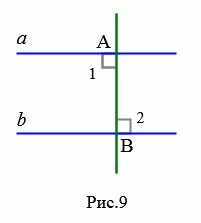Предположим, что углы 1 и 2 не прямые (Рис.10).

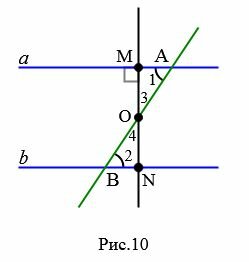Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

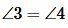
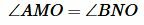
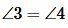
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

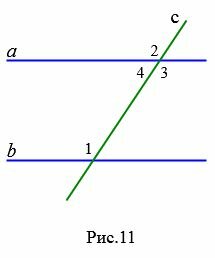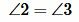
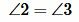
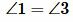
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

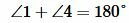
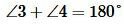
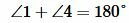
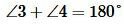
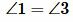
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Работа с теоремой «Признак параллельности прямых»

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Мотивация изучения теоремы и раскрытие ее содержания.

Признак параллельности прямых, который мы сегодня изучим, представлена в первой из 13 книг «Начал» Евклида, то есть известна человечеству уже более 23 веков. Практически этот признак использовали и используют в строительном деле, в частности при строительстве дорог, железнодорожных путей и тому подобное.

Выполнить тестовые задания:

1. На каком рисунке изображены пересекающиеся прямые:

2. Завершить высказывание.

Пересекающиеся прямые имеют…

а) одну общую точку;

б) ни одной общей точки;

в) несколько общих точек.

3. На каком рисунке изображены параллельные прямые

4. Завершить высказывание:

Два отрезка называются параллельными, если они …

оба перпендикулярны третьей прямой.

лежат на параллельных прямых.

имеют одинаковое расстояние между концами

не пересекаются на плоскости.

5. Определите на каком из рисунков угол 1 и угол 2 – смежные.

Ответить на вопросы

1. Какие прямые называются параллельными (ответ учеников – прямые, которые не пересекаются, то есть не имеют ни одной общей точки)?

2. Изобразите и обозначьте параллельные прямые.

3. Какие отрезки называются параллельными? (отрезки, лежащие на параллельных прямых)

4. Изобразите и обозначьте параллельные отрезки

5. Какими будут две прямые перпендикулярные к третьей прямой?

2.Работа над структурой теоремы.

— Оглянемся вокруг. Приведите примеры параллельных прямых, отрезков. (Учащиеся приводят примеры.)

-Ребята, можем ли мы, основываясь на нашем зрении утверждать, что прямые параллельны или не параллельны? (Нет.)

Объясните, почему нельзя этого сделать? (ответ учеников – так как прямые бесконечны, мы не можем их нарисовать, мы рисуем только части прямых).

Какой можно сделать вывод на основании выше сказанного? (ответ учеников –желательно иметь какие-то отличительные свойства или признаки, по которым можно сделать вывод о параллельности двух прямых).

Признак (в геометрии) — это теорема, которая утверждает, что при выполнении определенных условий можно установить взаимное расположение, равенство фигур, принадлежность фигур к определенному классу и тому подобное.

1. Попробуйте перемещением точек А и В добиться параллельности прямой АВ к прямой CD.

2. Сравните образованные при этом соответствующие углы; внутренние накрестлежащие углы.

3. Найдите суммы внутренних односторонних углов.

4. Перемещением точки L установите, сохранятся такие же отношения между углами.

5. Какие условия должны выполняться для параллельности прямых?

3.Построение чертежа и краткая запись содержания теоремы.

Построение чертежа в тетрадях и краткая запись содержания теоремы учащимися.

Теорема (признак параллельности прямых). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если  то АВ‖ CD

4. Поиск доказательства, доказательство и его запись.

оказательство проведем методом от противного. Пусть при пересечении прямых АВ и СВ секущей КL образовались равные соответственные углы  КМВ =  МND.

Предположим, что данные прямые АВ и СD не параллельны, а пересекаются в некоторой точке F. Не меняя меры угла КМВ, перенесем его так, чтобы вершина угла — точка М — совпала с точкой N, луч МК совпал с лучом NМ, а луч MB занял положение луча NF1. Тогда  МNF1 =  КМF . Поскольку луч NF1 не совпадает с лучом NF, так как F  NF1, то  МNF1 ≠  МNF. Но мы установили, что  МNF =  МNF1.

Пришли к противоречию. Поэтому наше предположение о том, что прямые АВ и СD не параллельны, — неправильно. Итак, прямые АВ и СD параллельные, что и требовалось доказать.

Далее рассмотрим следствия с доказанной теоремы.

Следствие 1. Если при пересечении двух прямых секущей внутренние разносторонние углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с внутренние накрест лежащие углы равны, например  1 =  2 .

Поскольку углы 1 и 3 — вертикальные, то они равны:  1 =  3. Итак,  2 =  3. Эти углы — соответственные, поэтому по признаку параллельности прямых имеем:

Следствие 2. Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 °, то прямые параллельны.

Доказательство. Пусть при пересечении прямых а и b секущей сумма внутренних односторонних углов равна 180, например  1 +  2 = 180 °.

Углы 2 и 3 — смежные, поэтому  3 +  2 = 180 °.

Из этих двух равенств следует, что  1 =  3. Эти углы являются соответственными, а поэтому прямые а и b -параллельны по доказанному выше признаку параллельности прямых.

Следствие 3. Две прямые, перпендикулярные к третьей прямой, параллельны.

На рисунке, а _┴ b и b _┴ с. Учитывая следствие 2, имеем: а || b.

Примечание: Следствия 1-3 можно рассматривать как признаки параллельности прямых. Следствие 2 непосредственно следует из пятого постулата Евклида.

Решите задачу по готовому чертежу (устно):

Дано а||в, ∠1=75 о , с – секущая

Найти пары параллельных прямых:

Теорема находит широкое применение при изучении свойств различных фигур и, в частности, четырехугольника.

В параллелограмме ABCD угол A равен 30 о . Чему равен внешний угол при вершине B ?

Заданный параллелограмм ABCD изображен на рисунке. Стороны AD и BC этого параллелограмма лежат на параллельных прямых, а сторона AB на прямой, которая их пересекает. Угол и внешний угол при вершине являются соответственными, а значит, они равны. Следовательно, ∠ОВС=∠А= 30 о .Ответ: 30 о

Решить задачи на готовых чертежах, найти x ,y.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Параллельные прямые.
Накрест лежащие, соответственные, односторонние углы.
Признаки параллельности прямых.
Решение задач на доказательство параллельности прямых.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

накрест лежащие: 3 и 6, 4 и 5.
односторонние: 3 и 5, 4 и 6.
соответственные: 1 и 5, 3 и 7, 2 и 6; 4 и 8.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Дано: ∠1= 60°, ∠2 = 120°.

∠2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;
∠3 = ∠1, это накрест лежащие углы;
Значит, прямые a и b параллельны по 1 признаку параллельности прямых.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Докажите: AB ║ CD.

∠A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.
∠BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.
∠BCD = ∠CDK = 60° т. к. CD – биссектриса делит угол пополам.
Значит, ∠A = ∠DCK = 60° ‑ соответственные, следовательно, AB║CD по 2 признаку параллельности прямых.

Ответ: AB║CD по 2 признаку параллельности прямых.