Существует несколько очень простых, но не эффективных способов преобразования окружностей в растровую форму. Например, рассмотрим для простоты окружность с центром в начале координат. Ее уравнение записывается как x 2 + y 2 = R 2 . Решая это уравнение относительно y , получим
y = ± 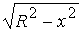
Чтобы изобразить четвертую часть окружности, будем изменять x с единичным шагом от 0 до R и на каждом шаге вычислять y. Вторым простым методом растровой развертки окружности является использование вычислений x и y по формулам x = R cos α, y = R sin α при пошаговом изменении угла α от 0 ° до 90 ° .
Для упрощения алгоритма растровой развёртки стандартной окружности можно воспользоваться её симметрией относительно координатных осей и прямых y = ± x ; в случае, когда центр окружности не совпадает с началом координат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем самым достаточно построить растровое представление для 1/8 части окружности, а все оставшиеся точки получить симметрией (см. рис. 2.5 ).
Рис. 2.5. Восьмисторонняя симметрия
Рассмотрим участок окружности из второго октанта x Є [0, R / 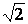
На каждом шаге алгоритм выбирает точку P i ( xi , yi ), которая является ближайшей к истинной окружности. Идея алгоритма заключается в выборе ближайшей точки при помощи управляющих переменных, значения которых можно вычислить в пошаговом режиме с использованием небольшого числа сложений, вычитаний и сдвигов.
Рассмотрим небольшой участок сетки пикселов, а также возможные способы (от A до E ) прохождения истинной окружности через сетку (рис. 2.6 ).
Предположим, что точка Pi —1 была выбрана как ближайшая к окружности при x = xi-1. Теперь найдем, какая из точек ( Si или Ti ) расположена ближе к окружности при x = xi-1 + 1.
Рис. 2.6. Варианты прохождения окружности через растровую сетку
Заметим, что ошибка при выборе точки Pi ( xi , yi ) была равна
Запишем выражение для ошибок, получаемых при выборе точки Si или Ti :
Если | D ( Si ) | ≥ | D ( Ti ) |, то Ti ближе к реальной окружности, иначе выбирается Si .
Ti будет выбираться при di ≥ 0, в противном случае будет устанавливаться Si .
Опуская алгебраические преобразования, запишем di и d i +1 для разных вариантов выбора точки Si или Ti .
Существует модификация алгоритма Брезенхейма для эллипса.
Видео:Графики функций №5.ОкружностьСкачать

Масштабирование изображений
ЛЕКЦИЯ: ГРАФИЧЕСКИЕ ПРОЦЕССОРЫ И РЕДАКТОРЫ
ПОНЯТИЯ КОМПЬЮТЕРНОЙ ГРАФИКИ
Компьютерная графикапредставляет собой одну из современных технологий создания различных изображений с помощью аппаратных и программных средств компьютера, отображения их на экране монитора и затем сохранения в файле или печати на принтере. Существует два способа представления графических изображении: растровый и векторный.
Растровое изображение представляет набор точек, расположенных на сетчатом поле-канве. Каждая точка может принимать различные цвета, по минимуму черный и белый цвет. Область применения- обработка фотографий, рисунков, отсканированных изображений и пр. Достоинством данного вида изображений является возможность передачи большого количества информации (фотографии). Недостатком является большое количество памяти, необходимой для хранения изображения. Для решения этой проблемы применяются способ сжатия изображений с помощью специальных форматов хранения данных (jpg, gif и пр.). К программам работы с растровой графикой относятся: Adobe Photoshop, Corel PhotoPaint, Ms Paint (текстовый редактор).
Векторное изображение представляет набор действий по созданию рисунка с помощью различных линий, фигур, команд заполнения цветом и других команд. Область применения- создание схем, чертежей, рекламных плакатов и пр. Достоинство данного типа — малый объем памяти, занимаемый рисунком. Недостаток — искусственность изображения, состоящее из набора примитивов. Основные программы: Corel Draw, Visio, AutoCad, Arhicad.
Принципы работы в данных программах аналогичны действиям в текстовых и табличных процессорах. При создании нового документа- рисунка необходимо с помощью набора инструментов (кисть, карандаш, ластик, фигуры и линии, распылители и пр.) создать рисунок, как если бы его делали в альбоме. При этом часто можно применять различные команды преобразования, фильтрации и применения различных эффектов с помощью команд в главном меню. Конкретные команды можно изучить используя справочную систему в необходимой для работы программе.
Растровая графика
Наиболее просто реализовать растровое представление изображения. Растр,или растровый массив(bitmap), представляет совокупность битов, расположенных на сетчатом поле-канве. Бит может быть включен (единичное состояние) или выключен (нулевое состояние). Состояния битов можно использовать для представления черного или белого цветов, так что, соединив на канве несколько битов, можно создать изображение из черных и белых точек.

Основным элементом растрового изображения является пиксель (pixel). Под этим термином часто понимают несколько различных понятий: отдельный элемент растрового изображения, отдельная точка на экране монитора, отдельная точка на изображении, напечатанном принтером. Поэтому на практике эти понятия часто обозначают так:
— пиксель— отдельный элемент растрового изображения;
— видеопиксель — элемент изображения на экране монитора;
— точка— отдельная точка, создаваемая принтером или фотонаборным автоматом.
Цвет каждого пикселя растрового изображения — черный, белый, серый или любой из спектра — запоминается с помощью комбинации битов. Чем больше битов используется для этого, тем большее количество оттенков цветов для каждого пикселя можно получить. Число битов, используемых компьютером для хранения информации о каждом пикселе, называется битовой глубиной или глубиной цвета.
Наиболее простой тип растрового изображения состоит из пикселей, имеющих два возможных цвета — черный и белый. Для хранения такого типа пикселей требуется один бит в памяти компьютера, поэтому изображения, состоящие из пикселей такого вида, называются 1-битовыми изображениями. Для отображения большего количества цветов используется больше битов информации. Число возможных и доступных цветов или градаций серого цвета каждого пикселя равно двум в степени, равной количеству битов, отводимых для каждого пикселя. 24 бита обеспечивают более 16 миллионов цветов. О 24-битовых изображениях часто говорят как об изображениях с естественными цветами, так как такого количества цветов более чем достаточно, чтобы отобразить всевозможные цвета, которые способен различать человеческий глаз.
Основной недостатокрастровой графики состоит в том, что каждое изображение для своего хранения требует большое количество памяти. Простые растровые картинки, такие как копии экрана компьютера или черно-белые изображения, занимают до нескольких сотен килобайтов памяти. Детализированные высококачественные рисунки, например, сделанные с помощью сканеров с высокой разрешающей способностью занимают уже десятки мегабайтов. Для разрешения проблемы обработки объемных (в смысле затрат памяти) изображений используются два основных способа:
• увеличение памяти компьютера;
Другим недостатком растрового представления изображений является снижение качества изображений при масштабировании.
Векторная графика
Векторное представление,в отличие от растровой графики, определяет описание изображения в виде линий и фигур, возможно, с закрашенными областями, заполняемыми сплошным или градиентным цветом. Хотя это может показаться более сложным, чем использование растровых массивов, но для многих видов изображений использование математических описаний является более простым способом.
В векторной графике для описания объектов используются комбинации компьютерных команд и математических формул для описания объектов. Это позволяет различным устройствам компьютера, таким как монитор и принтер, при рисовании этих объектов вычислять, где необходимо помещать реальные точки. Векторную графику часто называют объектно-ориентированной или чертежной графикой. Имеется ряд простейших объектов, или примитивов, например: эллипс, прямоугольник, линия. Эти примитивы и их комбинации используются для создания более сложных изображений. Если посмотреть содержание файла векторной графики, обнаруживается сходство с программой. Он может содержать команды, похожие на . слова, и данные в коде ASCII, поэтому векторный файл можно отредактировать с помощью текстового редактора. Приведем в условном упрощенном виде команды, описывающие окружность:
линия: цвет — черный, толщина — 0.50;
Данный пример показывает основное достоинствовекторной графики — описание объекта является простым и занимает мало памяти. Для описания этой же окружности средствами растровой графики потребовалось бы запомнить каждую отдельную точку изображения, что заняло бы гораздо больше памяти. Кроме того, векторная графика в сравнении с растровой имеет следующие преимущества:
• простота масштабирования изображения без ухудшения его качества;
• независимость объема памяти, требуемой для хранения изображения, от выбранной цветовой модели.
Недостаткомвекторных изображений является их некоторая искусственность, заключающаяся в том, что любое изображение необходимо разбить на конечное множество составляющих его примитивов.
Растровая и векторная графика существуют не обособлено друг от друга. Так, векторные рисунки могут включать в себя и растровые изображения. Кроме того, векторные и растровые изображения могут быть преобразованы друг в друга — в этом случае говорят о конвертации графических файлов в другие форматы. Достаточно просто выполняется преобразование векторных изображений в растровые. Не всегда осуществимо преобразование растровой графики в векторную, так как для этого растровая картинка должна содержать линии, которые могут быть идентифицированы программой конвертации (типа CoreiTrace в составе пакета CorelDraw) как векторные примитивы. Это касается, например, высококачественных фотографий, когда каждый пиксель отличается от соседних.
Разрешающая способность
Разрешающая способность — это количество элементов в заданной области. Этот термин применим ко многим понятиям, например, таким как:
• разрешающая способность графического изображения;
• разрешающая способность принтера как устройства вывода;
• разрешающая способность мыши как устройства ввода.
Например, разрешающая способность лазерного принтера может быть задана 300 dpi (dot per inche — точек на дюйм), что означает способность принтера напечатать на отрезке в один дюйм 300 отдельных точек. В этом случае элементами изображения являются лазерные точки, а размер изображения измеряется в дюймах.
Разрешающая способность графического изображения измеряется в пикселях на дюйм. Отметим, что пиксель в компьютерном файле не имеет определенного размера, так как хранит лишь информацию о своем цвете. Физический размер пикселя приобретает при отображении на конкретном устройстве вывода, например, на мониторе или принтере.
Разрешающая способность технических устройств по-разному влияет на вывод векторной и растровой графики.
Так, при выводе векторного рисунка используется максимальное разрешение устройства вывода. При этом команды, описывающие изображение, сообщают устройству вывода положение и размеры какого-либо объекта, а устройство для его прорисовки использует максимально возможное количество точек. Таким образом, векторный объект, например, окружность, распечатанная на принтерах разного качества, имеет на листе бумаги одинаковые положение и размеры. Однако более гладко окружность выглядит при печати на принтере с большей разрешающей способностью, так как состоит из большего количества точек принтера.
Значительно большее влияние разрешающая способность устройства вывода оказывает па вывод растрового рисунка. Если в файле растрового изображения не определено, сколько пикселей на дюйм должно создавать устройство вывода, то по умолчанию для каждого пикселя используется минимальный размер В случае лазерного принтера минимальным элементом служит лазерная точка, в мониторе — видеопиксель. Так как устройства вывода отличаются размерами минимального элемента, который может быть ими создан, то размер растрового изображения при выводе на различных устройствах также будет неодинаков.
Масштабирование изображений
Масштабированиезаключается в изменении вертикального и горизонтального размеров изображения. Масштабирование может быть пропорциональным — в этом случае соотношение между высотой и шириной рисунка не изменяется, а меняется общий размер, и непропорциональным — в этом случае оба измерения изменяются по-разному.
Масштабирование векторных рисунков выполняется просто и без потери качества. Так как объекты векторной графики создаются по их описаниям, то для изменения масштаба векторного объекта, достаточно изменить его описание. Например, чтобы увеличить в два раза векторный объект, следует удвоить значение, описывающее его размер.
Масштабирование растровых рисунков является намного более сложным процессом, чем для векторной графики, и часто сопровождается потерей качества. При изменении размеров растрового изображения выполняется одно из следующих действий:
 |
•одновременное изменение размеров
всех пикселей (в большую или меньшую сторону);
•добавление или убавление пикселей из
рисунка для отражения производимых в
нем изменений, называемое выборкой
пикселей в изображении.
Простейший способ изменения масштаба растрового рисунка состоит в изменении размера всех его пикселей. Так как внутри самого рисунка пиксели не имеют размера и приобретают его уже при выводе на внешнее устройство, то изменение размера пикселей растра в сильной степени похоже на масштабирование векторных объектов — необходимо сменить только описание пикселя, а остальное выполнит устройство вывода.
Устройство вывода для создания пикселя определенного физического размера использует столько своих минимальных элементов (лазерных точек — для лазерного принтера, видеопикселей — для монитора), сколько сможет. При масштабировании изображения количество входящих в него пикселей не меняется, а изменяется количество создаваемых устройством вывода элементов, идущих на построение отдельного пикселя изображения. На рис. 2 показан пример масштабирования растрового изображения — увеличения его в два раза по каждому измерению.
Выборка растрового рисунка может быть сделана двумя различными способами.
По первому способу просто дублируется или удаляется необходимое количество пикселей. При этом в результате масштабирования, как правило, ухудшается качество изображения. Например, при увеличении размера рисунка возрастают его зернистость и дискретность. При уменьшении размера рисунка потери в качестве не столь заметны, однако при последующей восстановлении уменьшенного рисунка до прежнего размера опять возрастают зернистость и дискретность. Это связано с тем, что при уменьшении размера рисунка часть пикселей была удалена из исходного изображения и потеряна безвозвратно, а при последующем восстановлении размеров рисунка недостающие пиксели дублировались из соседних.
По второму способу с помощью определенных вычислений можно создать пиксели другого цвета, определяемого цветами первоначального пикселя и его окружения. Этот метод называется интерполяцией и является более сложным, чем простое дублирование. При интерполяции кроме дублируемых пикселей, отбираются и соседние с ними, с помощью которых вновь создаваемые пиксели получают от существующих усредненный цвет или оттенок серого. В результате переходы между пикселями становятся более плавными, что позволяет убрать или уменьшить эффект «пилообразного» изображения.
Видео:Что такое растровая и векторная графика?Скачать

Алгоритмы Брезенхема растровой дискретизации отрезка
• Установить критерии «хорошей» аппроксимации (отрезок должен начинаться и кончаться в заданных точках и при этом выглядеть сплошным и прямым);
• Кроме того, яркость вдоль отрезка должна быть одинаковой и не зависеть от наклона отрезка и его длины (горизонтальные и вертикальные отрезки всегда будут ярче наклонных, а постоянная яркость вдоль отрезка опять же достигается на вертикальных, горизонтальных и наклоненных под углом в 45° линиях);
• Алгоритм должен работать быстро. Для этого необходимо по возможности исключить операции с вещественными числами;
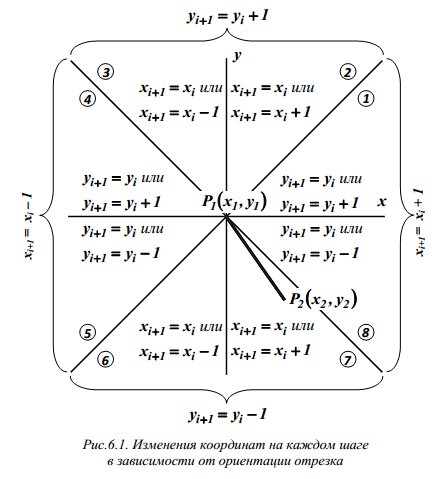
Более приемлемым для генерации отрезков считается алгоритм Брезенхема . В соответствии с ним отрезок вычерчивается пошагово от начала — точки P 1 с координатами ( x 1 , y 1 ) — до конца — точки P 2 с координатами ( x 2 , y 2 ) . Важную роль при этом имеет ориентация отрезка. Ее определяет положение точки P 2 относительно начала координат, которое условно совмещается с точкой P 1 (рис.6.1).
При попадании точки P 2 в какой-либо октант координатной плоскости говорят о том, что весь отрезок расположен в этом октанте (так, например, считается, что отрезок P 1 P 2 на (рис.6.1) расположен в седьмом октанте). На каждом шаге в зависимости от величины тангенса угла наклона отрезка (назовем его угловым коэффициентов и обозначим как m ) единичное приращение одной из координат задается безусловно. Необходимость единичного изменения другой координаты определяется по знаку рассчитываемой на каждом шаге величины e (ошибки), которая оценивает расстояние между действительным положением отрезка и ближайшими по данной координате адресуемыми точками растра. Если модуль углового коэффициента не больше единицы (1, 4, 5 и 8 октанты), на каждом шаге x изменяется на единицу, а y либо не изменяется, либо изменяется на единицу (рис.6.1), в зависимости от знака ошибки. При модуле углового коэффициента больше единицы (2, 3, 6 и 7 октанты), наоборот, y безусловно изменяется на единицу, а знак ошибки используется для принятия решения об изменении величины x . Знак же приращений координат x и y зависит от конкретной ориентации отрезка (так, при генерации отрезка P 1 P 2 , изображенного на рис.6.1, на каждом шаге y безусловно будет получать приращение -1, а x — либо изменяться на +1, либо оставаться неизменным).
Ознакомимся более подробно с принципами работы вещественного алгоритма Брезенхема для генерации отрезка в первом октанте (впоследствии он будет преобразован в целочисленный и обобщен на случай произвольной ориентации отрезка). Значение углового коэффициента отрезка, расположенного в первом октанте, лежит в диапазоне 0 m , и на каждом шаге x безусловно получает приращение +1, а вопрос о приращении y на +1 решается с учетом знака ошибки е. Каким образом она формируется и используется для выбора решения, можно рассмотреть на следующем примере.
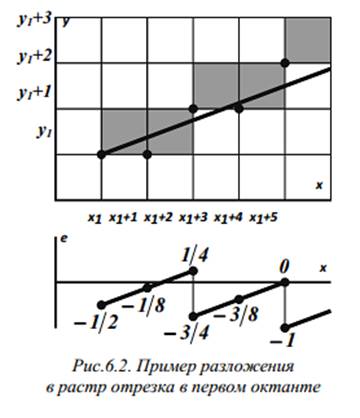
Новое значение ошибки рассчитывается путем добавления к ней значения углового коэффициента: е = е + m = -1/2+3/8 = -1/8 . Отрицательное значение ошибки свидетельствует о том, что пересечение реального отрезка с прямой x = x 1 +1 расположено ближе к прямой y = y 1 , чем к прямой y = y 1 +1 (рис.6.2), поэтому точка растра ( x 1 + 1, y 1 ) лучше аппроксимирует ход отрезка, чем точка ( x 1 + 1, y 1 + 1 ). Активизировав пиксель с координатами адресуемой точки ( x 1 + 1, y 1 ), делаем следующий шаг: x = x 1 + 2, e = e + m =-1/8+3/8=1/4 ; т.к. ошибка положительна, задаем единичное приращение по вертикали y = y 1 +1. Активизируем пиксель с адресуемой точкой ( x 1 + 2 , y 1 +1 ). Вместе с тем, как только ошибка стала положительной, ее значение необходимо скорректировать путем вычитания единицы: e = е -1 = 1/4 -1 = — 3/4 . Дальнейшие действия алгоритма аналогичны: x = x 1 + 3 , e = — 3/4 + 3/8 = — 3/8 , y не увеличивается, активизируется пиксель ( x 1 + 3, y 1 + 1 ) и т.д. Отметим здесь только еще один нюанс: если на каком-либо шаге ошибка принимает нулевое значение, нет предпочтительного варианта задания вертикальной координаты (т.к. отрезок пересекает соответствующую вертикаль строго посередине между двумя узлами растра); для определенности алгоритм Брезенхема в этом случае дает приращение y на единицу и корректирует значение ошибки. Поэтому при расчете следующей точки в рассмотренном только что примере результаты будут такими: x = x 1 + 4, e = -3/8+3/8 = 0 , y = y 1 + 2 , активизация пикселя с координатами адресуемой точки ( x 1 + 4, y 1 + 2 ) , корректировка значения ошибки e = 0 -1 = -1 (см. рис.6.2).
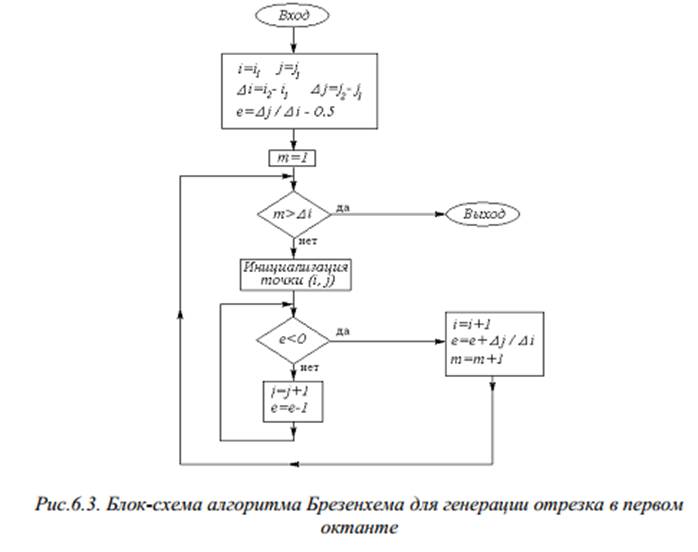
Алгоритм Брезенхема (и его программная реализация) для генерации отрезка в первом октанте на блок-схеме выглядит так:
Uses GraphABC , CRT;
Const i1=100; i2=300; j1=100; j2=300;
Var i ,j,di,dj,m:integer ; e:real;
di :=i2-i1; dj :=j2-j1;
While e>0 do begin
Видео:Лекция 2 | Компьютерная графика | Виталий Галинский | ЛекториумСкачать

 Алгоритм Брезенхема для генерации окружности
Алгоритм Брезенхема для генерации окружности
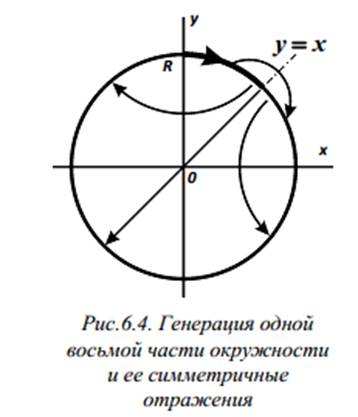
Существуют несколько версий алгоритма Брезенхема для генерации окружности. Они имеют ряд общих признаков. Так, во всех этих версиях изначально пошагово генерируется одна восьмая часть окружности, расположенная во втором октанте координатной плоскости, при условии, что центр окружности совмещен с точкой начала координат (рис. 6.4); причем ее построение начинается в точке ( x = 0, y = R ) и осуществляется в направлении по часовой стрелке.
При этом y является монотонно убывающей функцией x . Остальные части окружности достраиваются последовательными симметричными отражениями: сгенерированной восьмой части во втором октанте — относительно прямой y = x в первый октант, а полученной после этого четверти окружности в первом квадранте — относительно координатных осей x и y , а также точки начала координат в четвертый, второй и третий квадранты соответственно. Во всех случаях арифметика целочислена , при анализе альтернативных вариантов перехода (от пикселя к пикселю) используются не численные значения, а только знаки определенных величин (критериев), что упрощает и ускоряет вычисления. Отличаются версии, по сути дела, только несколько разными с математической, в том числе геометрической точки зрения подходами. Рассмотрим кратко первую, самую раннюю, версию алгоритма (сейчас она практически вышла из употребления) и одну из тех, которые появились позже и применяются в настоящее время.
Теоретические положения, на которых базируется первая версия алгоритма Брезенхема , пригодны для построения четверти (а не одной восьмой части) окружности в первом квадранте. При нахождении в этом квадранте в некоторой текущей точке растра с координатами ( xi , yi ) есть только три варианта выбора очередного пикселя (рис.6.5): по горизонтали вправо (направление H ), по диагонали вниз и вправо (направление D ) и по вертикали вниз (направление V). Вместе с тем, в каждой такай ситуации возможны пять типов пересечений реальной окружности и сетки растра (рис. 6.5).
В качестве первого критерия для выбора очередного шага используется разность между квадратами расстояний от центра окружности до диагональной (по отношению к текущей) точки, т.е. точки с координатами ( xi + 1, yi -1 ), и до реальной окружности: ∆i = ( xi + 1) 2 +( yi -1) 2 — R 2 .
При ∆i диагональная точка находится внутри окружности, т.е. это случаи пересечения 1 или 2. Ясно, что в данной ситуации следует выбрать либо точку ( xi +1 , yi ), т.е. 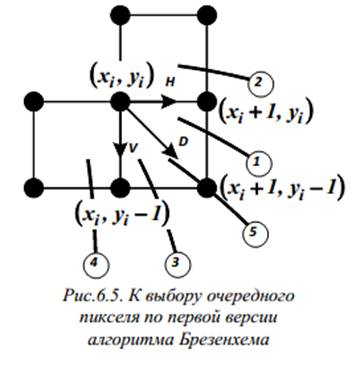
Вторым критерием перехода при таких условиях служит величина: δ= (( xi +1) 2 + yi 2 — R 2 ) – ( ( xi +1) 2 + ( yi -1) 2 — R 2 )
Она представляет собой разность двух модулей: под первым из них стоит разность между квадратами расстояний от центра окружности до горизонтальной (по отношению к текущей) точки и до реальной окружности; под вторым — разность между квадратами расстояний от центра окружности до диагональной (по отношению к текущей) точки и до реальной окружности.
При δ расстояние от окружности до горизонтальной точки не больше расстояния до диагональной точки, и следует выбирать горизонтальную точку, т.е. шаг H .
При δ > 0 выбирается диагональная точка, т.е. шаг D , т.к. расстояние от окружности до нее меньше. Вместе с тем, при варианте пересечения 1 (см. рис.6.5)
( xi +1) 2 + yi 2 — R 2 >= 0 , ( xi +1) 2 + ( yi -1) 2 — R 2 0 , т.к. горизонтальная точка лежит вне или на окружности, а диагональная — внутри нее, поэтому δ можно вычислить по формуле:
При варианте пересечения 2 (см. рис.6.5) расстояние от окружности до горизонтальной точки безусловно меньше расстояния от нее же до диагональной точки, и выбирать следует горизонтальную. При этом обе точки лежат внутри окружности, поэтому: ( xi +1) 2 + yi 2 — R 2 0 , ( xi +1) 2 + ( yi -1) 2 — R 2 0 , и для расчета δ можно использовать ту же формулу, что и при варианте 1, т.к. она дает заведомо отрицательное значение.
Если ∆ i > 0, то диагональная точка находится вне окружности, т.е. это случаи пересечения 3 или 4
(рис.6.5). Выбирать следует либо точку ( xi +1 , yi -1 ), т.е. шаг D , либо точку ( xi , yi -1 ), т.е. шаг V.
Можно показать (аналогично тому, как это было сделано для предыдущего случая), что критерием для выбора при этом является величина δ = 2 ( ∆ i — x i ) -1 .
при δ выбирается диагональная точка, т.к. расстояние от окружности до нее не больше, чем до вертикальной (по отношению к текущей);
при δ >0 выбирается вертикальная точка, т.к. расстояние от окружности до нее меньше, чем до диагональной.
Очевидно, что при ∆ i = 0 диагональная точка ( xi + 1, yi -1 ) расположена непосредственно на окружности (вариант пересечения 5 на рис.6.5), и выбирается именно она.
Подведем итог. Согласно рассматриваемой версии алгоритма Брезенхема :
Если сгенерирована четверть окружности в первом квадранте, для построения полной окружности эту четверть следует симметрично отразить относительно осей x и y и точки начала координат, т.е. активизировать не только выбранные пиксели ( xi , yi ), но и симметричные им пиксели ( xi — yi ) (- xi > yi ) и (- xi > — yi ).
Ниже представлена блок-схема составленная с учетом изложенных соображений алгоритма для прорисовки окружности с исходной генерацией ее четверти:
📽️ Видео
1 2 4 сопряжение окружностейСкачать

Информатика 7 класс (Урок№11 - Растровая графика.)Скачать

Общие сведения о растровой графике (6 класс)Скачать

ОЧЕНЬ ВАЖНЫЙ УРОК. РАЗНИЦА МЕЖДУ ВЕКТОРНОЙ И РАСТРОВОЙ ГРАФИКОЙ. СРАВНИВАЕМ. ДОСТУПНО И БЕЗ ВОДЫСкачать

03 09 Особенности растровой графикиСкачать

РАСТРОВАЯ И ВЕКТОРНАЯ ГРАФИКА. СРАВНЕНИЕ. ДОСТОИНСТВА И НЕДОСТАТКИ. Иллюстратор. Adobe IllustratorСкачать

24 HMI ONI Векторная графика. Сектор окружности.Скачать

Растровая и векторная графикаСкачать

001 | Урок: Векторная и растровая графика. Особенности, свойства, отличия.Скачать

Информатика 10 класс: Растровая и векторная графикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Растровая и векторная графика. Основные понятия. Видеоурок по информатике 5 классСкачать

Информатика 7 класс. Компьютерная графика (УМК БОСОВА Л.Л., БОСОВА А.Ю.)Скачать

Урок 89. Движение по окружности (ч.1)Скачать

ВЕКТОРНАЯ И РАСТРОВАЯ ГРАФИКА в чем разница? Основные отличия, особенности и программы для работы.Скачать

Отличия векторной графики от растровой графикиСкачать

КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

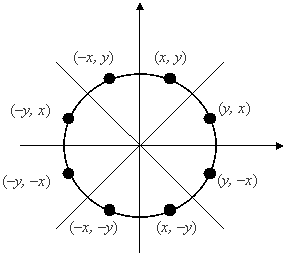

 Алгоритм Брезенхема для генерации окружности
Алгоритм Брезенхема для генерации окружности