В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 6. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MC.
а) Докажите, что сечение плоскостью α пирамиды MABC является параллелограммом.
б) Найдите площадь сечения пирамиды MABC плоскостью α.
а) Пусть точка Q — середина ребра MA, а точка K — середина ребра MB. Плоскость α пересекает плоскость BMC по отрезку KL. Так как плоскость α параллельна ребру MC, то KL || MC, следовательно, KL — средняя линия треугольника AMC, а L — середина ВС. Плоскость α проходит через QK — среднюю линию треугольника MAB, и, следовательно, параллельна AB. Таким образом, пересекает плоскость основания по прямой параллельной AB — средней линии треугольника АВС и проходит через точку O — середину отрезка AC. Значит, сечение — четырёхугольник QKLO, в котором стороны QK и LO параллельны отрезку AB и равны его половине. Значит, QKLO —параллелограмм.
б) Отметим точку F — середину отрезка QK и рассмотрим плоскость MOF. Прямая QK перпендикулярна прямым FM и MO, следовательно, она перпендикулярна плоскости MFO, поэтому она перпендикулярна отрезку OF. Таким образом, отрезок OF служит высотой параллелограмма QKLO. Сечение пирамиды MABCD плоскостью MOF — равнобедренный
треугольник NMG. Отрезок OF является медианой прямоугольного треугольника MOG, проведённой к его гипотенузе, поэтому
По условию треугольник AMC прямоугольный и равнобедренный, поэтому
и то же верно для других боковых рёбер. Следовательно, все боковые грани пирамиды — равносторонние треугольники. Тогда и
Площадь параллелограмма
Ответ:
Примечание от Олега Берковского.
Площадь сечения можно найти проще. Легко доказывается, что сечение KLOQ является ромбом со стороной 3. Меньшая диагональ КО данного ромба также равная 3 (можно получить, рассмотрев треугольник МОВ). Следовательно, ромб состоит из 2-х равносторонних треугольников со стороной 3. Значит, острый угол ромба равен 60 градусов.
Отсюда площадь ромба
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать  Площадь основания пирамидыОснование правильной пирамиды является правильный многоугольник — равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды — это площадь этой плоской фигуры. Видео:В основании пирамиды с вершиной S лежит прямоугольник, центр которого находится на высоте пирамидыСкачать  Площадь основания правильной пирамидыПравильная пирамида может быть трех видов:
Соответственно у правильной треугольной пирамида основание — равносторонний треугольник. У правильной четырехугольной пирамиды основание — квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды: Площадь основания правильной треугольной пирамидыВ основании равносторонний треугольник — находим его площадь:
Основание треугольной пирамиды Площадь основания правильной четырехугольной пирамидыВ основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:
Основание четырехугольной пирамиды Площадь основания правильной шестиугольной пирамидыЭто площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле: Основание шестиугольной пирамиды Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать  Площадь основания любой пирамиды
Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье «Площадь треугольника». В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах. Теперь давайте решим несколько задач для нахождения площади основания пирамиды Видео:10 класс, 33 урок, Правильная пирамидаСкачать  Примеры решения задачЗадача 1Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды. Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: Ответ: Задача 2Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: Теперь подсчитаем, сколько нам понадобится досок: Задача 3Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды. Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:
Видео:ПИРАМИДА Атанасян 242 248 правильная пирамидаСкачать  В основании пирамиды лежит правильный четырехугольникПротивоположные боковые грани правильной четырехугольной пирамиды MABCD с основанием ABCD попарно перпендикулярны. Через середины K и L ребер AB и AD соответственно и точку М проведена плоскость α. а) Докажите, что сечение пирамиды MABCD плоскостью α является равносторонним треугольником. б) Найдите расстояние от точки D до плоскости α, если АВ = 9. Решение: а) Пусть F — середина CD Так как противоположные боковые грани правильной четырехугольной пирамиды MABCD перпендикулярны, то MF⟂ML Пирамида MABCD — правильная, значит проекция вершины M находится в центре основания (квадрата ABCD), то есть в точке О Пусть AB = 2a, тогда AK = AL = a △AKL: KL 2 = AK 2 + AL 2 = a 2 + a 2 = 2a 2 → KL = a√2 △MFL: MO⟂FL, MO — медиана, высота и биссектриса в равнобедренном треугольнике Медиана, проведенная из вершины прямого угла равна половине гипотенузы. Отсюда получаем, что MO = FO = LO = a △MOL: ML 2 = MO 2 + LO 2 = a 2 + a 2 = 2a 2 → ML = a√2 Боковые грани правильной пирамиды — равные равнобедренные треугольники. Так как треугольники равны, то равны и их медианы, то есть MF = ML = MK = a√2 Получаем, что KL = ML = MK = a√2 → △MKL — равносторонний треугольник → сечение пирамиды MABCD плоскостью α является равносторонним треугольником. б) Расстояние от точки D до плоскости α является высотой пирамиды MDKL = ρ. Высоту пирамиды мы будем искать из объема пирамиды MDKL 🎦 ВидеоДемо-вариант ЕГЭ по математике (базовый уровень) #16-3Скачать 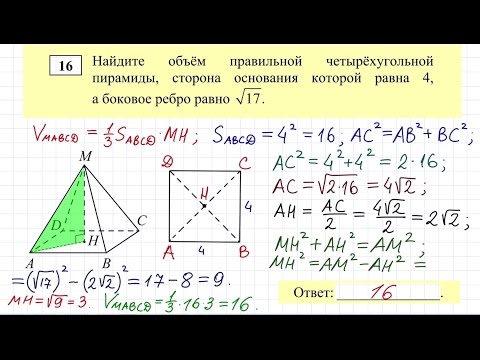 №225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать 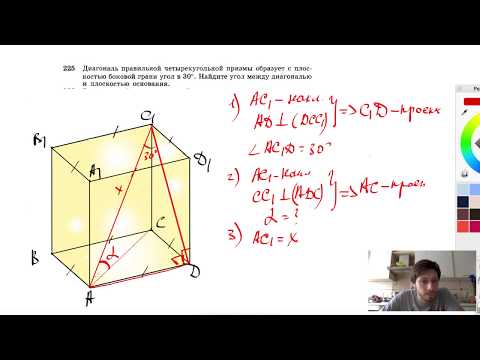 Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать 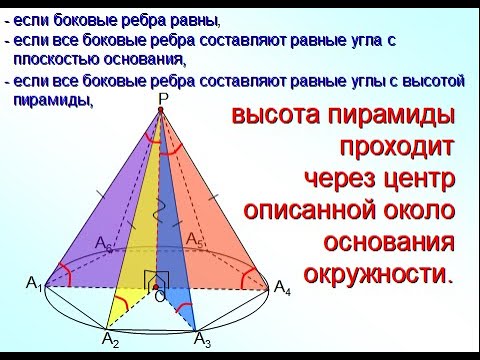 Задача по стереометрии С2. ЕГЭ. Профильный уровень.Скачать  Найти площадь поверхности правильной четырехугольной пирамидыСкачать  ЕГЭ Задание 14 Объем наклонной пирамидыСкачать  СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать  Геометрия 10 класс (Урок№15 - Пирамида.)Скачать  Найдите отрезок АС в правильной четырехугольной пирамидеСкачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  Как рисовать правильный шестиугольник в основанииСкачать  №256. В правильной четырехугольной пирамиде сторона основания равна m, а плоский угол приСкачать  11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать  Найти объем правильной треугольной пирамидыСкачать  11 класс, 35 урок, Объем пирамидыСкачать  |
 , где
, где  — сторона треугольника.
— сторона треугольника.
 , где
, где 


 . Нам дана сторона
. Нам дана сторона  , тогда
, тогда 

 . Подставим в нее значение стороны
. Подставим в нее значение стороны  . Получим:
. Получим:  м 2 .
м 2 . .
.
 .
.
