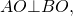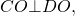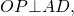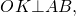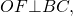Радиус вписанной окружности в трапецию равен половине высоты трапеции.
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность. В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
после небольших преобразований получим
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
И соответственно радиус вписанной окружности в трапецию
- Вписанная в трапецию окружность
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
- 📹 Видео
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
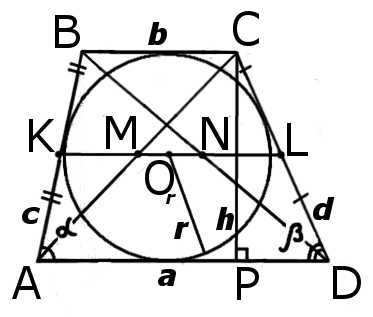
Вписанная в трапецию окружность
Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?
1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.
1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.
O — точка пересечения
биссектрис трапеции ABCD.
3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,
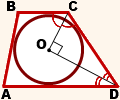
и точка O лежит на средней линии трапеции.
4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:
5.
6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:
Видео:Радиус описанной окружности трапецииСкачать
Трапеция. Формулы, признаки и свойства трапеции
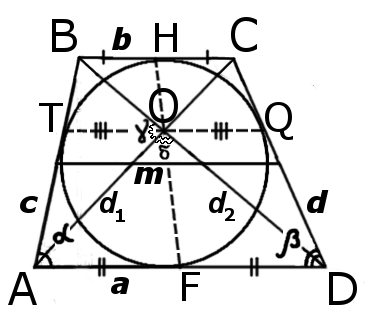
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
 |  |
| Рис.1 | Рис.2 |
Видео:Окружность, вписанная в трапециюСкачать
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Видео:Трапеция и вписанная окружностьСкачать
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Видео:Трапеция вписана в окружность. Найти радиус окружностиСкачать
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Видео:ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
| p = | a + c + d 1 |
| 2 |
a — большее основание
Видео:Радиус и диаметрСкачать
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
📹 Видео
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать
Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Геометрия Докажите, что диаметр окружности вписанной в равнобедренную трапецию есть среднееСкачать
Формулы для радиуса окружности #shortsСкачать
найти радиус окружности, описанной вокруг треугольникаСкачать
Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
