Задание 14. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 8 и ВС = 6. Длины боковых рёбер пирамиды SA= √21, SB = √85, SD = √57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.
а)Рассмотрим треугольник SAB, в котором по условию задания: SA= √21, AB = 8, SB = √57.Можно заметить, что
и согласно обратной теореме Пифагора треугольникSAB – прямоугольный, с гипотенузой SB и катетами SA и AB.
Рассмотрим треугольник SAD со сторонами: SD = √57, SA= √21, AD = 6 (так как в основании пирамиды лежит четырехугольник, поэтому AD = BC). Здесь также:
и по обратной теореме Пифагора имеем прямоугольный треугольник SAD с гипотенузой SD и катетами SA и AD.
Так как 
, то по признаку перпендикулярности прямой и плоскости 
и SA–высота пирамиды.
б)Так как ABCD – прямоугольник, то точка O лежит на пересечении его диагоналей и делит их пополам, то есть, O–середина отрезка BD. Сделаем построение – отрезок KO как средняя линия треугольника SAC, причем, 
. Тогда угол между SC и BDбудет также равен углу KOD.
Найдем косинус угла SOD из треугольника KOD. В соответствии с теоремой косинусов, имеем:
Рассмотрим прямоугольный треугольник SDC (прямоугольный, так как 
и 
— по теореме о трех перпендикулярах получаем, что 
). По теореме Пифагора:
Тогда KO = SC:2 = 11:2. Далее, диагональ
Следовательно, DO = DB:2 = 5. Точка K – середина SA, имеем: 
и
Получаем косинус угла:
Ответ:
Видео:Задание 14 | 2 вариант Ященко ЕГЭ профиль 2021 | В основании четырехугольной пирамиды прямоугольникСкачать
Задание 14. Математика ЕГЭ. В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 8 и BC = 6. Длины боковых ребер пирамиды SA = √21, SB = √85, SD = √57. Докажите, что SA – высота пирамиды. Найдите угол между прямыми SC и BD.
Задание.
В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 8 и BC = 6. Длины боковых ребер пирамиды SA = √21, SB = √85, SD = √57.
а) Докажите, что SA – высота пирамиды.
б) Найдите угол между прямыми SC и BD.
Решение:
а) Докажите, что SA – высота пирамиды.
Рассмотрим треугольник SAB. По теореме, обратной теореме Пифагора (Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный), стороны этого треугольника удовлетворяют равенству:
SB 2 = SA 2 + AB 2
Следовательно, треугольник SAB – прямоугольный,
Рассмотрим треугольник SAD. По теореме, обратной теореме Пифагора, стороны этого треугольника удовлетворяют равенству:
SD 2 = AD 2 + SA 2
Следовательно, треугольник SAD – прямоугольный,
, тогда
Значит, SA – высота пирамиды.
б) Найдите угол между прямыми SC и BD.
SC и BD – скрещивающиеся прямые. Углом между скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым. Пусть точка О – точка пересечения диагоналей BD и AC основания пирамиды. Через точку О проведем прямую KO II SC. Тогда углом между скрещивающимися прямыми SC и BD является угол между прямыми KO и ВD, т.е. ∠KOD.
Так как точка О – середина АС и KO II SC, то точка К – середина SA, т.е. КО – средняя линия треугольника ASC.
SA перпендикулярна плоскости ABC, SB – наклонная к плоскости ABC, АВ – проекция наклонной SB на плоскость ABC. Тока В – основание наклонной, через точку В проходит прямая ВС перпендикулярно проекции АВ (ABCD – прямоугольник), тогда по теореме о трех перпендикулярах прямая ВС перпендикулярна наклонной SB.
Следовательно, треугольник SBC – прямоугольный (∠B = 90˚). По теореме Пифагора найдем SC:
SC 2 = SB 2 + BC 2
SC 2 = (√85) 2 + 6 2 = 121
Так как в основании пирамиды лежит прямоугольник, то треугольник BCD – прямоугольный (∠С = 90˚). По теореме Пифагора найдем BD:
BD 2 = DC 2 + BC 2
BD 2 = 8 2 + 6 2 = 100
Рассмотрим прямоугольный треугольник AKD (∠A = 90˚). По теореме Пифагора найдем DK:
DK 2 = AD 2 + AK 2
По теореме косинусов найдем cos∠KOD:
DK 2 = DO 2 + KO 2 – 2·DO·KO· cos∠KOD
Елена Васильевна! Спасибо за решение ! Очень понравилось! Все четко, ясно и понятно!Успехов Вам!
Видео:МА2010109. В основании пирамиды MABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = 33, все боСкачать
В Основании пирамиды лежит прямоугольник со сторонами 6 и 8 см.
В Основании пирамиды лежит прямоугольник со гранями 6 и 8 см. Верхушка пирамиды равноудалена от вершины основания, а вышина пирамиды одинакова 12. найти. боковую поверхность? Помогите срочнооо необходимо
- Sdobyreva Angelina
- Геометрия 2019-01-13 03:34:21 1 1
Дано:
AB=AC=8 см.
AD=BC=6 см.
SO = 12 см.
Решение:
Sбок = 1/2 * p * l
Обретаем апофему по теореме Пифагора:
P = (a + b) * 2 = (6 + 8) * 2 = 28
d = a^2 + b^2 = 8^2 + 6^2 = 100 = 10
OC = OA^2 + AC^2 = 12^2 + 10^2 = 144 + 100 = 12 + 10 = 22 см.
Sбок = 1/2 * 28 * 22 = 308.
🌟 Видео
В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 6 и диагональю BD = 11.Скачать
СТЕРЕОМЕТРИЯ ЕГЭ | 14 задача 2 вариант Ященко 2021 🔴Скачать
🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать
Ященко. ЕГЭ. Профильная математика. 2 вариант. 2021. 14 задание. GeoGebra.Скачать
Ященко. ЕГЭ. Профильная математика. 22 вариант. 2023. 13 задание. GeoGebra.Скачать
Ященко. ЕГЭ. Профильная математика. 1 вариант. 2023. 13 задание. GeoGebra.Скачать
Угол между прямыми, плоскостями, прямой и плоскостью | Математика ЕГЭ для 10 класса | УмскулСкачать
ЕГЭ Задание 14 Угол между прямыми Координатно векторный методСкачать
Задача по стереометрии С2. ЕГЭ. Профильный уровень.Скачать
Разбор Задачи №14 из Работы СтатГрад от 19 апреля 2019Скачать
Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать
ШУТНИК И ПАЛЬТО (ЗАДАЧА)Скачать
Ященко. ЕГЭ. Профильная математика. 12 вариант. 2022. 13 задание. GeoGebra.Скачать
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основанияСкачать
Все Задания 10 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать
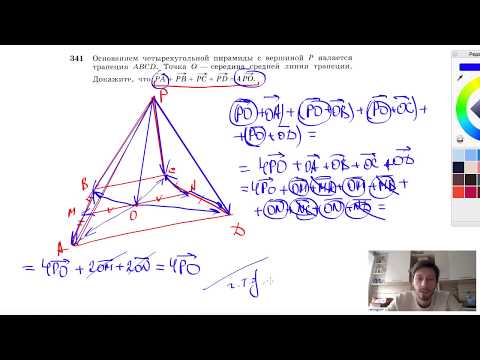
№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать
Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
