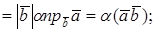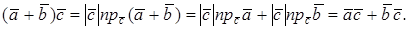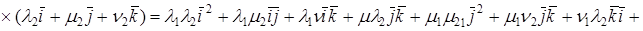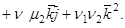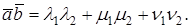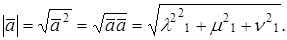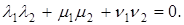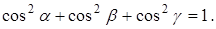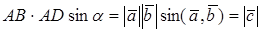Определение 51. Базис Е = (Е1, Е2, . , Еn) пространства Еn называется Ортонормированным, если все его векторы единичные и попарно ортогональные.
Замечание. В примере 1 пункта 7.2 заданный базис является ортонормированным. Во втором примере этого пункта базис не ортонормированный.
Если базисные векторы единичные, но не все попарно ортогональны, то базис называется Нормированным. Если базисные векторы попарно ортогональны, но не все единичные, то базис называется Ортогональным.
Теорема 43. Любой базис евклидова пространства можно ортонормировать.
Доказательство. Пусть Е = (Е1, Е2, . , Еn) – произвольный базис пространства Еn. Доказательство проведём в два этапа. Сначала на основе данного базиса получим ортогональный базис, а затем полученный базис нормируем.
Пусть Е11 = Е1. Если Е2 ^ Е1, То возьмём Е21 = Е2. Если Е2 не ортогонален Е1. то найдём коэффициент A Так, чтобы вектор Е21 = AЕ1 + Е2 Был ортогонален вектору Е11. Так как вектор Е21 ¹ 0, то для этого необходимо и достаточно, чтобы (Е11, е21 ) = 0, т. е. (Е1, AЕ1 + Е2) = 0. Отсюда AЕ12 + (Е1, Е2) = 0. Так как Е1 ¹ 0. то 
Так как определитель этой системы отличен от нуля (по формуле 43) то система имеет и только одно решение. Следовательно,
Вектор Е31 найдётся и только один. Так как векторы Е11, е21, е31 попарно ортогональны, то они линейно независимы. Если векторы Е11, е21, … , еn–11 уже получены, то вектор Еn1 будем искать в виде Еn1 = B1×Е11+ B2× е21 + … + Bn–1× еn–11 + Еn . Так как вектор Еn1 должен быть ортогонален ко всем предыдущим, то для нахождения коэффициентов B1, B2, … , Bn–1 получим систему уравнений (Е11, Еn1) = (Е21, Еn1) = … = (Еn–11, Еn1) = 0. Можно показать, что эта система всегда имеет решение и только одно. Итак, базис Е1 = (Е11, Е21, . , Еn1) –ортогональный. Разделив каждый полученный вектор на его длину, получим ортонормированный базис.
Теорема 44. Скалярное произведение в ортонормированном базисе имеет единичную матрицу Грама.
Доказательство Следует из того, что в ортонормированном базисе (Ек, ек) =1, (Ек, еs )= 0, если К ¹ s.
Следствие. Если вектор А В ортонормированном базисе имеет координаты (Х1, х2,…, хn), то ½А½= 
Теорема 45. Определитель матрицы Грама и все её главные угловые миноры строго положительны.
Доказательство. Пусть в данном (но произвольном) базисе матрица Грама имеет вид
Г = 
Пусть Е = (Е1, Е2, . , Еn) ортонормированный базис и Т – матрица перехода от данного базиса к базису Е. В базисе Е Матрица Грама – единичная. По формуле (43) Е = ТТ×Г×Т. Отсюда 1 = |Г |×|Т |2. Так как |Т |2 > 0,
Так как – евклидово подпространство пространства Еn с Тем же скалярным произведением, то главный угловой минор матрицы Г будет для него матрицей Грама. Но тогда, по доказанному, этот минор положителен.
Примеры. Могут ли быть матрицами Грама следующие матрицы.
1. А =
Матрица А Не может быть матрицей Грама, так как в матрице Грама все диагональные элементы должны быть положительными.
2. В =
Матрица В Не может быть матрицей Грама, так как матрица Грама должна быть симметрична относительно главной диагонали.
3. С =
Матрица С Не может быть матрицей Грама, так как |С | = –81 0, 
Доказательство. В ортонормированном базисе скалярное произведение имеет единичную матрицу, поэтому
(А, В) = ХТ×Е×у = ХТ×у = (Х1, х2, … , хn) × 
Пример. В пространстве Е4 задан ортонормированный базис и векторы А1= (2, 1, 1, 2) и А2 = (–3, 2, –5, 1). Найти ортогональное дополнение к линейной оболочке L = .
Решение. Если L^, то В Î L^ Û (А1, В) = (А2, В) = 0. Пусть В = (Х1, х2, х3, х4). Так как базис ортонормированный, то (А1, В) = 2Х1 + х2 + х3 + 2Х4 , (А2, В) = –3Х1 + 2Х2 –5Х3 + х4 . Следовательно, В Î L^ Û 
В = (–С1 –3С2 , С1 – 8С2 , С1 , 7С2), где С1 , С2 – любые действительные числа.
Отсюда следует, что L^ — двумерное линейное пространство, натянутое на векторы
Видео:Вывод формулы скалярного произведения векторов, заданных координатами в ортонормированном базисе.Скачать

УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
ДОКАЗАТЕЛЬСТВО СВОЙСТВ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Свойство первое следует из определения скалярного произведения: 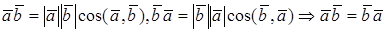
Второе и третье свойства следуют из линейных свойств проекции вектора на ось (направление): 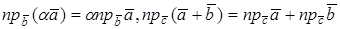
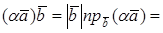
СКАЛЯРНЫЙ КВАДРАТ
Скалярным квадратом называется скалярное произведение 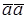
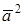
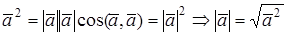
УГОЛ МЕЖДУ ВЕКТОРАМИ
Из определения 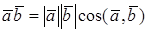
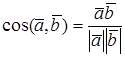
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
Теорема. Векторы 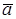
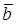
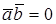
Доказательство необходимости. Пусть 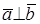
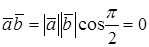

Доказательство достаточности. Пусть 
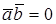
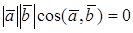
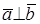
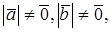
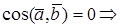
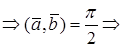
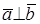
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Теорема. В ортонормированном базисе скалярное произведение векторов 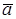
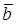
Доказательство. Пусть в пространстве выбран ортонормированный базис 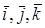
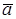
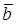
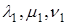

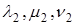
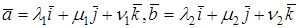
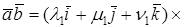
Так как 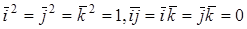
МОДУЛЬ ВЕКТОРА В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Из формулы для скалярного произведения при 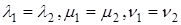
УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
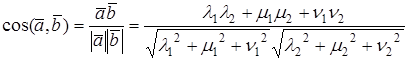
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ В
Если 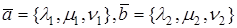
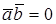
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Определение. Направляющими косинусами вектора 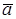
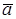
Пусть 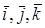
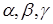
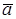
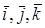
Направляющими косинусами вектора 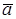

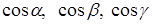
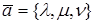
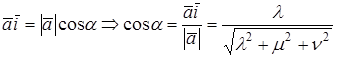
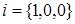
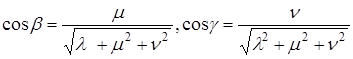
Замечание. Для любого вектора 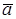
ЛИНЕЙНЫЕ СВОЙСТВА ПРОЕКЦИИ ВЕКТОРА НА ОСЬ
В ортонормированном базисе координаты вектора равны проекциям этого вектора на направления соответствующих базисных векторов.
Действительно, если 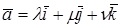
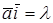
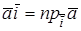
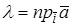
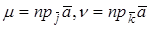
Если 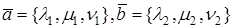
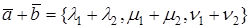
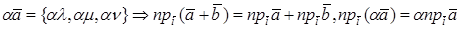
1. Дайте определение скалярного произведения векторов.
2. Выведите условие ортогональности двух векторов.
3. Докажите формулу скалярного произведения векторов в ортогональном базисе.
4. Напишите формулу модуля вектора в ортонормированном базисе.
5. Выведите условие ортогональности двух векторов в ортогональном базисе.
§6. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным произведением вектора 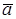
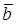
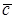
1. 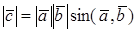
2. 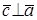
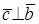
3. Упорядоченная тройка векторов 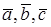
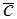
Векторное произведение 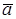
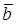
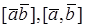
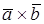
 D C D C   A A  B Рис. 15. B Рис. 15. |  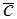   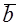 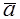  Рис. 14. Рис. 14. |
Замечания. 1. Модуль 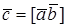
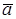
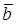
Векторы 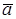
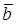
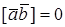
СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. 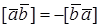
2. 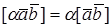
3. 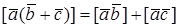
Это свойство примем без доказательства.
ДОКАЗАТЕЛЬСТВО СВОЙСТВ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. Пусть 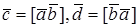
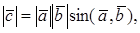
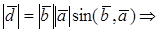
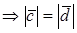
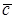
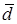
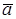
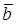
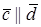
По определению с конца вектора 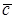
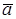
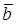
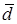
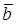
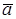
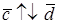
Следовательно, имеем, что 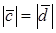
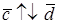
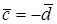
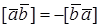
    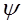 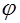 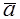 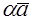 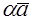  Рис. 16. Рис. 16. |
2. Пусть 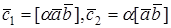
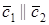
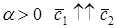
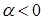
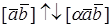
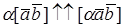
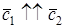
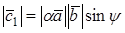
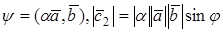
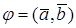
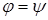
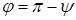
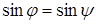
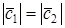
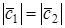
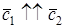
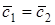
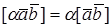
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

В ортонормированном базисе заданы векторы а и б норма
В ортонормированном базисе заданы векторы а=(2; -3;1) b=(-1;2;0). Найти вектор с, перпендикулярный векторам а и b, длина которого равна единице.
Находим вектор d, перпендикулярный двум заданным с помощью векторного произведения.
-1 2 0| -1 2 = 0i – 1j + 4k – 0j – 2i – 3k = -2i – 1j + 1k.
Вектор d = (-2; -1; 1), его модуль равен √((-2)² + (-1)² + 1²) = √6.
Вектор «с» с единичной длиной получим из вектора d, разделив его на его же модуль.
🎦 Видео
Векторное произведение: определение, свойства, вычисление в ортонормированном базисе.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Как разложить вектор по базису - bezbotvyСкачать

Разложение вектора по базису. 9 класс.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Найдите разложение вектора по векторам (базису)Скачать

A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

§48 Ортонормированный базис евклидова пространстваСкачать

Векторное произведение векторовСкачать

Скалярное произведение векторов через координаты. 9 класс.Скачать

Орт вектора. Нормировать вектор. Найти единичный векторСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Лекция 18. Скалярное произведение векторов и его свойства.Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать