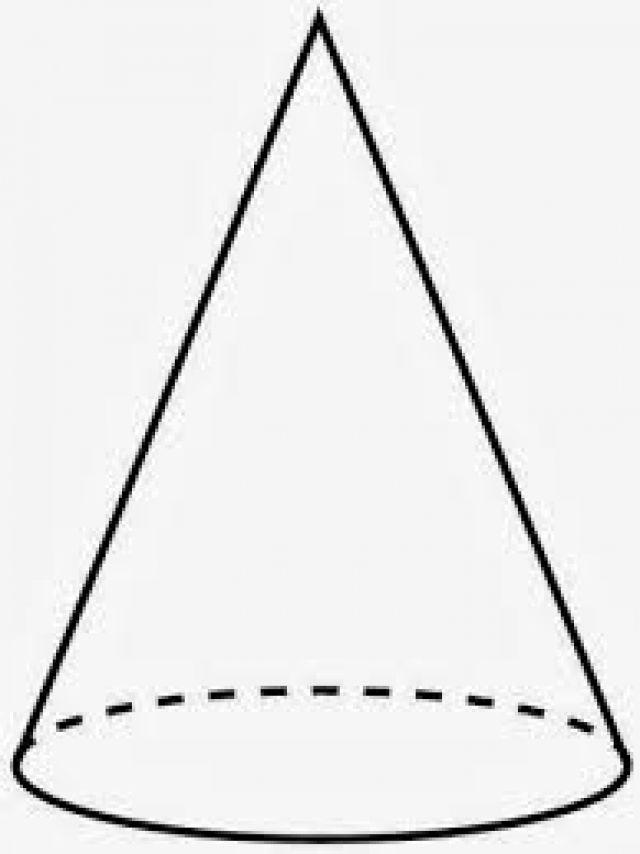
Сечением конуса может быть треугольник окружность прямоугольник круг (7 видео)

Сечением конуса может быть треугольник окружность прямоугольник круг

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a ), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б ), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в ), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г ), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д ). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.

Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = АВ • РC. Имеем: ОР = R (по условию); в △ A OB : ОС = ; в △ ОСР : CP = = .

Тогда S △ ABP = АВ • РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

S бок = α • l 2 , (1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

S кон = π Rl + π R 2 . (3)

Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому

S бок = 2 π ВС • AD. (4)

Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем

= ⇒ BC • AD = DE • АС. (5)

Тогда соотношение (4) принимает вид

S бок = (2 π • DE ) • AC, (6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F 1 , при этом центр О основания отображается на центр О 1 круга F 1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X 1 = РX ∩ α . Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = k, (*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

S сечен : S основ = k 2 = : PO 2 .

18.7. Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

— прямоугольный треугольник (см. рис. 179);

Содержание

Что такое сечение конуса? Как найти площадь осевого сечения конуса
Конус в геометрии
Виды конусов
Геометрические названия элементов конуса
Круглый прямой конус — фигура вращения
Сечения конуса плоскостью, которая не содержит вершину фигуры
Сечения, содержащие вершину конуса
Осевое сечение
Задача на определение линейных параметров конуса
В каких областях важно знать параметры рассмотренных сечений?
Тест по теме «Цилиндр, конус, шар»
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Краткое описание документа:
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
🌟 Видео

Видео:Конус. 11 класс.Скачать

Что такое сечение конуса? Как найти площадь осевого сечения конуса

Одной из фигур, которая встречается при решении геометрических задач в пространстве, является конус. Он, в отличие от многогранников, относится к классу фигур вращения. Рассмотрим в статье, что понимают под ним в геометрии, и исследуем характеристики различных сечений конуса.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Конус в геометрии

Предположим, что имеется некоторая кривая на плоскости. Это может быть парабола, окружность, эллипс и так далее. Возьмем точку, которая указанной плоскости не принадлежит, и соединим с ней все точки кривой. Образованная поверхность называется конической или просто конусом.

Вам будет интересно: Что такое конус: определение. Основание, вершина, высота конуса

Если исходная кривая является замкнутой, тогда коническую поверхность можно заполнить веществом. Полученная таким образом фигура является объемным телом. Она также называется конусом. Несколько конусов, изготовленных из бумаги, показаны ниже на рисунке.

Коническая поверхность встречается в обычной жизни. Например, этой формой обладает мороженое-рожок или дорожный полосатый конус, который призван привлечь внимание водителей и пешеходов.

Видео:№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

Виды конусов

Вам будет интересно: Подберем рифму к слову «капля»

Как можно догадаться, рассматриваемые фигуры друг от друга отличаются типом кривой, на которой они образованы. Например, существует круглый конус или эллиптический. Данная кривая называется основанием фигуры. Однако форма основания — это не единственная особенность, позволяющая классифицировать конусы.

Второй важной их характеристикой является положение высоты относительно основания. Высотой конуса называется прямой отрезок, который опущен из вершины фигуры к плоскости основания и перпендикулярен этой плоскости. Если высота пересекает в геометрическом центре основание (например, в центре круга), то конус будет прямым, если перпендикулярный отрезок падает в любую другую точку основания или за его пределы, то фигура будет наклонной.

Далее в статье будем рассматривать только круглый прямой конус как яркий представитель рассматриваемого класса фигур.

Видео:Геометрия 11 класс (Урок№7 - Конус.)Скачать

Геометрические названия элементов конуса

Выше было сказано, что конус имеет основание. Оно ограничено окружностью, которая называется направляющей конуса. Отрезки, соединяющие направляющую с точкой, не лежащей в плоскости основания, называются образующими. Совокупность всех точек образующих называется конической или боковой поверхностью фигуры. Для круглого прямого конуса все образующие имеют одинаковую длину.

Вам будет интересно: Абашевская культура бронзового века: локализация, археологические находки

Точка, где образующие пересекаются, называется вершиной фигуры. В отличие от многогранников, конус имеет единственную вершину и не имеет ни одной грани.

Прямая линия, проходящая через вершину фигуры и центр круга, называется осью. Ось содержит в себе высоту прямого конуса, поэтому она с плоскостью основания образует прямой угол. Эта информация важна при вычислении площади осевого сечения конуса.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Круглый прямой конус — фигура вращения

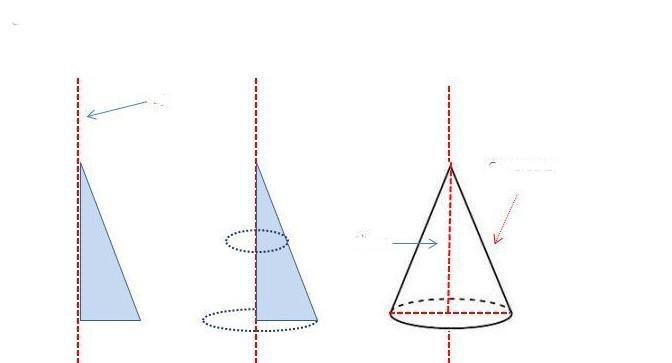
Рассматриваемый конус является достаточно симметричной фигурой, которую можно получить в результате вращения треугольника. Предположим, что имеется треугольник с прямым углом. Чтобы получить конус, достаточно вращать этот треугольник вокруг одного из катетов так, как показано на рисунке ниже.

Видно, что ось вращения является осью конуса. Один из катетов будет равен высоте фигуры, а второй катет станет радиусом основания. Гипотенуза треугольника в результате вращения опишет коническую поверхность. Она будет образующей конуса.

Указанный способ получения круглого прямого конуса удобно использовать для изучения математической связи между линейными параметрами фигуры: высоты h, радиуса круглого основания r и направляющей g. Соответствующая формула следует из свойств прямоугольного треугольника. Она приведена ниже:

Поскольку мы имеем одно уравнение и три переменных, то это означает, что для однозначного задания параметров круглого конуса необходимо знать две любые величины.

Видео:Цилиндр, конус, шар, 6 классСкачать

Сечения конуса плоскостью, которая не содержит вершину фигуры

Вопрос построения сечений фигуры не является тривиальным. Дело в том, что форма сечения конуса поверхностью зависит от взаимного расположения фигуры и секущей.

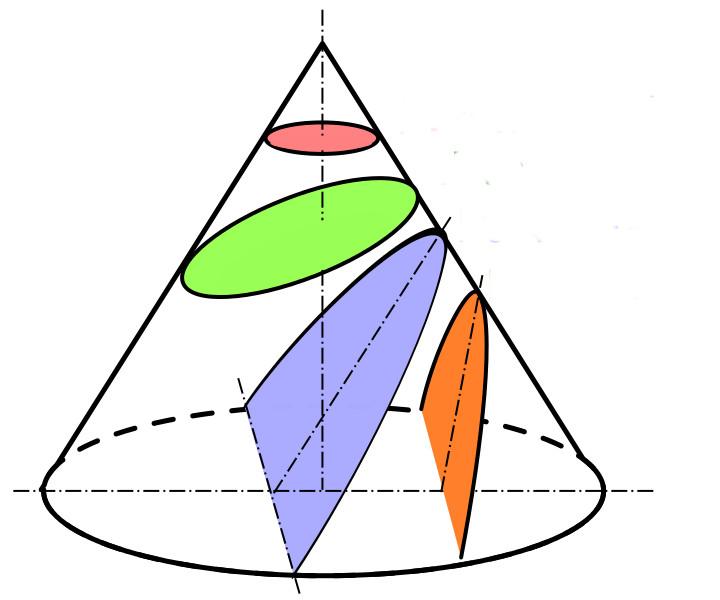
Предположим, что мы пересекаем конус плоскостью. Какое сечение получится в результате этой геометрической операции? Варианты формы сечения показаны на рисунке ниже.

Розовое сечение является кругом. Оно образовано в результате пересечения фигуры плоскостью, которая параллельна основанию конуса. Это сечения перпендикулярно оси фигуры. Образованная выше секущей плоскости фигура представляет собой конус, подобный исходному, но имеющий круг меньшего размера в основании.

Зеленое сечение — это эллипс. Он получается, если секущая плоскость не параллельна основанию, однако она пересекает только боковую поверхность конуса. Отсеченная выше плоскости фигура называется эллиптическим наклонным конусом.

Синее и оранжевое сечения имеют форму параболы и гиперболы, соответственно. Как видно из рисунка, они получаются, если секущая плоскость одновременно пересекает боковую поверхность и основание фигуры.

Для определения площадей сечений конуса, которые были рассмотрены, необходимо использовать формулы для соответствующей фигуры на плоскости. Например, для круга это умноженное на квадрат радиуса число Пи, а для эллипса — это произведение Пи на длину малой и большой полуосей:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сечения, содержащие вершину конуса

Теперь рассмотрим варианты сечений, которые возникают, если секущая плоскость будет проходить через вершину конуса. Возможны три случая:

Сечение — единственная точка. Например, проходящая через вершину и параллельная основанию плоскость дает именно такое сечение.

Сечение — прямая. Эта ситуация возникает, когда плоскость является касательной к конической поверхности. Прямая сечения в этом случае будет образующей конуса.

Осевое сечение. Оно образуется, когда плоскость содержит не только вершину фигуры, но и всю ее ось. При этом плоскость будет перпендикулярна круглому основанию и разделит конус на две равные части.

Очевидно, что площади первых двух видов сечений равны нулю. Что касается площади сечения конуса для 3-го вида, то этот вопрос подробнее рассматривается в следующем пункте.

Видео:№551. Осевое сечение конуса — правильный треугольник со стороной 2г. Найдите площадь сечения,Скачать

Осевое сечение

Выше отмечалось, что осевым сечением конуса называется фигура, образованная при пересечении конуса плоскостью, проходящей через его ось. Несложно догадаться, что это сечение будет представлять фигуру, показанную на рисунке ниже.

Это равнобедренный треугольник. Вершина осевого сечения конуса — это вершина этого треугольника, образованная пересечением одинаковых сторон. Последние равны длине образующей конуса. Основание треугольника — это диаметр основания конуса.

Вычисление площади осевого сечения конуса сводится к нахождению площади полученного треугольника. Если изначально известны радиус основания r и высота h конуса, тогда площадь S рассматриваемого сечения будет равна:

Это выражение является следствием применения стандартной формулы для площади треугольника (половина произведения высоты на основание).

Отметим, что если образующая конуса будет равна диаметру его круглого основания, то осевое сечение конуса — треугольник равносторонний.

Треугольное сечение образуется тогда, когда секущая плоскость перпендикулярна основанию конуса и проходит через его ось. Любая другая плоскость, параллельная названной, даст в сечении гиперболу. Однако если плоскость содержит вершину конуса и пересекает его основание не через диаметр, то полученное сечение тоже будет равнобедренным треугольником.

Видео:Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать

Задача на определение линейных параметров конуса

Покажем, как пользоваться записанной для площади осевого сечения формулой для решения геометрической задачи.

Известно, что площадь осевого сечения конуса равна 100 см2. Полученный в сечение треугольник является равносторонним. Чему равны высота конуса и радиус его основания?

Поскольку треугольник равносторонний, то его высота h связана с длиной стороны a следующим соотношением:

Учитывая, что сторона треугольника в два раза больше радиуса основания конуса, и подставляя это выражение в формулу для площади сечения, получаем:

Тогда высота конуса равна:

Остается подставить значение площади из условия задачи и получить ответ:

r = √(100/√3) ≈ 7,60 см;

h = √(√3*100) ≈ 13,16 см.

Видео:Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

В каких областях важно знать параметры рассмотренных сечений?

Изучение различных типов сечений конуса представляет не только теоретический интерес, но также имеет практическое приложение.

Во-первых, следует отметить область аэродинамики, где с помощью конических сечений удается создавать идеальные гладкие формы твердых тел.

Во-вторых, конические сечения являются траекториями, по которым движутся космические объекты в гравитационных полях. Какой конкретно вид сечения представляет траектория движения космических тел системы, определяется соотношением их масс, абсолютных скоростей и расстояний между ними.

Видео:сечения конусаСкачать

Тест по теме «Цилиндр, конус, шар»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Решение задач на конусСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Тест по теме «Цилиндр, конус, шар»

I . Цилиндр нельзя получить вращением …

1) треугольника вокруг одной из сторон;

2) квадрата вокруг одной из сторон;

3) прямоугольника вокруг одной из сторон.

II . Площадь боковой поверхности цилиндра можно вычислить по формуле …

III . Сечением цилиндра плоскостью, перпендикулярной его образующей, является …

1) круг; 2) прямоугольник; 3)трапеция

IV . На основаниях цилиндра взяты две непараллельные друг другу хорды, не проходящие через центры оснований. Тогда расстояние между хордами …

1) равно высоте цилиндра;

2) больше высоты цилиндра;

3) меньше высоты цилиндра.

V . Наибольший периметр имеет сечение конуса плоскостью, проходящей через его вершину и хорду, стягивающую дугу в …

1) 60º; 2) 90º; 3) 180º.

VI. a- образующая конуса, b — высота конуса. Тогда верно, что …

VII. Через вершину конуса — точку А и хорду ВС проведена плоскость. Тогда угол между этой плоскостью и плоскостью основания это угол …

1) АВО, где АО — высота конуса;

2) АМО, где М — середина хорды ВС;

VIII . Разверткой боковой поверхности конуса является круговой …

1) сегмент; 2) сектор; 3) слой.

IX. Плоскость имеет со сферой только одну общую точку, если расстояние от центра сферы до плоскости …

1) больше ее радиуса; 2) меньше ее радиуса; 3) равно ее радиусу.

Х. Можно провести бесконечное множество касательных плоскостей к данной сфере через … 1) прямую, проходящую вне сферы; 2) точку, лежащую вне сферы;

3) точку, лежащую на сфере;

XI. Радиус шара равен 17 см. Тогда площадь сечения шара плоскостью, находящейся на расстоянии 15 см от центра, равна .

XII. Все стороны правильного треугольника касаются сферы диаметром 12 см, плоскость треугольника удалена на расстояние 3 см от центра сферы. Тогда сторона треугольника равна .

Тест по теме «Цилиндр, конус, шар»

I. Площадь сферы радиуса R можно вычислить по формуле …

II. Сечение сферы есть окружность, если расстояние от центра сферы до плоскости …

1) больше ее радиуса; 2) меньше ее радиуса; 3) равно ее радиусу.

III. Можно провести бесконечное множество сфер через …

1) одну и ту же окружность; 2) окружность и точку, не принадлежащую ей;

3) четыре точки, являющиеся вершинами ромба.

IV . Все вершины параллелограмма ABCD принадлежат сфере. Тогда ABCD не может быть …

1) ромбом; 2) квадратом; 3) прямоугольником.

V . Боковой поверхностью цилиндра высотой Н и диаметром основания d является квадрат. Тогда верно, что …

VI . Разверткой боковой поверхности цилиндра не может быть …

1) прямоугольник; 2) ромб; 3) квадрат.

VII. Площадь боковой поверхности цилиндра больше площади осевого сечения цилиндра в …

1) 1/ π раз; 2) 2 раза; 3) π раз.

VIII . Площадь полной поверхности конуса равна …

IX. Конус может быть получен вращением …

1) равностороннего треугольника вокруг его стороны;

2) прямоугольного треугольника вокруг одного из его катетов;

3) прямоугольного треугольника вокруг гипотенузы.

X. Сечением конуса плоскостью, перпендикулярной оси цилиндра, является …

1) треугольник; 2) прямоугольник; 3) круг.

XI. Радиус основания конуса равен 5 см, а высота 12 см. Тогда длина образующей равна.

XII. Высота цилиндра 6 см, радиус основания 5 см. На расстоянии 4 см от оси цилиндра, параллельно ей, проведено сечение. Тогда площадь сечения равна …

Тест по теме «Цилиндр, конус, шар»

I. Конус может быть получен вращением …

1) прямоугольного треугольника вокруг гипотенузы;

2) равнобедренного треугольника вокруг медианы, проведенной к основанию;

3) тупоугольного треугольника вокруг одной из его сторон.

II. Площадь боковой поверхности конуса можно вычислить ро формуле …

III. Сечением конуса плоскостью, проходящей через вершину конуса и хорду основания, не может быть …

1) равносторонний треугольник; 2) равнобедренный треугольник; 3) разносторонний треугольник.

IV. Через вершину конуса — точку С и хорду АВ проведена плоскость. Тогда угол между этой плоскостью и плоскостью основания — это угол .

1) АСВ; 2) ОАС, где О — центр основания; 3) СКО, где К — середина хорды АВ.

V. Можно провести только одну касательную плоскость к данной сфере через …

1) прямую, проходящую вне сферы; 2) точку, лежащую вне сферы;

3) точку, лежащую на сфере.

V I. Все стороны ромба АВС D касаются сферы с центром в точке О. M, N, P, K — точки касания. Тогда верно, что …

1) ОА=ОВ=ОС=О D; 2) равны углы ОАС, ОВ D, ОСА, О D В; 3) ОМ=О N =ОР=ОК.

VII. Сфера и плоскость не имеют общих точек, если расстояние от центра сферы до плоскости …

1) больше ее радиуса; 2) меньше ее радиуса; 3) равно ее радиусу.

VIII . Все вершины четырехугольника ABCD принадлежат сфере. Тогда ABCD не может быть …

1) прямоугольником; 2) равнобедренной трапецией; 3) прямоугольной трапецией.

IX. Боковой поверхностью цилиндра с высотой Н и радиусом основания R является квадрат. Тогда верно, что, …

1) Н/ R = 2 π; 2) R/ Н = 2 π; 3) Н = 2 R.

Х. Площадь боковой поверхности цилиндра в 3 раза больше площади основания. Тогда отношение Н/ R равно …

Х I. Радиус основания цилиндра 2 см, высота 3 см. Тогда длина диагонали осевого сечения равна …

XII. Высота цилиндра 8 см, радиус основания 5 см. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Тогда расстояние от этого сечения до оси цилиндра равно …

Тест по теме «Цилиндр, конус, шар»

I . Цилиндр можно получить вращением…

1) трапеции вокруг одного из оснований;

2) ромба вокруг одной из диагоналей;

3) прямоугольника вокруг одной из сторон.

II . Площадь полной поверхности цилиндра можно вычислить по формуле …

1) S= πR²+2πRH; 2) S= πR²+πRH; 3)S= 2πR²+2πRH .

III . На основаниях цилиндра взяты две непараллельные друг другу хорды, не проходящие через центры оснований. Тогда расстояние между хордами …

1) равно образующей цилиндра; 2) больше высоты цилиндра;

3) меньше образующей цилиндра.

IV . ABCD – осевое сечение цилиндра. В и С – точки верхнего основания, А и D – нижнего. Точка К делит дугу AD в отношении АК : К D = 1 : 2. Тогда угол АКС равен …

1) 90º; 2) 60º; 3) 30º.

V . Геометрическим местом точек*, равноудаленных от всех образующих конуса, является …

1) центр основания конуса; 2) ось конуса; 3) диаметр основания конуса.

VI . Наибольшую площадь имеет сечение конуса плоскостью, проходящей через его вершину и хорду, стягивающую дугу в …

1) 60º; 2) 90º; 3) 180º.

VII . Две образующие конуса взаимно перпендикулярны. Может ли угол в развертке конуса быть равным 252º ?

1) Может; 2) не может; 3) две образующие конуса не могут быть взаимно перпендикулярны.

VIII . Осевое сечение конуса – прямоугольный треугольник с гипотенузой 12 см. Тогда высота конуса равна … 1) 6 см; 2) 6√2 см; 3) 8 см.

IX . Площадь сферы диаметра d можно вычислить по формуле …

Х. Расстояние между центрами двух сфер радиусов 4 и 7 равно 2. Тогда множество общих точек этих сфер …

1) окружность; 2) единственная точка; 3) пустое множество.

XI . Расстояние от концов диаметра шара до касающейся его плоскости равно 3 см и 7 см. Тогда радиус шара равен …

XII . Все стороны квадрата касаются сферы диаметром 50 см, сторона квадрата равна 14см. Тогда расстояние от центра сферы до плоскости квадрата равно …

*Геометрическим местом точек (ГМТ) называется множество точек, обладающих определенным характеристическим свойством. Например: Серединный перпендикуляр к отрезку есть ГМТ, равноудалённых от концов отрезка.

Окружность — ГМТ, равноудалённых от данной точки, называемой центром окружности.

Краткое описание документа:

Предложены четыре варианта тестов по теме «Цилиндр, конус, шар». Каждый тест состоит из 12 вопросов и задач двух уровней. Первые десять — задания с выборочной формой ответа — проверяют знания определений, формул, формулировок теорем. Задания данного уровня требуют от учащихся умения подводить объект под понятие, выводить следствия из факта, составлять обратные, противоположные и обратные противоположным предложения, опровергать утверждения. Последние два вопроса требуют краткого ответа и направлены на проверку умения применять теоретические знания, решать задачи по стереометрии. Тесты рассчитаны на 20-25 минут. Их можно использовать как для организации контроля на уроке, так и для подготовки к обобщающему уроку или зачету по теме, в качестве домашнего задания. Ко всем тестам приведены ответы.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 964 человека из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 677 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 311 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Тема 6. Конус. Осевое сечение конуса. Развертка боковой поверхности конуса. Площадь боковой и полнойСкачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 523 283 материала в базе

Материал подходит для УМК

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

Глава 6. Цилиндр, конус, шар

Другие материалы

06.11.2021
183
5

06.11.2021
46
0

06.11.2021
106
0

06.11.2021
293
5

06.11.2021
48
1

06.11.2021
70
0

06.11.2021
86
2

05.11.2021
335
50

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

06.11.2021 2405
DOCX 59.5 кбайт
146 скачиваний
Оцените материал:

Настоящий материал опубликован пользователем Чесакова Маргарита Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 5 лет и 3 месяца
Подписчики: 4
Всего просмотров: 28511
Всего материалов: 31

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Ингушетии школьников переведут на дистанционное обучение с 3 по 5 февраля

Время чтения: 1 минута

Ставропольских школьников с 1 по 8 класс перевели на дистанционное обучение

Время чтения: 2 минуты

Новые курсы: педагогический дизайн, ФГОС 2021, управление школой и другие

Время чтения: 14 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.