Эпюра Монжа или комплексный чертеж — это чертеж, составленный из двух или более связанных между собой ортогональных проекций геометрической фигуры.
Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры. Поэтому вместо изображения на чертеже пространственного макета используется эпюра Монжа.
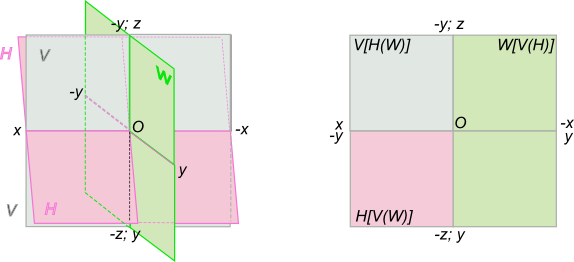
Эпюра Монжа получается преобразованием пространственного макета путем совмещения плоскостей H и W с фронтальной плоскостью проекций V: — для совмещения плоскости H с V поворачиваем ее на 90 градусов вокруг оси x в направлении движения часовой стрелки. На рисунке, для наглядности, плоскость H повернута на угол чуть меньший 90 градусов, при этом ось y, принадлежащая горизонтальной плоскости проекции, после поворота совпадает с осью z; — после совмещения горизонтальной плоскости, поворачиваем вокруг оси z также на угол 90 градусов профильную плоскость в направлении противоположном движению часовой стрелки. При этом ось y, принадлежащая профильной плоскости проекции, после поворота совпадает с осью x.
После преобразования пространственный макет примет вид, показанный на рисунке. На этом рисунке указана также последовательность взаимного положения пол плоскостей проекций, так запись V[H(W)] указывает, что в этой части эпюра Монжа (ограниченного положительным направлением осей x и z) ближе к нам находится верхняя левая пола фронтальной плоскости проекции V, за ней располагается задняя левая пола горизонтальной плоскости проекции H, далее следует верхняя задняя пола профильной плоскости W.
Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Излишне также напоминать, где отрицательное направление координатных осей. Тогда, в окончательном виде эпюра Монжа, заменяющая чертеж пространственного макета примет вид, показанный на рисунке.
Эпюра Монжа может быть выполнена с помощью: — обычных чертежных инструментов и приспособлений: Чертежные инструменты; Чертежные принадлежности и приборы; — Программы для построения (рисования) эпюра Монжа: Выполнение чертежа в графическом редакторе.
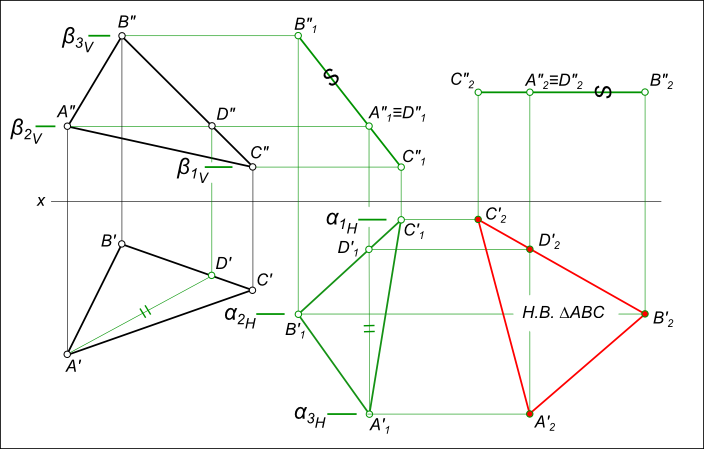
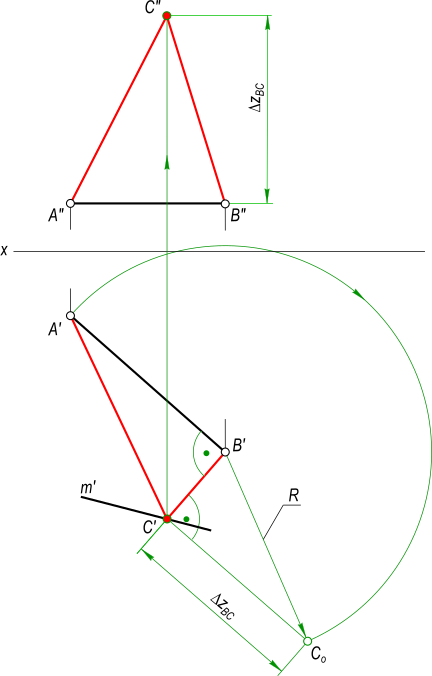
В качестве примера оформления эпюра Монжа предлагаем решение задачи на построение равнобедренного прямоугольного треугольника ABC:
— в черном цвете отображается известное по условию задачи; — в зеленом цвете отображаются все построения которые ведут к решению задачи; — в красном цвете отображается найденные искомые задачи. По условию задачи заданы проекции треугольника ABC(A`B`C`, A»B». «). Для решения задачи необходимо найти недостающую проекцию C».
- Методы преобразования эпюра Монжа в начертательной геометрии с примерами
- Метод замены (перемены) плоскостей проекций
- Метод вращения вокруг проецирующих осей
- Вращение вокруг линий уровня (горизонтали или фронтали)
- Метод совмещения
- Метод плоско-параллельного перемещения
- Построить натуральную величину треугольника авс
- Метки
- Натуральная величина треугольника с описанием.
- Алгоритм определения натуральной величины плоскости:
- Замена плоскостей проекции
- Плоскопараллельное перемещение
- 🎦 Видео
Видео:ЗАДАЧИ ПО ОСНОВАМ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ. МЕТОДЫ ПРОЕЦИРОВАНИЯ И ЭПЮРЫ ТОЧЕК. №1Скачать

Методы преобразования эпюра Монжа в начертательной геометрии с примерами
Содержание:
Методы преобразования эпюра Монжа:
Как видно из предыдущего материала, все геометрические задачи решаются проще, если объекты (или хотя бы один объект) заданы в частном положении.
Для перевода объектов из общего положения в частное с целью упрощения решения задач разработаны методы преобразования эпюра Монжа. Они делятся на два вида:
- Геометрический объект при преобразовании остается неподвижным, а плоскости проекций меняют свое положение так, чтобы объект находился относительно них в частном положении (метод перемены или замены плоскостей проекций);
- Плоскости проекций при преобразовании остаются неподвижными , а объект меняет свое положение так, чтобы относительно плоскостей проекций он занял частное положение (метод вращения вокруг проецирующей оси, метод совмещения, метод вращения вокруг линий уровня, метод плоско-параллельного перемещения).
Видео:Задание: ЭпюрСкачать

Метод замены (перемены) плоскостей проекций
Смысл метода заключается в том, что в систему плоскостей проекций вводятся дополнительные плоскости проекций, по отношению к которым объект занимает частное положение (другими словами, плоскости проекций заменяются другими плоскостями). Ортогональность новых систем плоскостей проекций при этом сохраняется.
Замена плоскостей проекций осуществляется в последовательности:
Обычно производят одну или две замены плоскостей проекций.
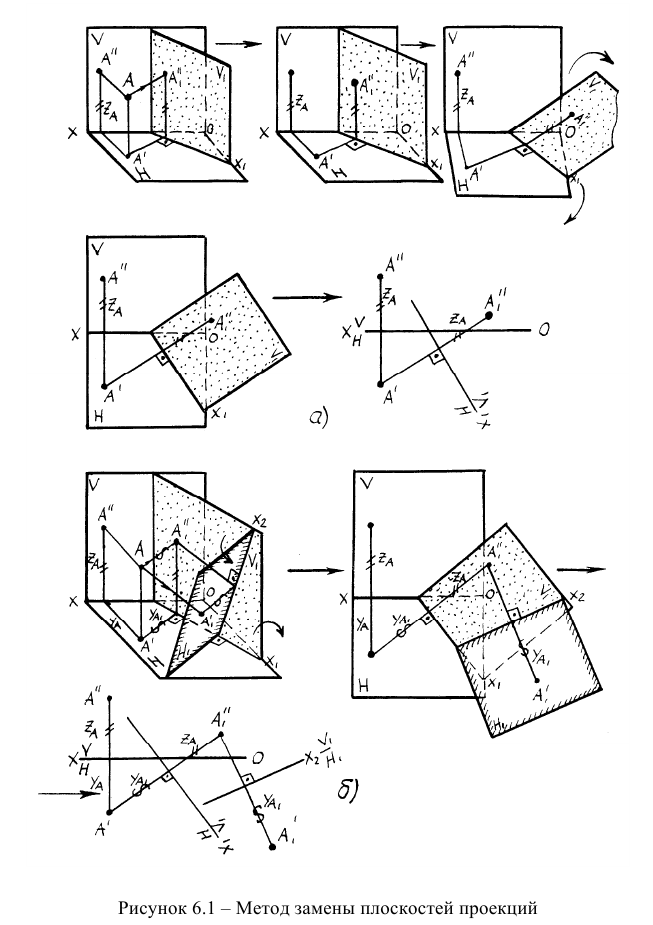
На рисунке 6.1 в наглядной форме показана методика проведения замены плоскостей проекций. На рисунке 6.1а представлена замена одной фронтальной плоскости проекций (V —> Vi), а на рисунке 6.16 — замена двух плоскостей проекций
Из представленных наглядных изображений и эпюров вытекают следующие правила построения новых фронтальных и горизонтальных проекций точки на дополнительные плоскости проекций:
- 1) ПРИ ЗАМЕНЕ ПЛОСКОСТИ V на
. Для того, чтобы построить новую фронтальную проекцию точки на новой плоскости проекций
необходимо от новой оси по новой линии связи отложить аппликату точки из предыдущей системы плоскостей проекций.
- 2) ПРИ ЗАМЕНЕ ПЛОСКОСТИ Н на
Для того, чтобы построить новую горизонтальную проекцию точки на новой плоскости проекций
необходимо от новой оси по новой линии связи отложить ординату точки из предыдущей системы плоскостей проекций.
В методе замены плоскостей проекций выделяют две основные задачи:
- Перевод прямой общего положения в проецирующую;
- Перевод плоскости общего положения в проецирующую.
На рисунке 6.2а показано преобразование прямой общего положения в проецирующую прямую, которое выполнено двумя заменами плоскостей проекций 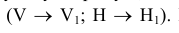
прямой AВ, а вторая — перпендикулярно прямой АВ. Следует заметить, что при решении задачи определяется натуральная величина прямой (новая фронтальная проекция 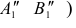
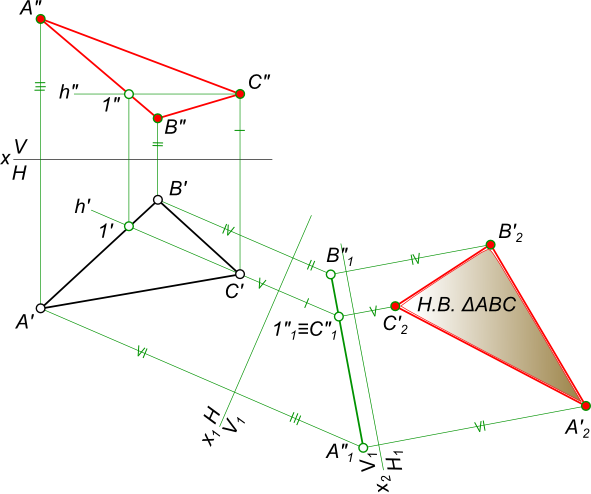
На рисунке 6.26 показано преобразование плоскости общего положения, заданной треугольником АВС, в проецирующую плоскость, которое выполнено одной заменой плоскостей проекций 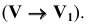
Рассмотренные задачи положены в основу решения многих геометрических задач.
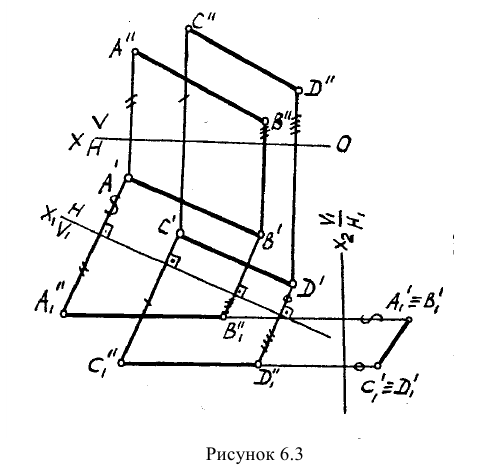
Пример: Определить расстояние между двумя параллельными прямыми АВ и CD (Рис.6.3).
Решение: Расстояние между параллельными прямыми определится, если обе прямые преобразовать в проецирующие. Тогда расстояние между двумя полученными точками будет являться искомым расстоянием. Преобразование произведем двумя заменами
Пример: Определить угол между двумя плоскостями (двугранный угол).
Решение: Двугранный угол определится, если общее ребро угла перевести в проецирующее положение (см. рисунок 6.2а). Тогда ребро «вырождается» в точку, а плоскости — в линии. Угол между линиями является искомым углом (рисунок 6.4).
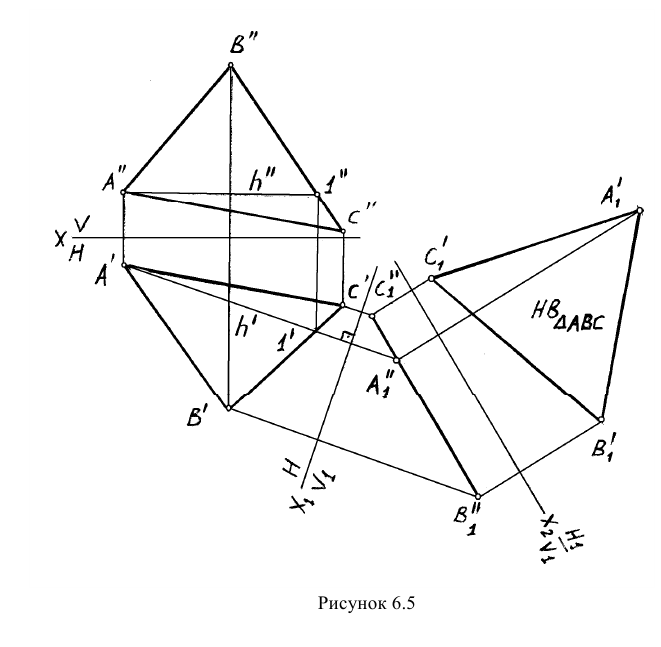
Пример: Определить натуральную величину треугольника АВС.
Решение: Натуральную величину треугольника определим двумя заменами
Сначала треугольник переведем в проецирующее положение, а затем — в параллельное. В последнем положении плоскость треугольника будет параллельна новой плоскости проекций 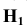
Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Метод вращения вокруг проецирующих осей
Метод заключается в том, что геометрический объект (прямую или плоскость) вращают вокруг проецирующей оси до положения параллельности какой-либо плоскости проекций. В результате вращения геометрический объект проецируется на плоскость проекций в натуральную величину. На рисунке 6.6 в наглядной форме представлено вращение вокруг горизонтально-проецирующей оси (а) и вокруг фронтально-проецирующей оси (б) точки А.
Из приведенных схем видно, что если точка вращается вокруг горизонтально-проецирующей оси, то её горизонтальная проекция перемещается по дуге окружности, а фронтальная — по прямой линии, параллельной оси ОХ. При вращении вокруг фронтально-проецирующей оси наблюдается обратная картина.
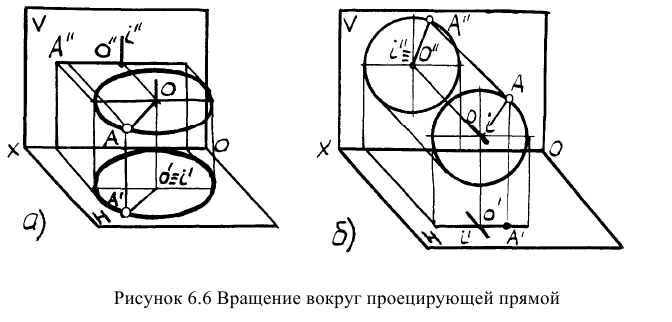
Пример: Определить угол наклона прямой к плоскости проекций Н и натуральную величину прямой.
Решение: НВ прямой и угол 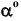
Видео:Эпюр Монжа. Основные принципыСкачать

Вращение вокруг линий уровня (горизонтали или фронтали)
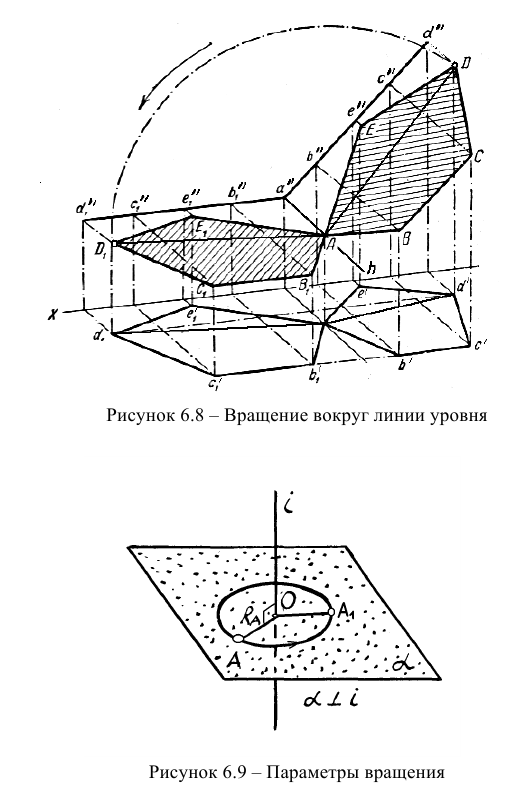
Метод вращения вокруг горизонтали или фронтали заключается в том, что объект, например, плоскую фигуру вращают вокруг горизонтали или фронтали, проведенной в плоскости, до положения параллельности какой-либо плоскости проекций. После окончания вращения объект проецируется на плоскость проекций в натуральную величину (рисунок 6.8).
Главным вопросом метода вращения вокруг линий уровня является вопрос о параметрах вращения. Параметры вращения — это аппарат для решения задач с использованием этого метода.
Параметрами вращения являются (рисунок 6.9):
- Объект вращения. Под объектом вращения следует понимать точку на геометрическом теле. Поэтому в каждой задаче важно определить точки, которые будут вращаться и конечное положение которых надо определить, чтобы получить решение;
- Ось вращения (выбирается произвольно, если не задана);
- Плоскость вращения объекта. Она проводится перпендикулярно оси вращения;
- Центр вращения объекта. Это точка пересечения оси с плоскостью вращения;
- Радиус вращения объекта. Это расстояние между точкой и центром вращения.
- Новое положение объекта вращения (выбирается такое, чтобы геометрический объект занял частное положение).
Конечное положение объекта вращения (на рисунке 6.8, например, точка D) определится, когда радиус вращения (отрезок AD) станет проецироваться на плоскость проекции в натуральную величину.
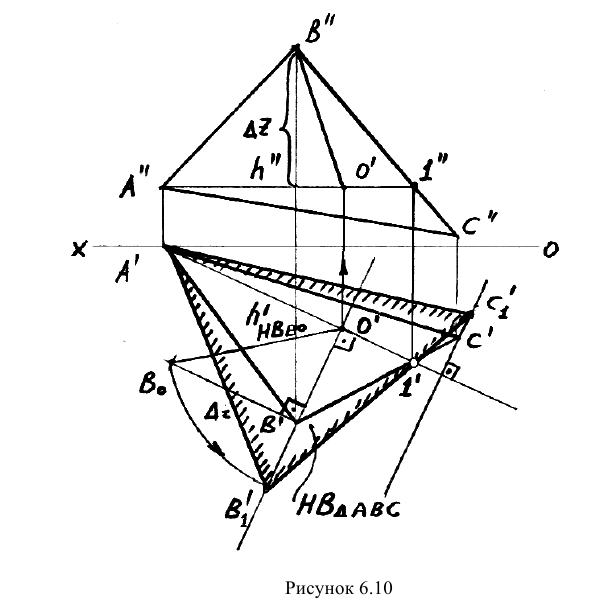
Пример: Определить натуральную величину треугольника АВС методом вращения вокруг горизонтали (рисунок 6.10).
Решение: План решения задачи и его реализация:
1) В плоскости треугольника проводим горизонталь h;
2) Определяем объекты вращения — точки В и С. Точка А не может являться объектом вращения, так как она находится на оси и не будет перемещается в плоскости вращения;
3) Проводим плоскости вращения точек В и С перпендикулярно
4) Начинаем вращать точку, например. В;
5) В месте пересечения плоскости вращения точки В с осью вращения находим центр вращения О
6) Строим проекции радиуса вращения точки В (отрезок ОВ);
7) Находим НВ радиуса вращения ОВ и откладываем его на плоскости вращения точки В отточки
8) Получаем окончательное положение точки после вращения (точка
9) Положение точки С можно найти таким же способом или другим способом, соединив точки 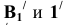
10) Полученные точки соединяем. Треугольник 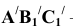
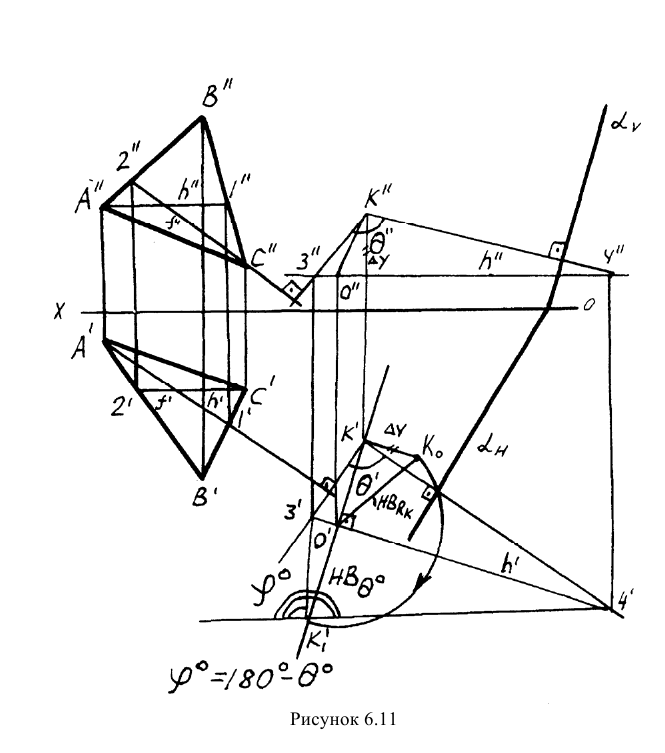
Ранее рассматривался вопрос об определении углов между прямой и плоскостью и между двумя плоскостями (см. раздел «Метрические задачи») с помощью дополнительных углов. Было показано, что натуральную величину дополнительных углов наиболее целесообразно определять методами преобразования, например, методом вращения вокруг горизонтали или фронтали. Рассмотрим пример задачи на определение угла между двумя плоскостями.
Пример: Определить угол между плоскостью треугольника АВС и плоскостью а, заданной следами.
Решение: План решения и его реализация:
- В растворе двугранного угла возьмем любую точку К;
- Из точки К опустим перпендикуляры на обе плоскости (см. тему «Перпендикуляр к плоскости»);
- Между двумя перпендикулярами получаем дополнительный угол
- Определяем натуральную величину дополнительного угла методом вращения вокруг горизонтали h (см. тему «Вращение вокруг линий уровня»);
- Достраиваем полученную натуральную величину дополнительного угла до 180 градусов и получаем искомый угол
(рисунок 6.11).
Видео:Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать

Метод совмещения
Метод совмещения представляет из себя частный случай вращения вокруг линии уровня. За ось вращения в этом случае принимают один из следов плоскости. Сущность метода заключается в том, что плоскость вместе с объектом, находящимся в ней, вращают до совмещения с плоскостью проекций.
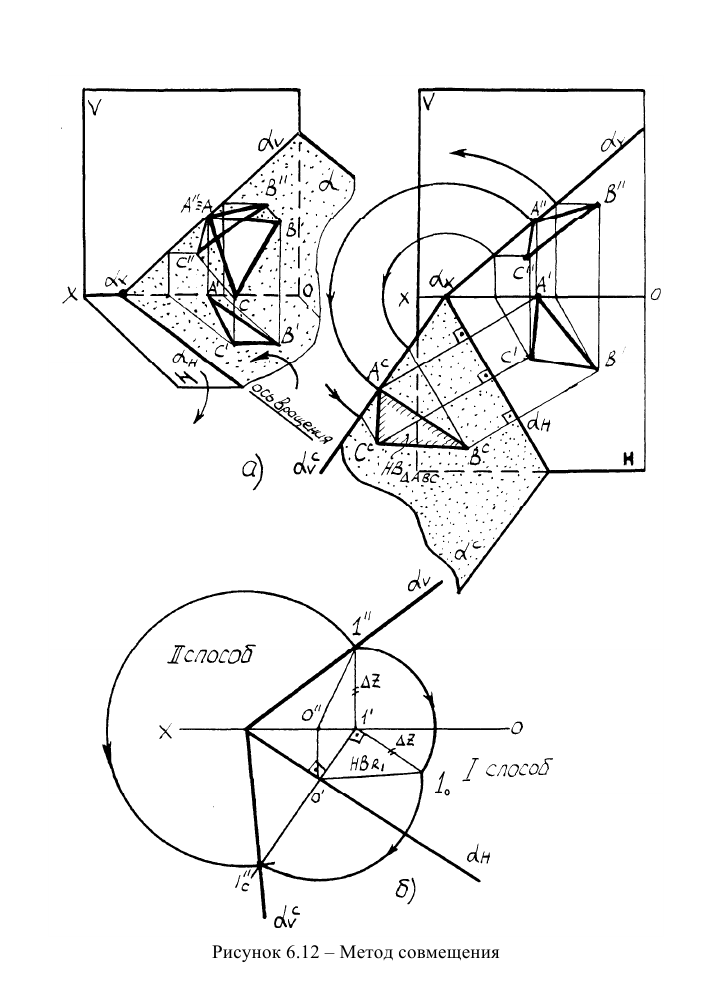
Наглядное изображение способа совмещения вокруг
горизонтального следа представлено на рисунке 6.12. Исходное положение плоскостей проекций и плоскости дано на рисунке 6.12а. После поворота плоскости проекций Н и плоскости а образуется единая плоская система, в которой заданная плоскость вместе с треугольником, принадлежащим этой плоскости, совмещена с плоскостью Н (рисунок 6.12а). Для метода совмещения характерны все параметры вращения, которые рассматривались выше.
Главным вопросом метода совмещения является построение совмещенного следа 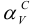
Пример: Найти натуральную величину треугольника AВС, принадлежащего плоскости а.
Решение: С помощью точки А, принадлежащей фронтальному следу, найдем совмещенный фронтальный след 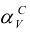
Точка С треугольника находится на горизонтальном следе плоскости и поэтому не будет вращаться (горизонтальный след плоскости — ось вращения). Через точку В треугольника проведем горизонталь h и точку 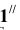
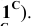
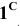
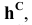
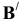
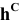
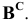
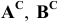
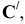
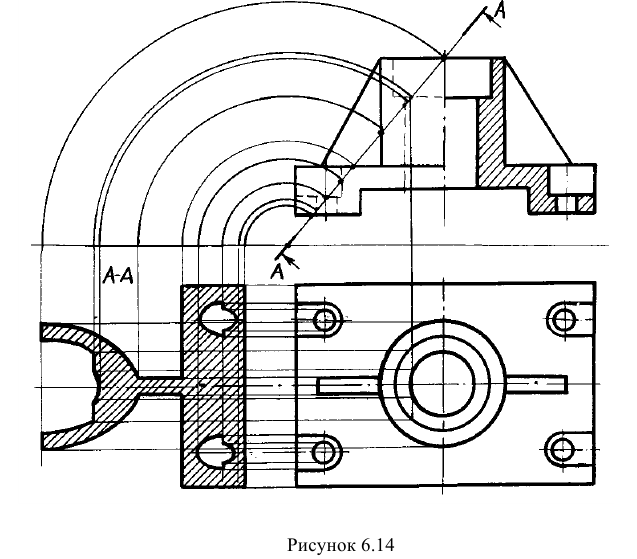
Пример: Методом совмещения построить наклонное сечение детали.
Решение: Секущая плоскость А-А в данном случае является фронтально проецирующей. Совмещение осуществлялось вращением вокруг горизонтального следа, который перпендикулярен горизонтальной оси проекций (рисунок 6.14).
Видео:Как начертить Эпюр 1 КНИТУ(КХТИ) 1 курс.Найти расстояние от точки D до плоскости треугольника ABCСкачать

Метод плоско-параллельного перемещения
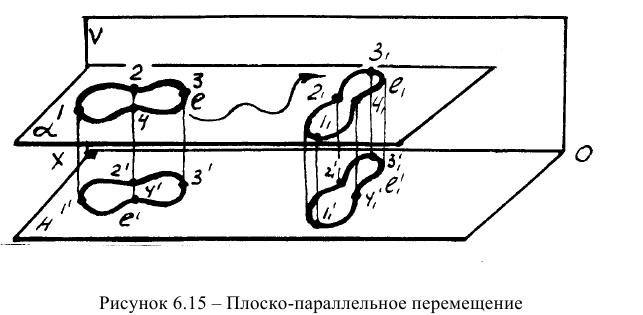
Плоско-параллельное перемещение — это вид механического движения объекта, когда каждая его точка перемещается в плоскости, параллельной какой-либо плоскости проекций, в результате чего объект перемещается на новое место и ему придаётся новое положение (рисунок 6.15).
Различают плоско-параллельное перемещение относительно плоскости Н — ППП(Н) и относительно плоскости V — ППП(У).
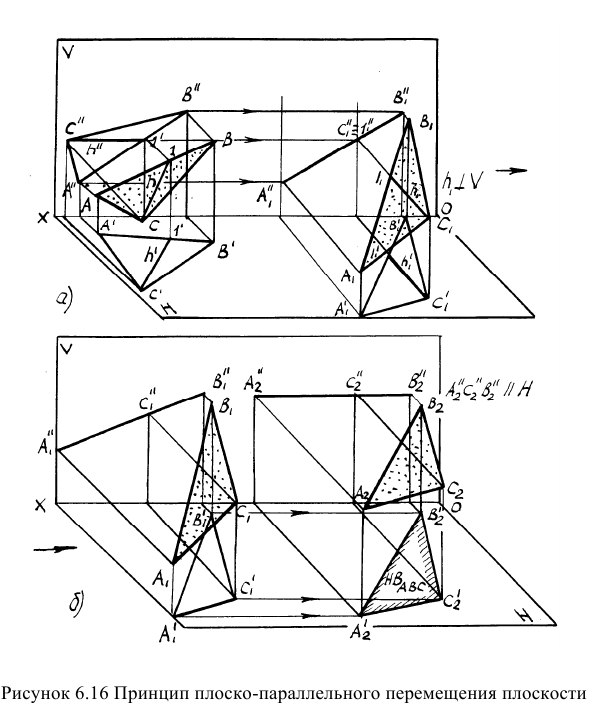
При плоско-параллельном перемещении объекта относительно плоскости Н горизонтальная проекция объекта изменяет свое положение, не изменяя своей формы и размеров. Фронтальная проекция объекта при этом изменяется по форме и размерам, а каждая точка объекта перемещается по прямым линиям, параллельным оси ОХ. ППП(Н) показано на рисунке 6.16а. Обратная картина наблюдается при ППП(V) -рисунок 6.166.
Оба вида плоско-параллельного перемещения, представленные на рисунке, применяются при решении типовых задач на определение натуральной величины плоских фигур.
Для решения задачи по определению натуральной величины отрезка прямой общего положения необходимо сделать одно перемещение и разместить одну из проекций так, чтобы она стала параллельна оси ОХ.
Для решения задачи на определение натуральной величины плоскости совершают два плоско-параллельных перемещения: сначала относительно одной плоскости проекций, а затем относительно другой.
Целью первого перемещения является перевод плоскости из общего положения в проецирующее. Плоскость станет проецирующей, если будет содержать прямую, перпендикулярную плоскости проекций. В качестве такой прямой используют горизонталь или фронталь. При первом перемещении проекция натуральной величины горизонтали или фронтали плоскости должна принять положение, перпендикулярное оси ОХ. Целью второго перемещения является перевод плоскости из проецирующего положения в положение, параллельное плоскости проекции. После этого плоскость проецируется в натуральную величину.
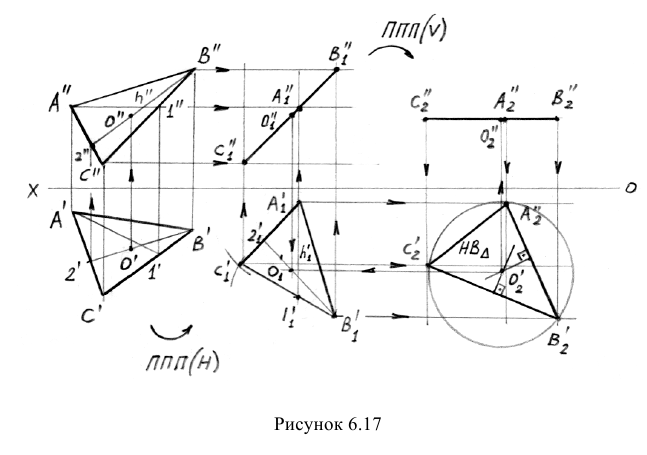
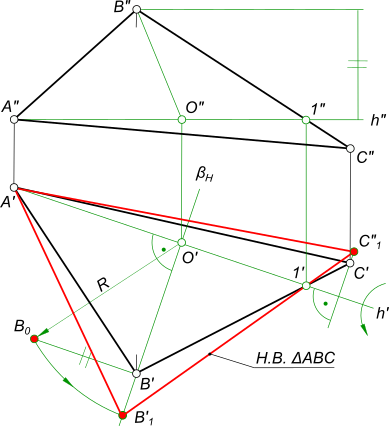
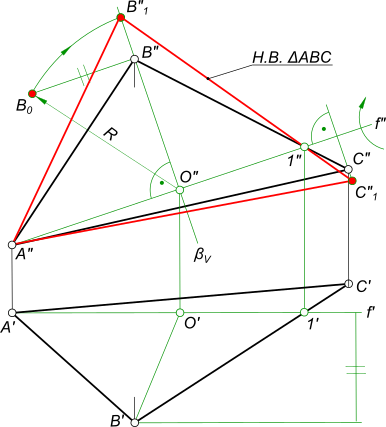
Пример: Методом плоско-параллельного перемещения определить центр окружности, описанной вокруг треугольника AВС.
Решение: Для того, чтобы найти центр описанной окружности треугольника, необходимо определить его натуральную величину. На основании вышерассмотренного материала совершим два плоскопараллельного перемещения: ППП(Н) и ППП(V) (рисунок 6.17).
Для преобразования плоскости треугольника во фронтально-проецирующую плоскость проведем в треугольнике горизонталь h и расположим её при первом ППП перпендикулярно оси ОХ. На ней построим треугольник 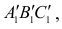
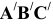
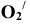
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Касательные плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Проецирование прямой линии
- Проецирование плоскости
- Плоскость на эпюре Монжа
- Позиционные задачи
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Построить натуральную величину треугольника авс
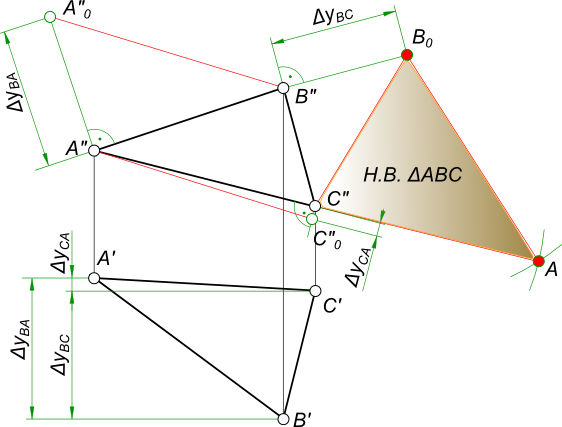
Натуральная величина треугольника на эпюре Монжа может быть определена: – способом прямоугольного треугольника;
Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.
Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:
– Способ вращения вокруг осей перпендикулярных плоскостям проекций;
– Вращение вокруг горизонтали представляющих собой линии уровня;
представляющих собой линии уровня;
– Вращение вокруг следа или способ совмещения с плоскостью проекций;
Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.
Ниже приведены решения одной и той же задачи вышеописанными методами.
9.6.1. Задание:определить натуральную величину треугольника ABC(рис. 9.8), а также угол наклона плоскости треугольника к плоскости П1.
1) Решение методом замены плоскостей проекций (рис. 9.9).

Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A1B1C1 проводят ось x1,4новой системы плоскостей проекций П1/П4перпендикулярно к горизонтальной проекции горизонтали h1.В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П4.
На линиях проекционной связи в новой системе откладывают координатыzточек А, В, С с фронтальной проекции исходной системы плоскостей П1/П2.
При соединении новых проекций А4,B4, С4получают прямую линию, в которую спроецировался треугольник ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П1 – угол α. На чертеже это угол между осью x1,4и проекцией С4А4В4.
Второй этап. Выбираем новую плоскость проекции П5,параллельную плоскости треугольника, т.е. новую ось x4,5проводят параллельно С4А4В4на произвольном расстоянии. Получают новую систему П4/П5.Полученный треугольник А5В5С5и есть искомая натуральная величина треугольника ABC.
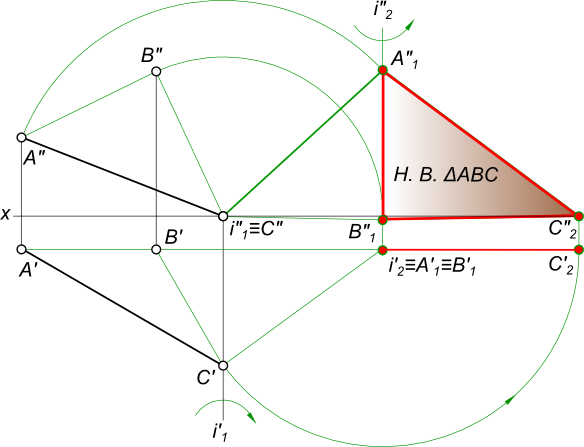
2) Решение методом вращения вокруг проецирующей оси(рис. 9.10).
Задача решается в два этапа. На первом этапе выполняют вращение так, чтобы плоскость треугольника ABCпреобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плоскостей проекций. Для этого проводят горизонталь h (h1,h2) через точку А. (построение начинают с фронтальной проекции h2,она проходит через проекцию точки A2и проекцию точки 12 при этомh2 параллельна оси х).Далее находят горизонтальную проекцию h1 горизонтали h (через проекции A1 и 11). Через точку А проводят ось i – ось вращения треугольника так, чтобы она была перпендикулярна к П1. На фронтальной проекции через вершины А2 и В2 проводят следы горизонтальных плоскостей уровня Δ и Σв которых при вращении будут перемещаться точки АиВ. Вершина С принадлежит плоскости П1поэтому ее плоскостью вращения будет плоскость проекций П1.На горизонтальной проекции, взяв за центр вращения проекцию i1 поворачивают горизонталь А так, чтобы на плоскость П2 она спроецировалась в точку. На чертеже это выразится 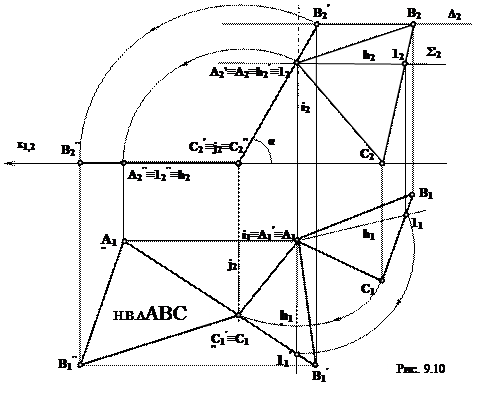
При этом на фронтальной проекции А2 остается неизменной, находясь на следе плоскости Σ2 и ее обозначим a2‘.
На горизонтальной проекции поворачиваем оставшиеся вершины В и С вокруг оси i так, чтобы 

На втором этапе проводят ось jчерез вершинуС так, чтобы ось была фронтально проецирующая. При этом С’2 ≡ j’2, а горизонтальная проекция j’1 пройдет через проекцию С’1. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А’2 и В’1, вокруг j2 до совмещения с осью х,при этом проекции B’1 и A’1 будут перемещаться параллельно оси хи займут новое положение В»1, и А»1 вершина С останется на месте. Соединив точки между собой, получают новое положение плоскости (оно соответствует натуральной величине треугольника ABC).
3) Решение методом плоскопараллельного перемещения (рис. 9.11).
Задача решается в два этапа. На первом этапе преобразуют чертеж так, чтобы плоскость треугольника ABC стала перпендикулярна к одной из плоскостей проекций. Для этого проводят в плоскости треугольника горизонталь h (фронтальная проекция А212║х,). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П1. В рассматриваемом примере вершина С принадлежит плоскости проекций П1, А принадлежит плоскости Σ, В — плоскости Δ.
Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h1 треугольника не станет перпендикулярна к фронтальной плоскости проекций П2.
Для этого на свободном поле чертежа вычерчивают горизонтальную проекцию треугольника A1 ′ B1 ′ C1 ′ с условием, чтобы А111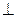
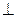
На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А2‘В2‘С2‘располагают на произвольном расстоянии от оси хпараллельно плоскости П1. При этом вершины А, Ви С треугольника заключают в горизонтально проецирующие плоскости θ, Т, Р. По следам этих плоскостей будут перемещаться горизонтальные проекции вершин А1‘В1‘С1‘. От нового положения фронтальной проекции А2«В2«С2« проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (θ1,T1,P1), и получая проекции точек А1» В1» C1«. Соединив эти проекции, получают треугольник ABC в натуральную величину.
4) Решение методом вращения вокруг линии уровня(рис.9.12)
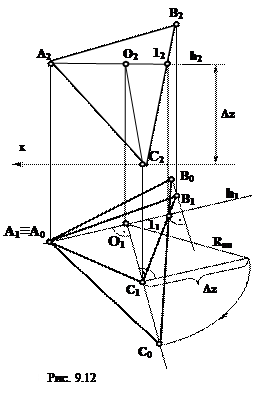
Для определения натуральной величины радиуса вращения используют любой метод (в данном случае способ прямоугольного треугольника) строят прямоугольный треугольник, в котором O1C1 – один из катетов. Второй катет – разность координат Δzотрезка О2С2, взятого с фронтальной проекции. В построенном треугольнике гипотенуза O1C – натуральная величина радиуса вращения.
На продолжении перпендикуляра O1C1 откладывают |RBp.| и получают новое положение вершины С после вращения — С . Проекция вершины В получается пересечением луча C 11 и перпендикуляра к горизонтальной проекции h1 проведенного через проекцию точки В1.
Треугольник A B C есть искомая натуральная величина треугольника ABC.
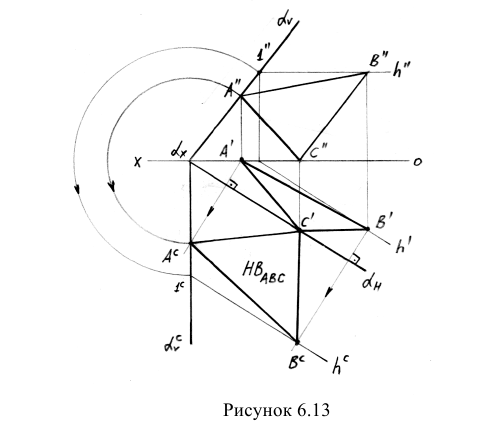
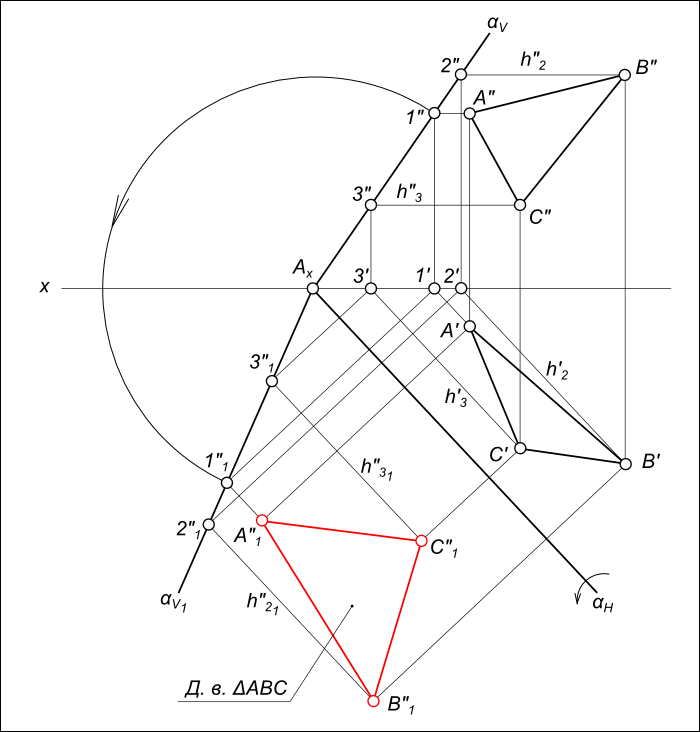
5) Решение методом совмещения(рис. 9.13).
Для решения задачи методом совмещения необходимо построить следы плоскости Σ, которой принадлежит треугольник ABC. Для этого проводят в плоскости треугольника ABC фронталь f и находят горизонтальный след этой фронтали – N1. По условию задачи вершина С треугольника принадлежит горизонтальной плоскости проекций П1. Тогда горизонтальный след Σ1 плоскости Σпроводят через проекции N1 и C1. Соединив эти две точки и продлив отрезок до пересечения с осью х, находят точку схода следов Σх. Учитывая, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след Σ2 плоскости Σпроводят через точку Σхпараллельно проекции фронтали f2.
Для нахождения натуральной величины треугольника ABCнеобходимо построить совмещенное положение плоскости Σ с горизонтальной плоскостью проекций П1. Для этого через вершину Апроводят горизонталь h1. На фронтальном следе Σ2 фиксируют точку 22. Ее горизонтальная проекция – точка 21. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости Σ. Поэтому, чтобы построить точку 2 в совмещенном положении 2 , проводят из 21перпендикуляр к горизонтальному следу Σ, а из центра Σх дугу окружности радиусом Σх22 до пересечения с направлением перпендикуляра. Соединив Σх с 2 , получают совмещенное положение фронтального следа Σ – Далее через точку 2 проводят горизонталь h всовмещенном положении. На этой горизонтали находят точку А , проведя перпендикуляр из точки A1 к горизонтальному следу Σ1.
По такой же схеме строят совмещенное положение точки В . Совмещенное положение точки С совпадает с ее горизонтальной проекцией С1 т.е. С1≡С . Соединив построенные точки, получают треугольник А В С – это и есть натуральная величина треугольника ABC.
Не нашли то, что искали? Воспользуйтесь поиском:
Метки
Видео:Лекция №3. Эпюр Монжа.Скачать

Натуральная величина треугольника с описанием.
Натуральная величина треугольника определяется 2 методами:
- замена плоскостей проекции;
- плоскопараллельное перемещение.
Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».
Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.
Алгоритм определения натуральной величины плоскости:
Замена плоскостей проекции
1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.
2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.
3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:
- от С2 до оси Х;
- от В2 до оси Х;
- от А0 до оси Х.
Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.
4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.
5.) Отмеряются расстояния:
- от В1 до Х1;
- от С1 до Х1;
- от А1 до Х1.
Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

Плоскопараллельное перемещение
7.) Откладывается отрезок на оси Х (обозначен синим цветом).
8.) Переносятся точки на текущее построение.
9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 


Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).




🎦 Видео
Сдача зачета по начертательной геометрии МГСУ-МИСИСкачать

Построение точек по координатамСкачать

Проецирование точкиСкачать

Построение следов плоскостиСкачать

Проецирование прямой общего положенияСкачать

Определение длины отрезкаСкачать

Определение видимости.Скачать

Проецирование точки на 3 плоскости проекцийСкачать

2 3 проекция точки на конусеСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Пересечение прямой и плоскостиСкачать

Построение треугольника в трёх проекцияхСкачать

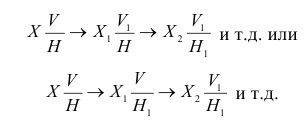
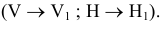
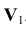 . Для того, чтобы построить новую фронтальную проекцию точки на новой плоскости проекций
. Для того, чтобы построить новую фронтальную проекцию точки на новой плоскости проекций 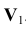
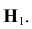 Для того, чтобы построить новую горизонтальную проекцию точки на новой плоскости проекций
Для того, чтобы построить новую горизонтальную проекцию точки на новой плоскости проекций 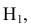 необходимо от новой оси по новой линии связи отложить ординату точки из предыдущей системы плоскостей проекций.
необходимо от новой оси по новой линии связи отложить ординату точки из предыдущей системы плоскостей проекций.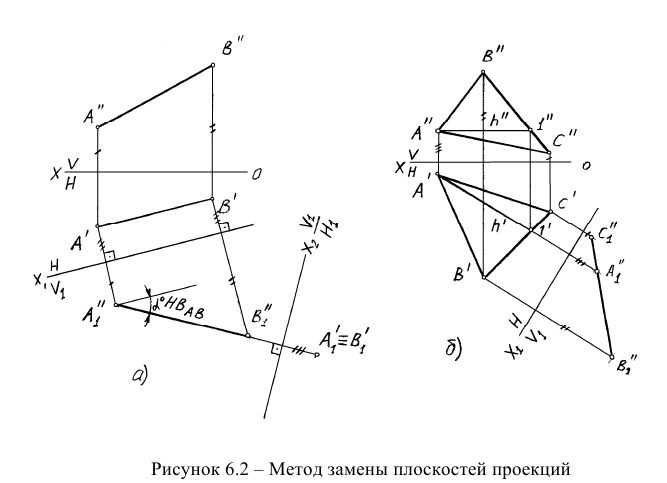
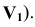
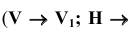
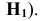
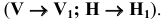
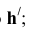
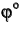 (рисунок 6.11).
(рисунок 6.11).