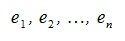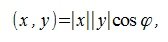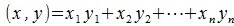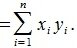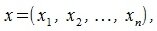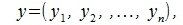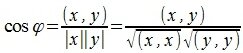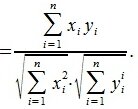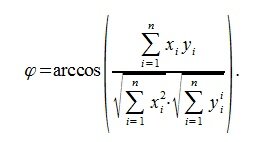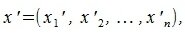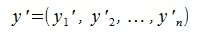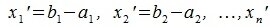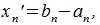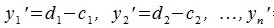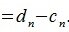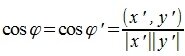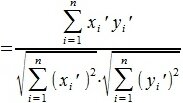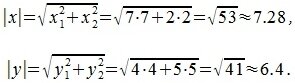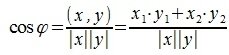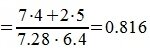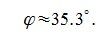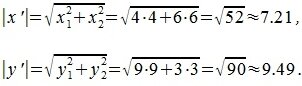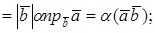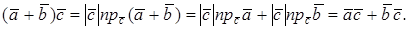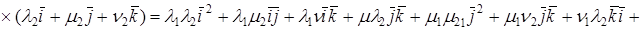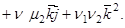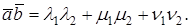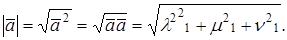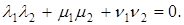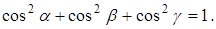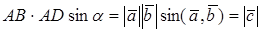Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.
- Калькулятор для вычисления угла между векторами
- Инструкция использования калькулятора для вычисления угла между векторами
- Ввод даных в калькулятор для вычисления угла между векторами
- Дополнительные возможности калькулятора для вычисления угла между векторами
- Теория. Вычисление угла между векторами
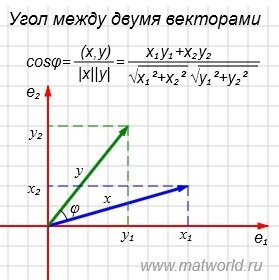
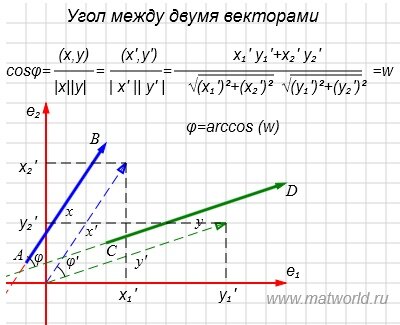
- Угол между двумя векторами
- Примеры вычисления угла между двумя векторами
- УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
- 🎥 Видео
Видео:Как находить угол между векторамиСкачать

Калькулятор для вычисления угла между векторами
Инструкция использования калькулятора для вычисления угла между векторами
Ввод даных в калькулятор для вычисления угла между векторами
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления угла между векторами
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Видео:Угол между векторами | МатематикаСкачать

Теория. Вычисление угла между векторами
Угол между двумя векторами a и b можно найти использовав следующую формулу:
| cos α = | a · b |
| | a || b | |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Угол между двумя векторами
Пусть в n-мерном пространстве задан ортонормированный базис
Как известно скалярное произведение ненулевых векторов x и y называется произведение
Если x=0 или y=0, то скалярное произведение равно нулю.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения
координаты векторов x и y соответственно.
Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен
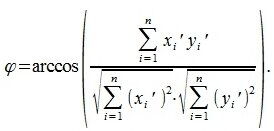
И, следовательно, угол между двумя векторами будет равен
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x= AB и y= CD, где 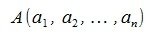
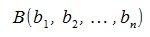
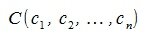
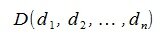
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
При таком перемещении угол между векторами x и y равен углу между векторами x’ и y’. Следовательно косинус угла между двумя векторами равен:
Угол между двумя векторами будет равен:
Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Примеры вычисления угла между двумя векторами
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пример . Найти угол между векторами x=(7,2) и y=(4,5).
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).
Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:
Косинус угла между векторами x и y, будет равен:
Из выражения (5) вычисляем угол φ:
Вариант 2. Начальные точки векторов произвольные.
Пример . Найти угол между векторами x= AB и y= CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x= AB и y= CD.
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками): x’=(3-(-1),7-1)=(4,6), y’=(12-3,5-2)=(9,3).
Угол φ между векторами x и y равен углу φ’ между векторами x’ и y’. Поэтому вычисляя угол φ’ , получим угол между векторами x и y.
Вычислим норму векторов x’ и y’:
Косинус угла между векторами x’ и y’:
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
ДОКАЗАТЕЛЬСТВО СВОЙСТВ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Свойство первое следует из определения скалярного произведения: 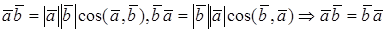
Второе и третье свойства следуют из линейных свойств проекции вектора на ось (направление): 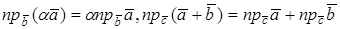
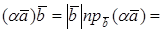
СКАЛЯРНЫЙ КВАДРАТ
Скалярным квадратом называется скалярное произведение 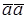
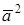
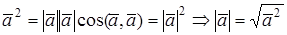
УГОЛ МЕЖДУ ВЕКТОРАМИ
Из определения 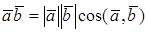
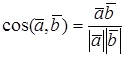
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
Теорема. Векторы 

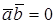
Доказательство необходимости. Пусть 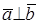
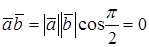

Доказательство достаточности. Пусть 
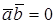
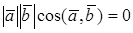
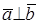
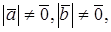
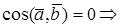
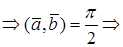
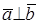
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Теорема. В ортонормированном базисе скалярное произведение векторов 

Доказательство. Пусть в пространстве выбран ортонормированный базис 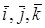


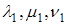

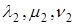
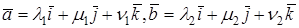
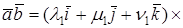
Так как 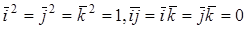
МОДУЛЬ ВЕКТОРА В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Из формулы для скалярного произведения при 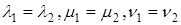
УГОЛ МЕЖДУ ВЕКТОРАМИ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
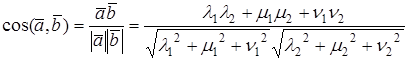
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ В
Если 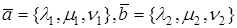
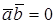
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Определение. Направляющими косинусами вектора 

Пусть 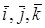
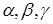

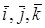
Направляющими косинусами вектора 

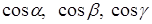
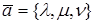
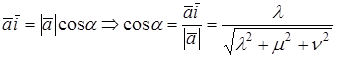
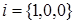
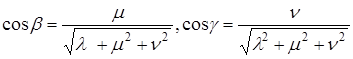
Замечание. Для любого вектора 
ЛИНЕЙНЫЕ СВОЙСТВА ПРОЕКЦИИ ВЕКТОРА НА ОСЬ
В ортонормированном базисе координаты вектора равны проекциям этого вектора на направления соответствующих базисных векторов.
Действительно, если 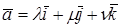
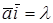
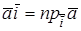
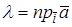
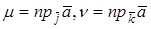
Если 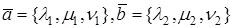
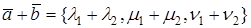
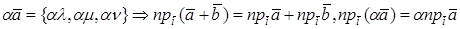
1. Дайте определение скалярного произведения векторов.
2. Выведите условие ортогональности двух векторов.
3. Докажите формулу скалярного произведения векторов в ортогональном базисе.
4. Напишите формулу модуля вектора в ортонормированном базисе.
5. Выведите условие ортогональности двух векторов в ортогональном базисе.
§6. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным произведением вектора 

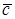
1. 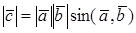
2. 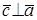
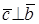
3. Упорядоченная тройка векторов 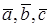
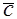
Векторное произведение 

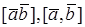
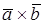
 D C D C 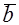 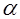 A A  B Рис. 15. B Рис. 15. |      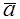  Рис. 14. Рис. 14. |
Замечания. 1. Модуль 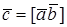


Векторы 

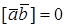
СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. 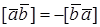
2. 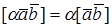
3. 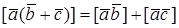
Это свойство примем без доказательства.
ДОКАЗАТЕЛЬСТВО СВОЙСТВ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. Пусть 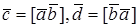
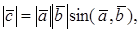
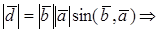
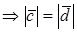
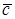
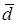


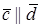
По определению с конца вектора 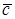


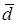


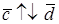
Следовательно, имеем, что 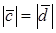
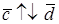
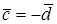
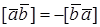
   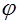 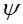 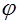 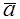 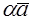 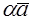 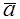 Рис. 16. Рис. 16. |
2. Пусть 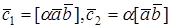
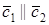
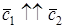
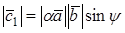
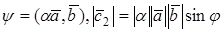
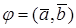
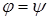
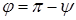
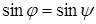
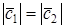
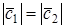
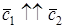
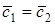
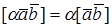
🎥 Видео
Задача 3. Найти косинус угла между векторами.Скачать

Угол между векторами. 9 класс.Скачать

Косинус угла между векторами. Коллинеарность векторовСкачать

11 класс, 5 урок, Угол между векторамиСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Вывод формулы скалярного произведения векторов, заданных координатами в ортонормированном базисе.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

§7 Направляющие косинусы вектораСкачать

100 тренировочных задач #135 Угол между векторамиСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

найти угол между единичными векторамиСкачать

§48 Ортонормированный базис евклидова пространстваСкачать

Скалярное произведение векторов. 9 класс.Скачать