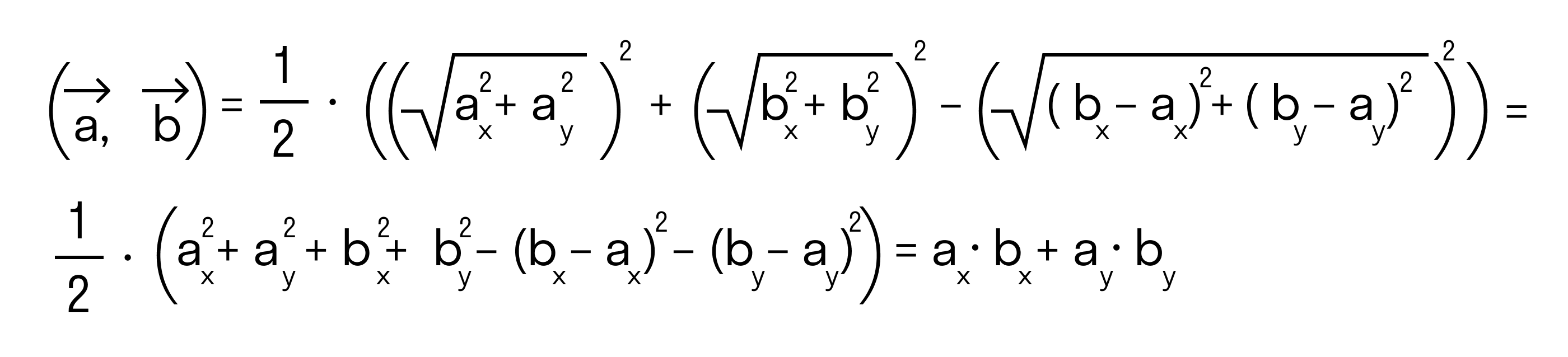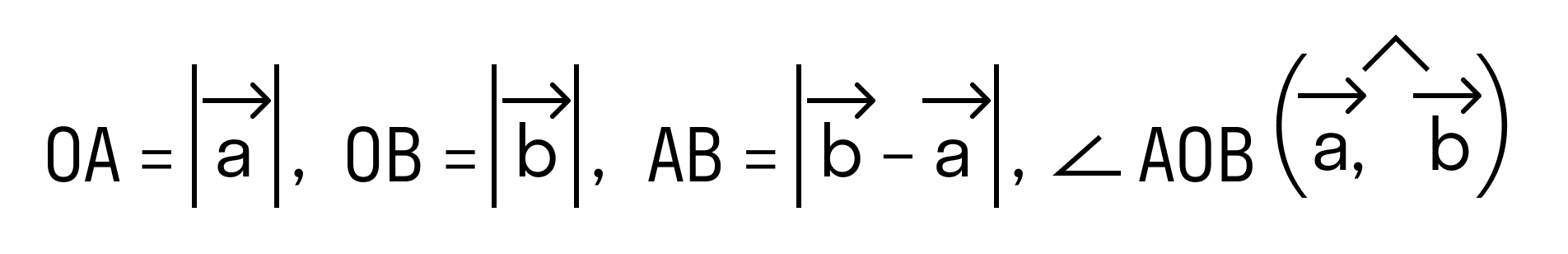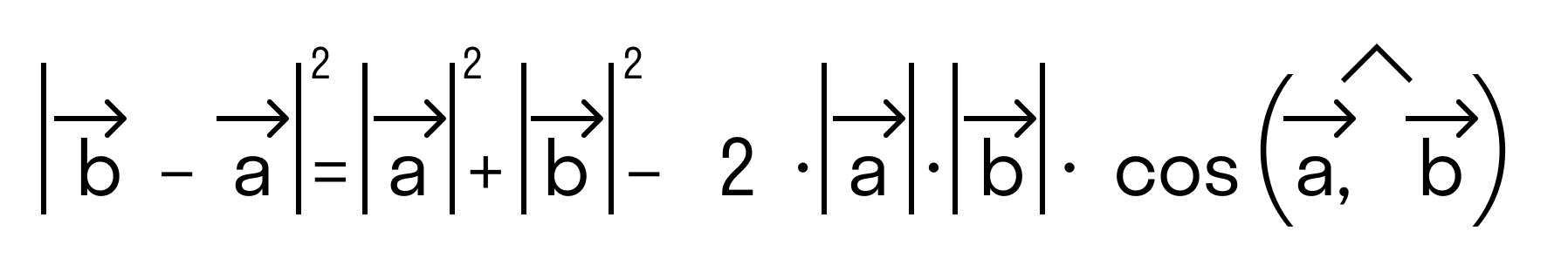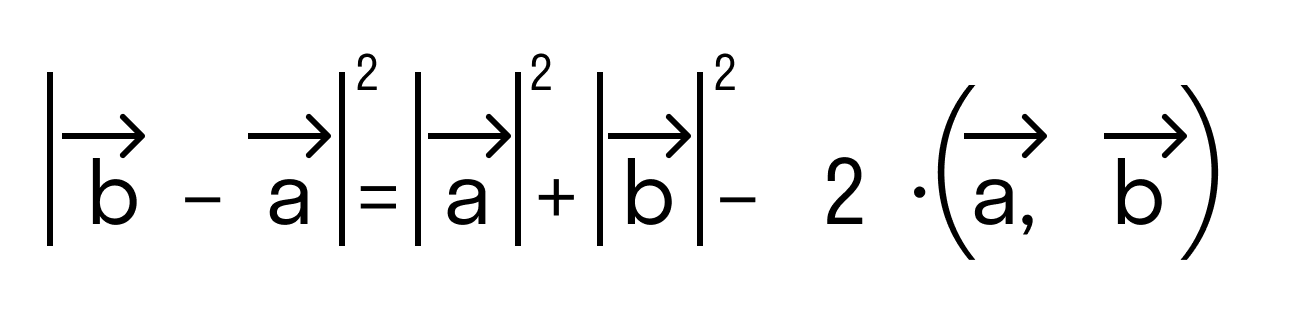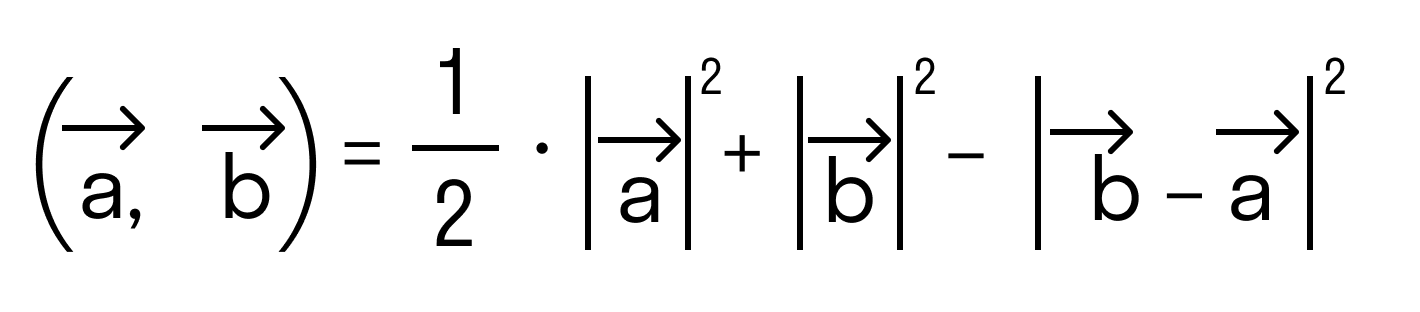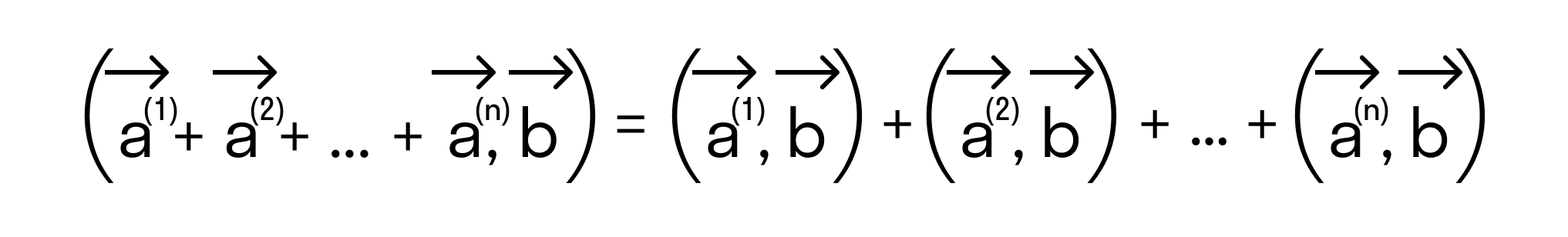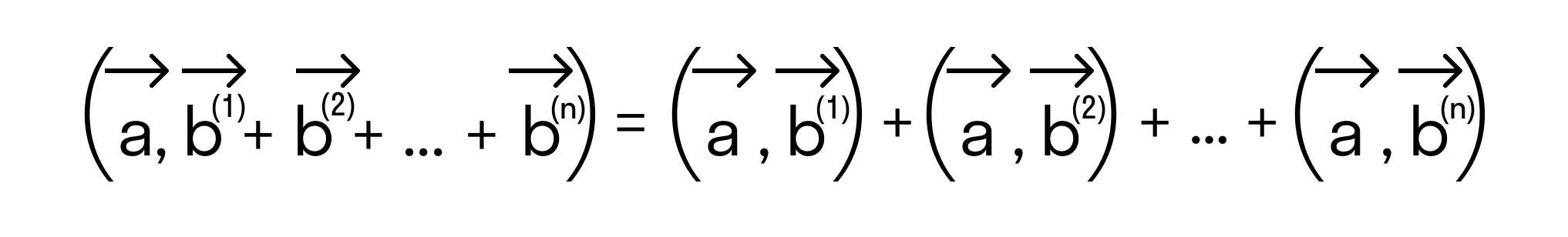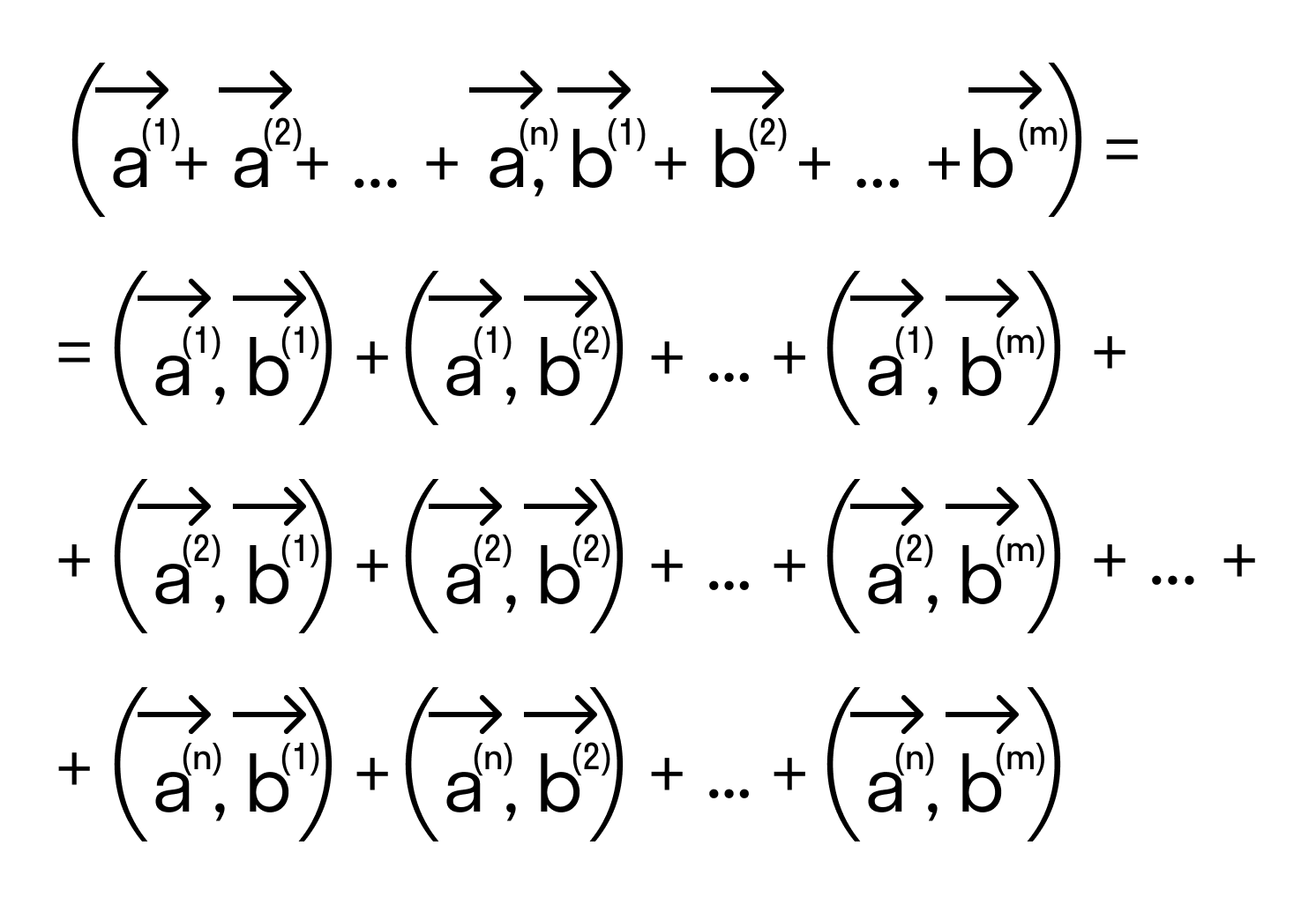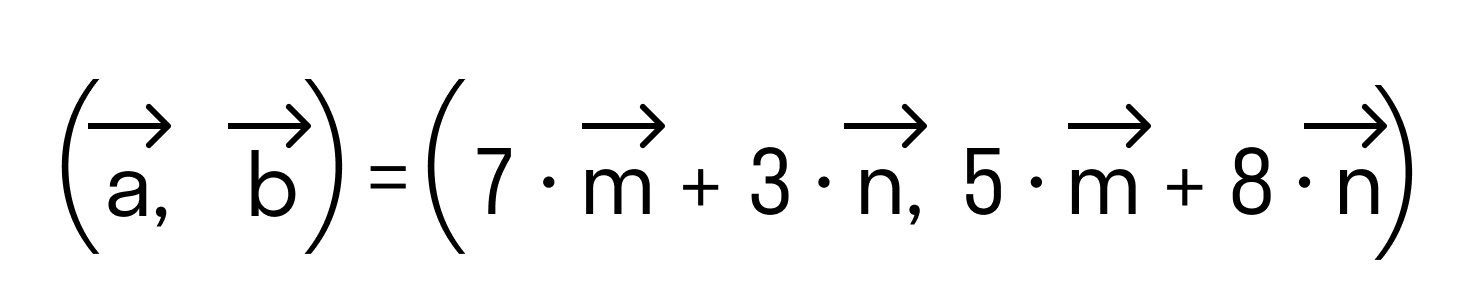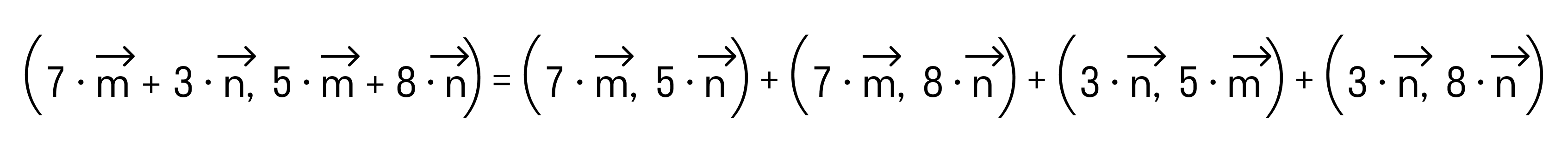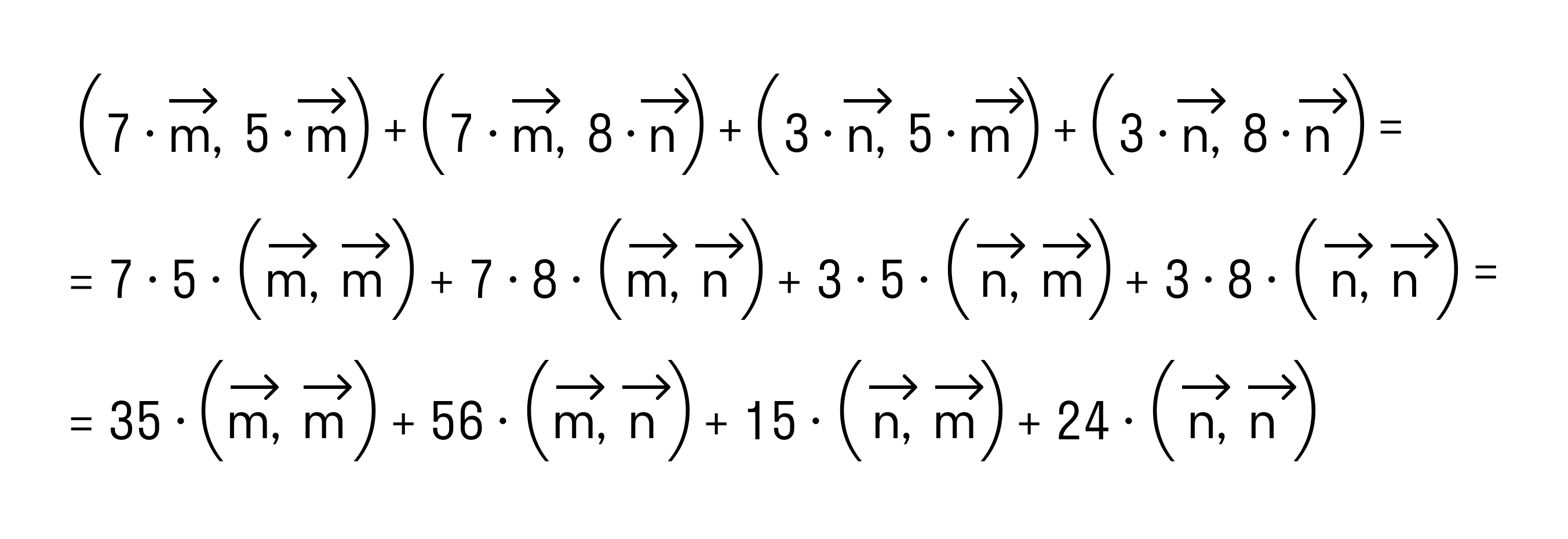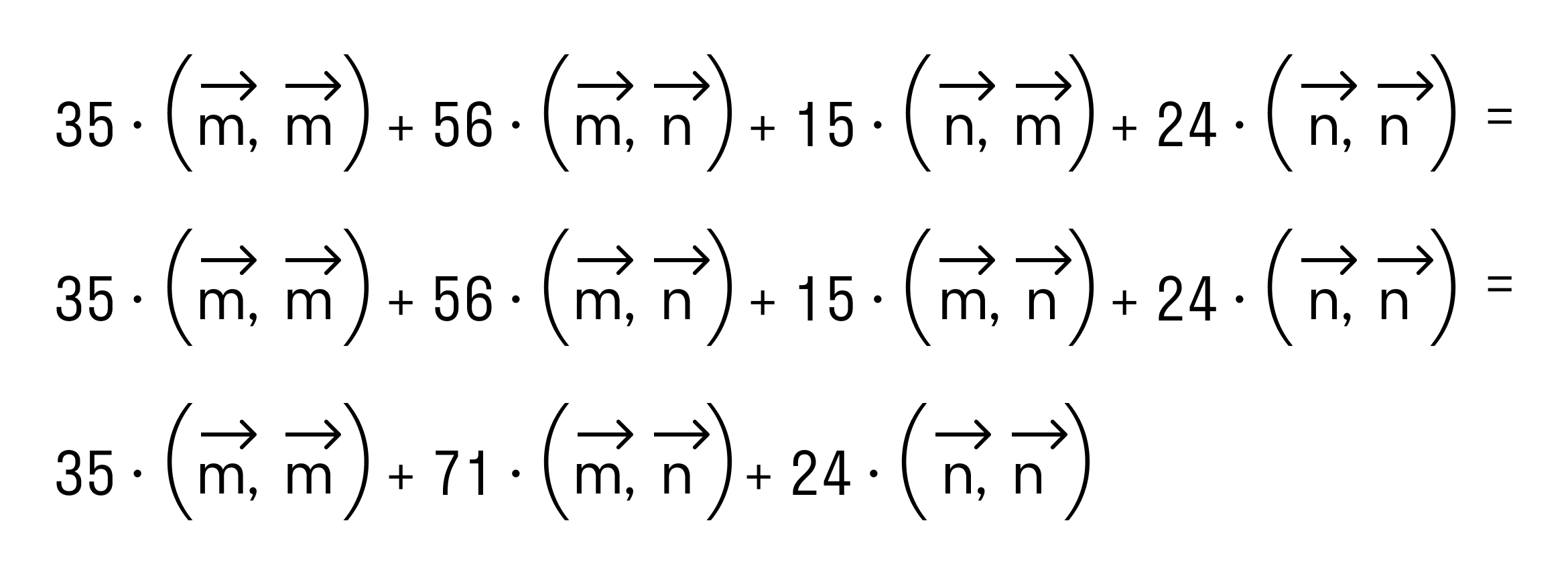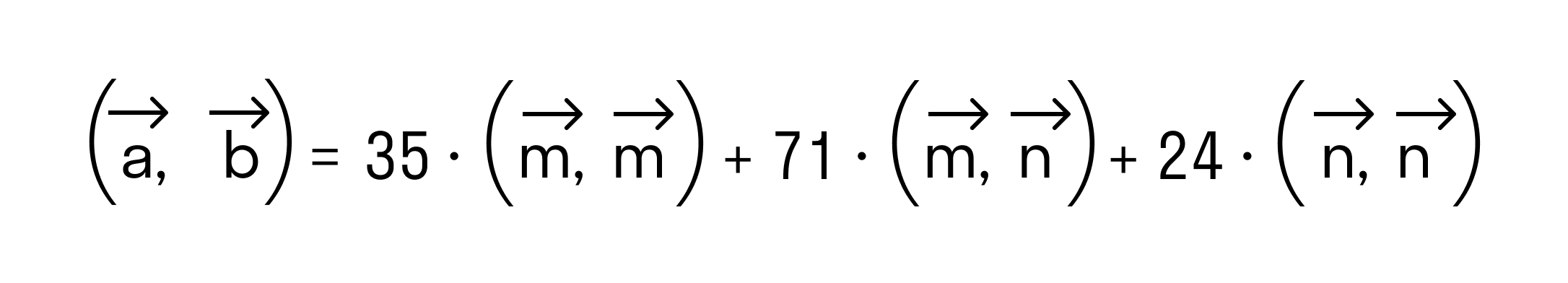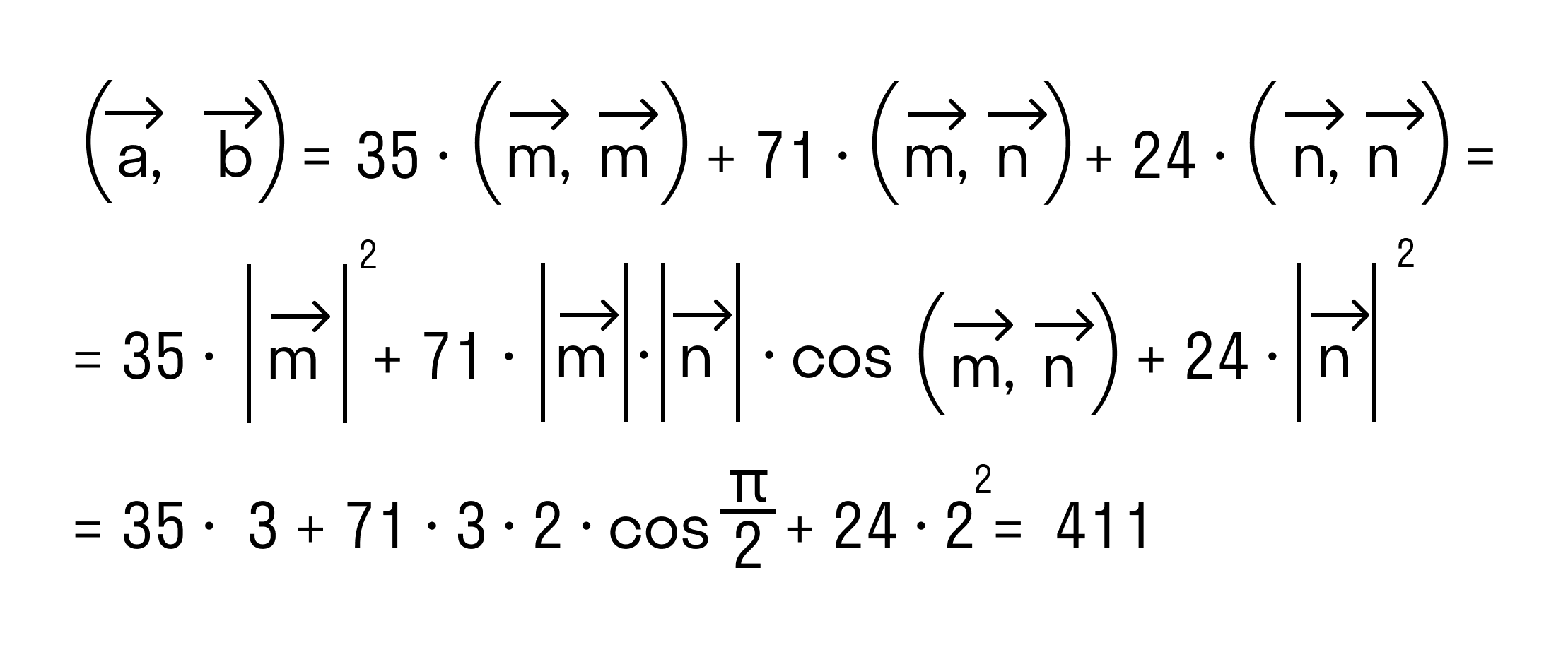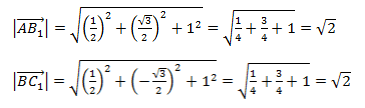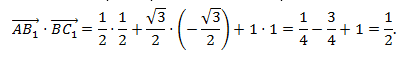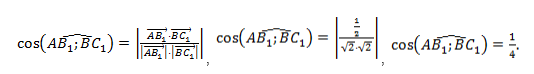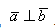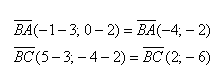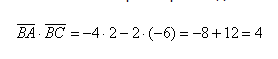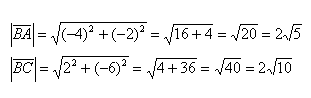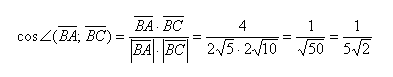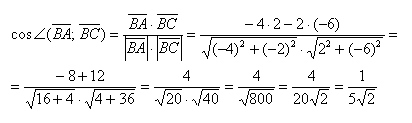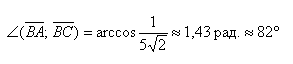Если прямые параллельны то косинус между ними

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

,

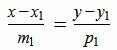(1.1)

,

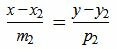(1.2)

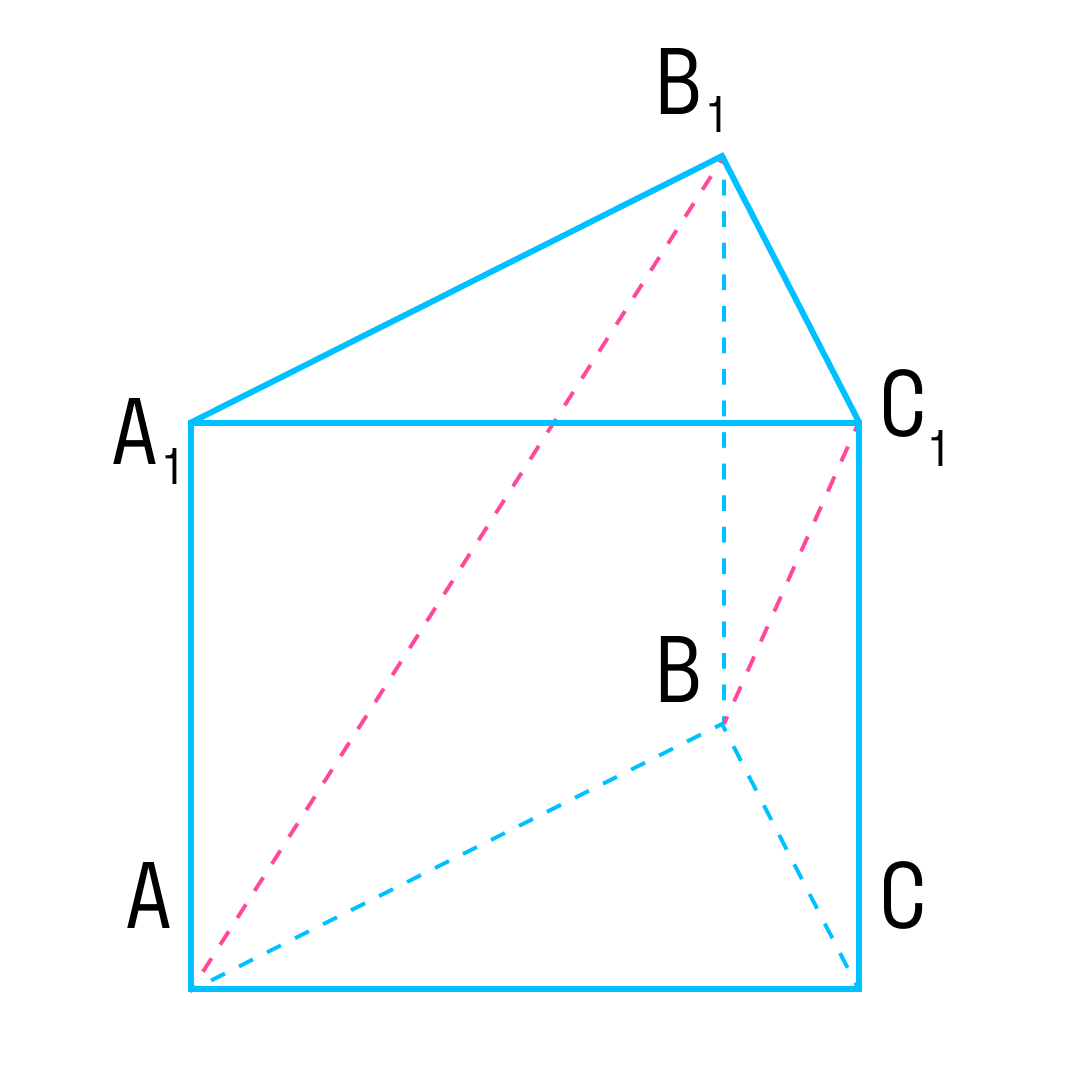
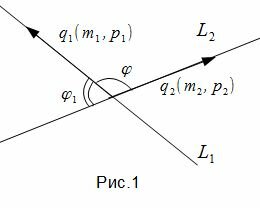
Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

,

,

(1.3)

Из выражения (1.3) получим:

.

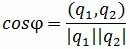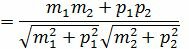(1.4)

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

.

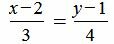(1.5)

.

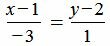(1.6)

.

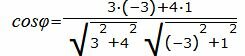Упростим и решим:

.

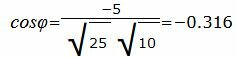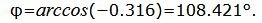Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

.

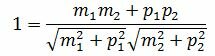(1.7)

Сделаем преобразования с выражением (1.7):

,

,

,

,

,

.

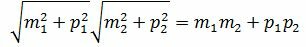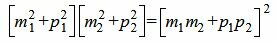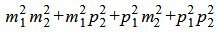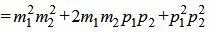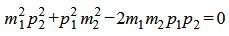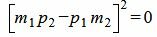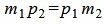(1.8)

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

.

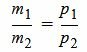(1.9)

Пример 2. Определить, параллельны ли прямые

.

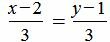(1.10)

.

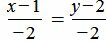(1.11)

, .

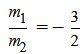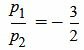Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

.

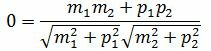(1.12)

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

.

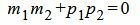(1.13)

Пример 3. Определить, перпендикулярны ли прямые

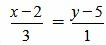(1.14)

.

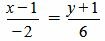(1.15)

.

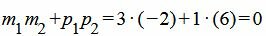(16)

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

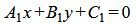(1.17)

.

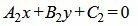(1.18)

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

.

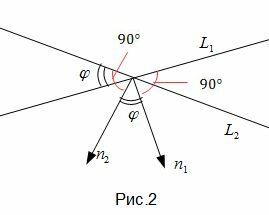Из определения скалярного произведения двух векторов, имеем:

.

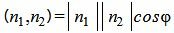(1.19)

Из уравнения (19) получим

.

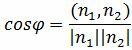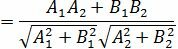(1.20)

Пример 4. Найти угол между прямыми

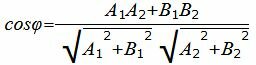(23)

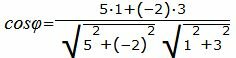Упростим и решим:

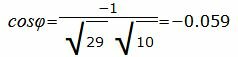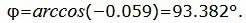Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

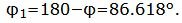1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

.

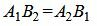(1.24)

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

.

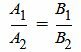(1.25)

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

,

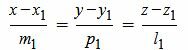(2.1)

,

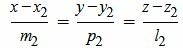(2.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

,

(2.3)

Из выражения (2.3) получим:

.

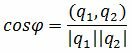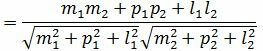(2.4)

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

.

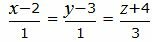(2.5)

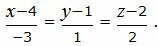(2.6)

.

.

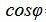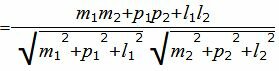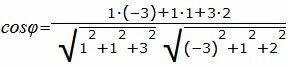Упростим и решим:

.

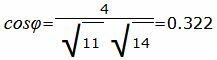Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

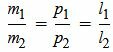(2.8)

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

.

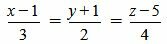(2.9)

.

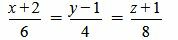(2.10)

, , .

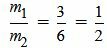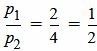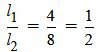Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

.

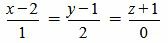(2.11)

.

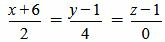(2.12)

.

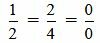(2.13)

Выражение (2.13) нужно понимать так:

, , .

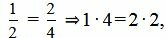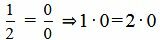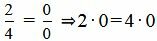(2.14)

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

.

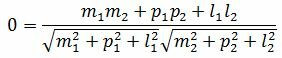(2.15)

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

.

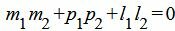(2.16)

Пример 3. Определить, перпендикулярны ли прямые

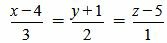(2.17)

.

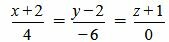(2.18)

.

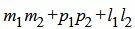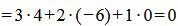(2.19)

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Скалярное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Угол между векторами

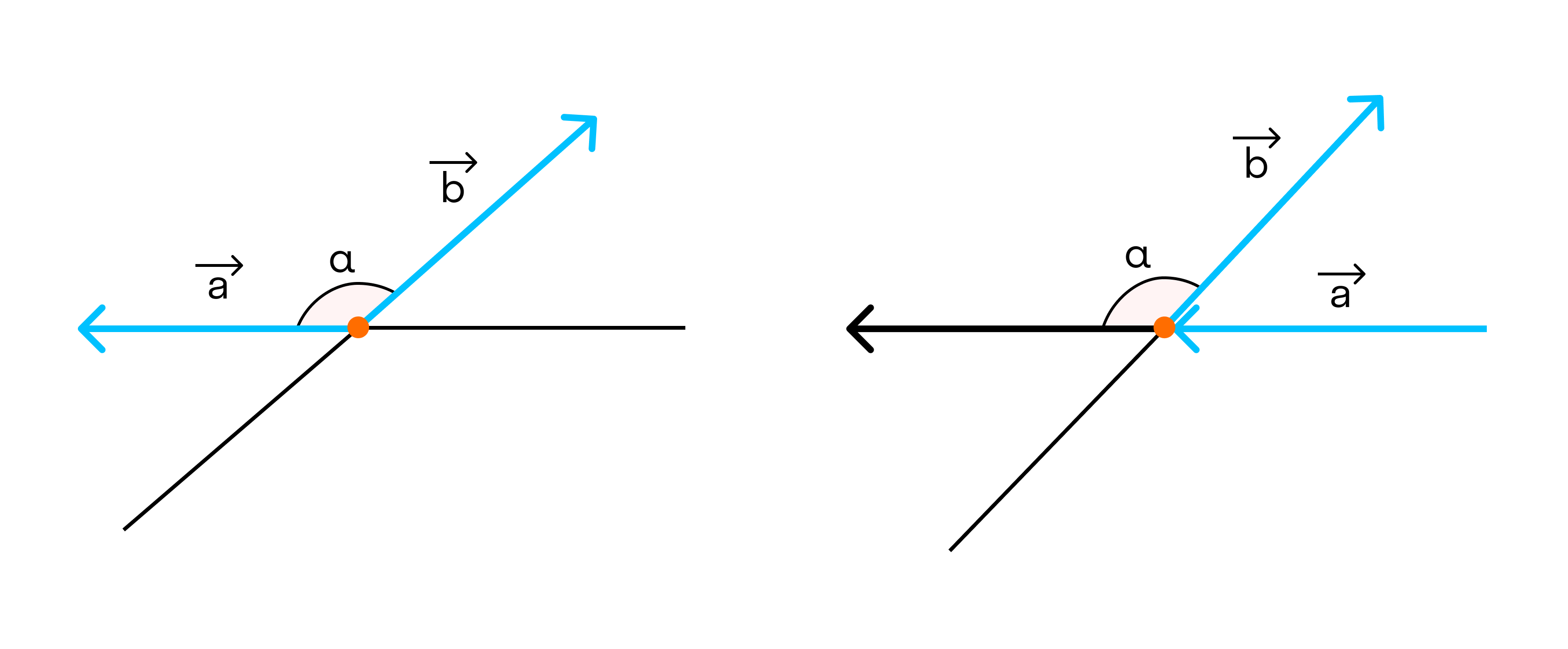
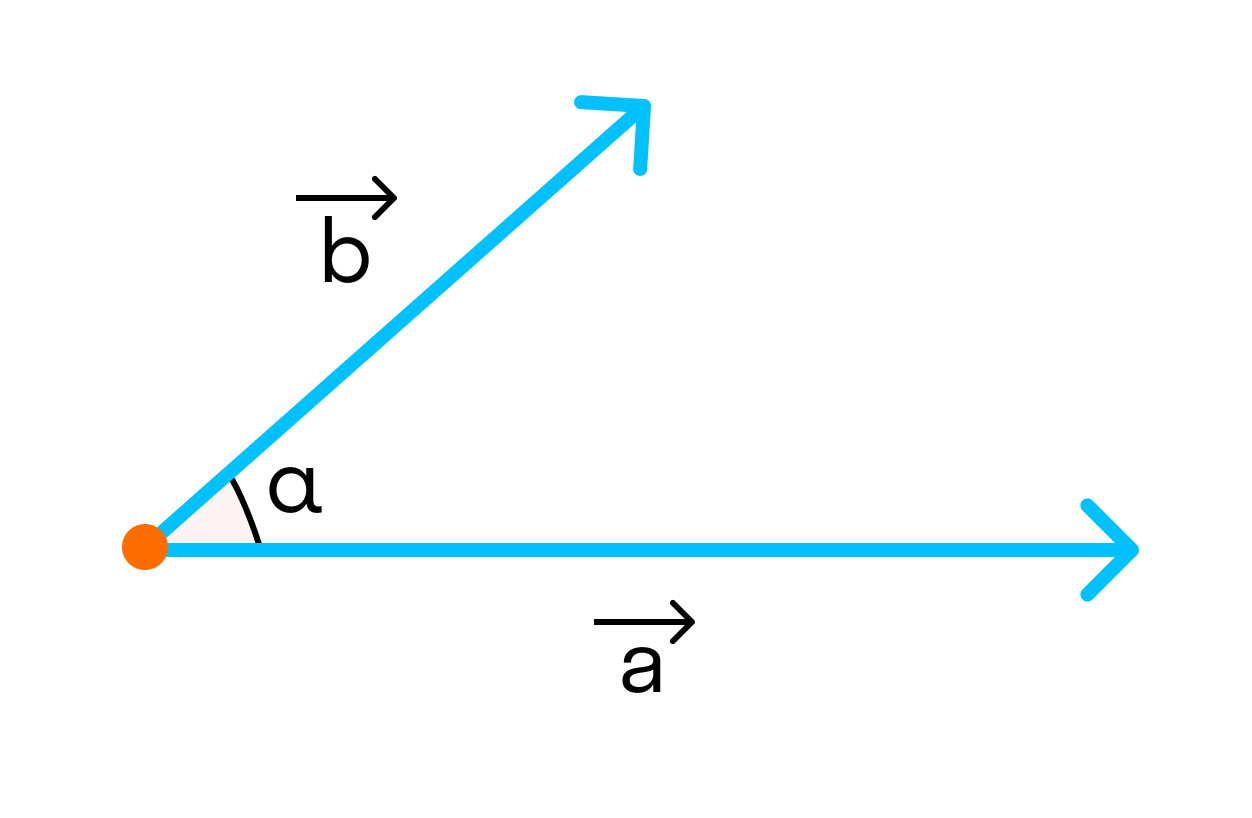
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

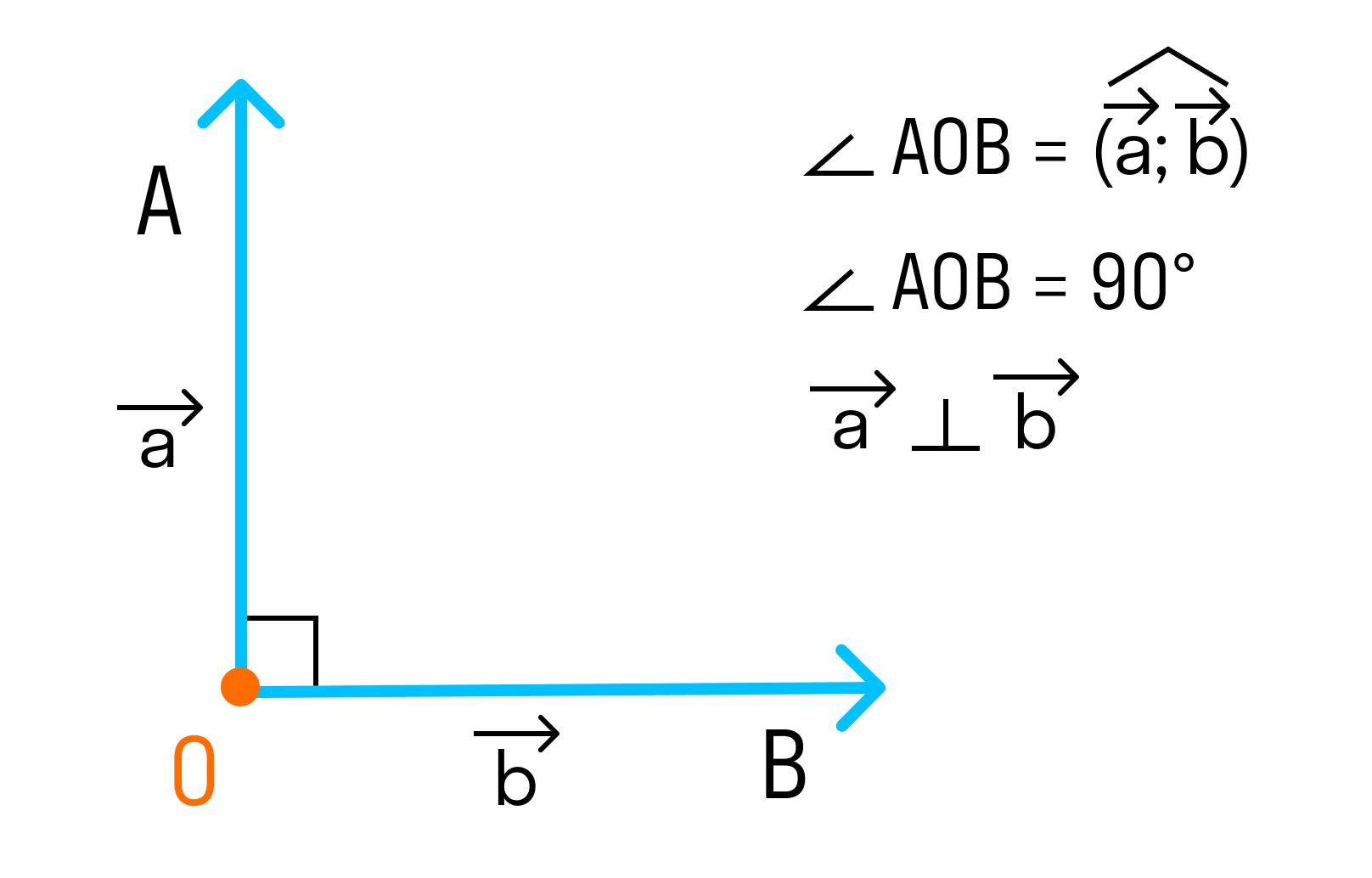
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

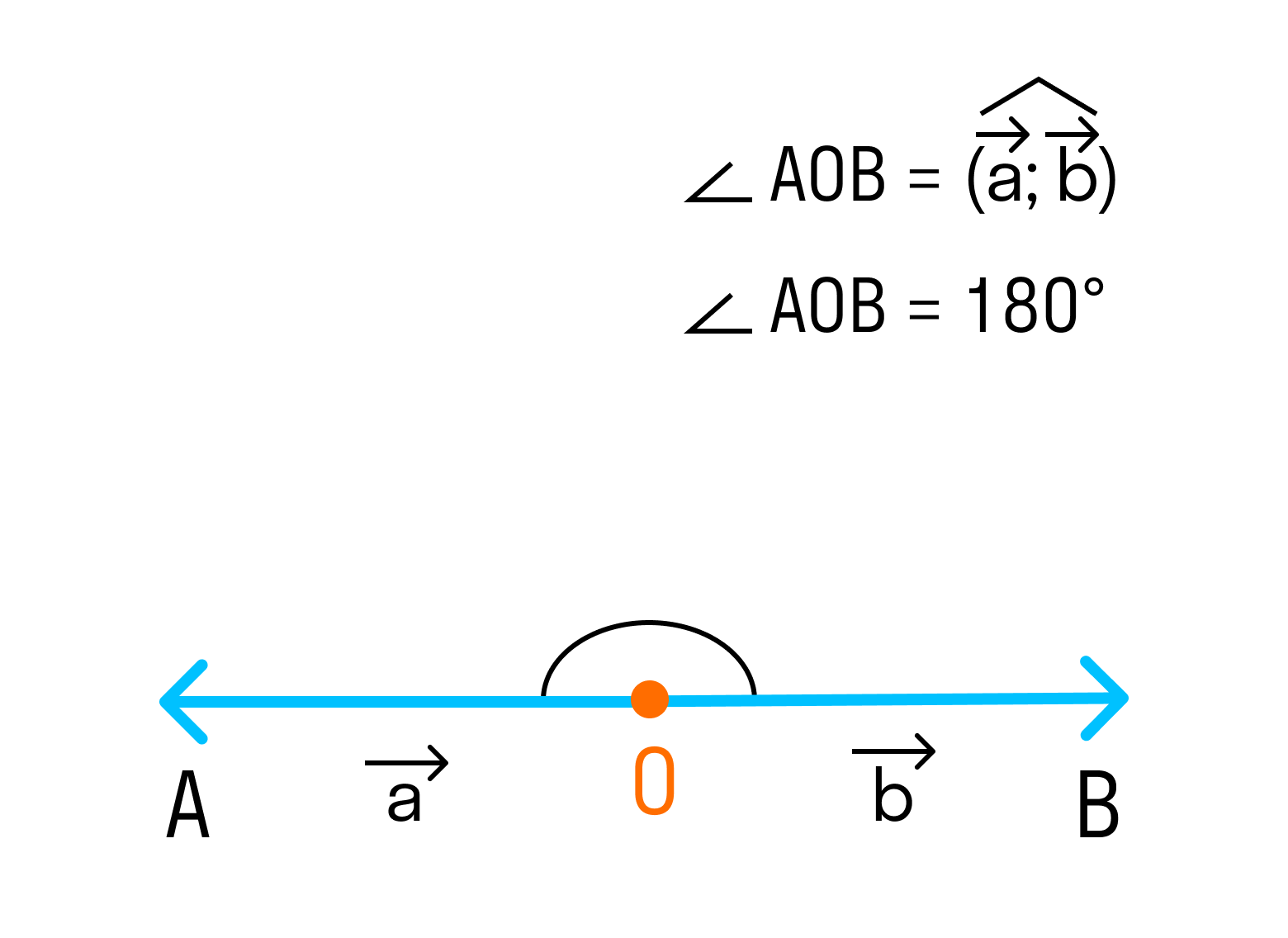
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

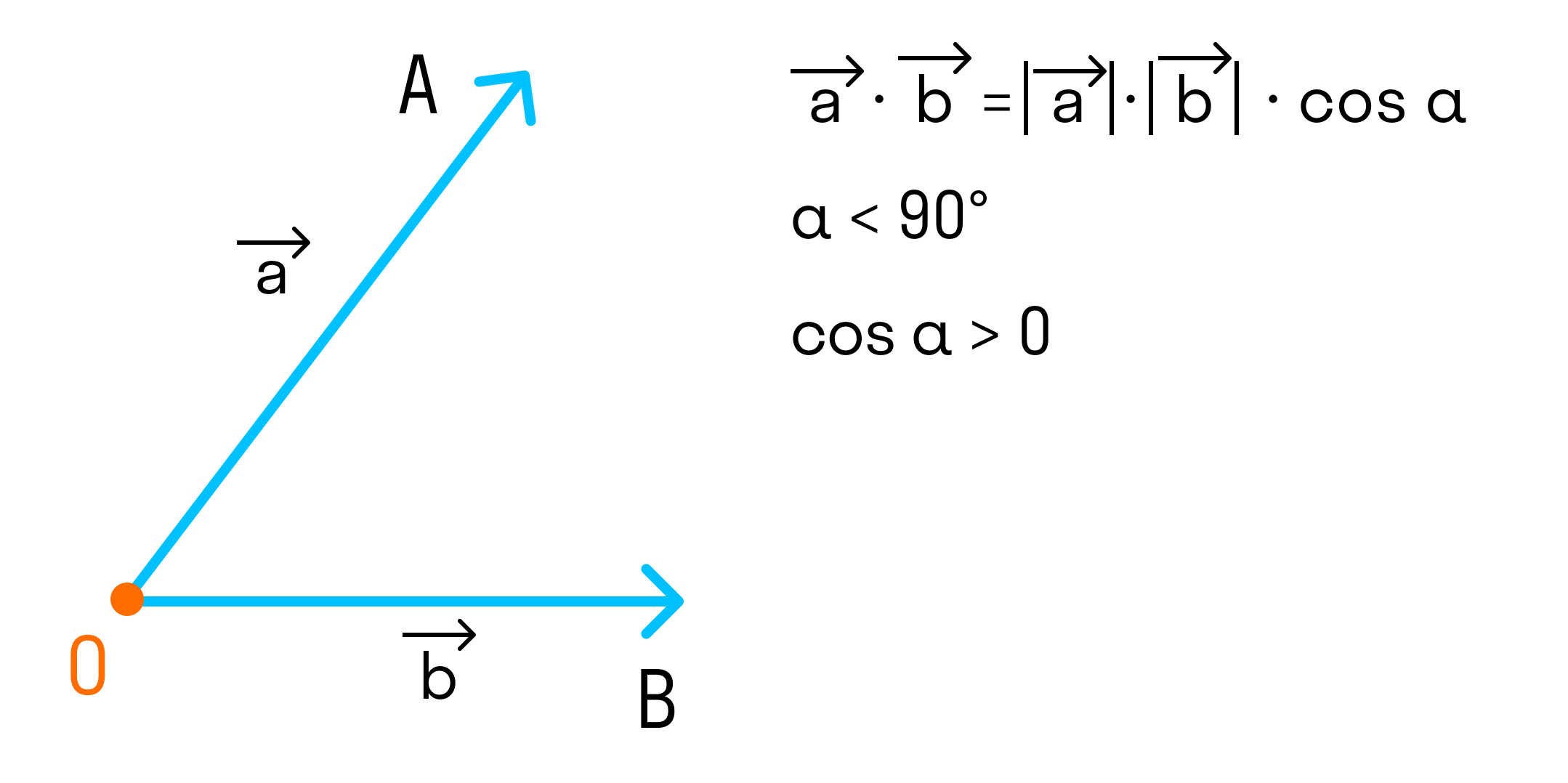
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

→a * →b = →|a| * →|b| * cosα

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
• Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα

Видео:№44. Прямые ОВ и CD параллельные, а ОА и CD — скрещивающиеся прямые.Скачать

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

Сначала докажем равенства

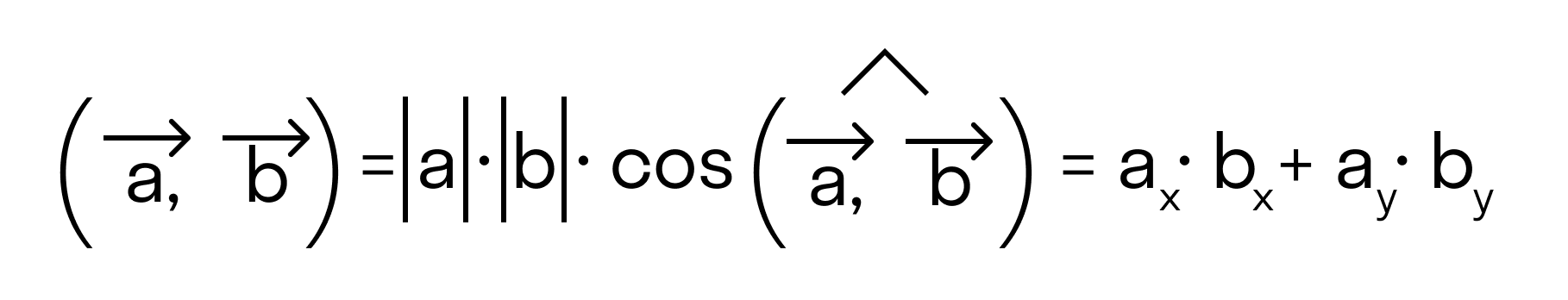
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

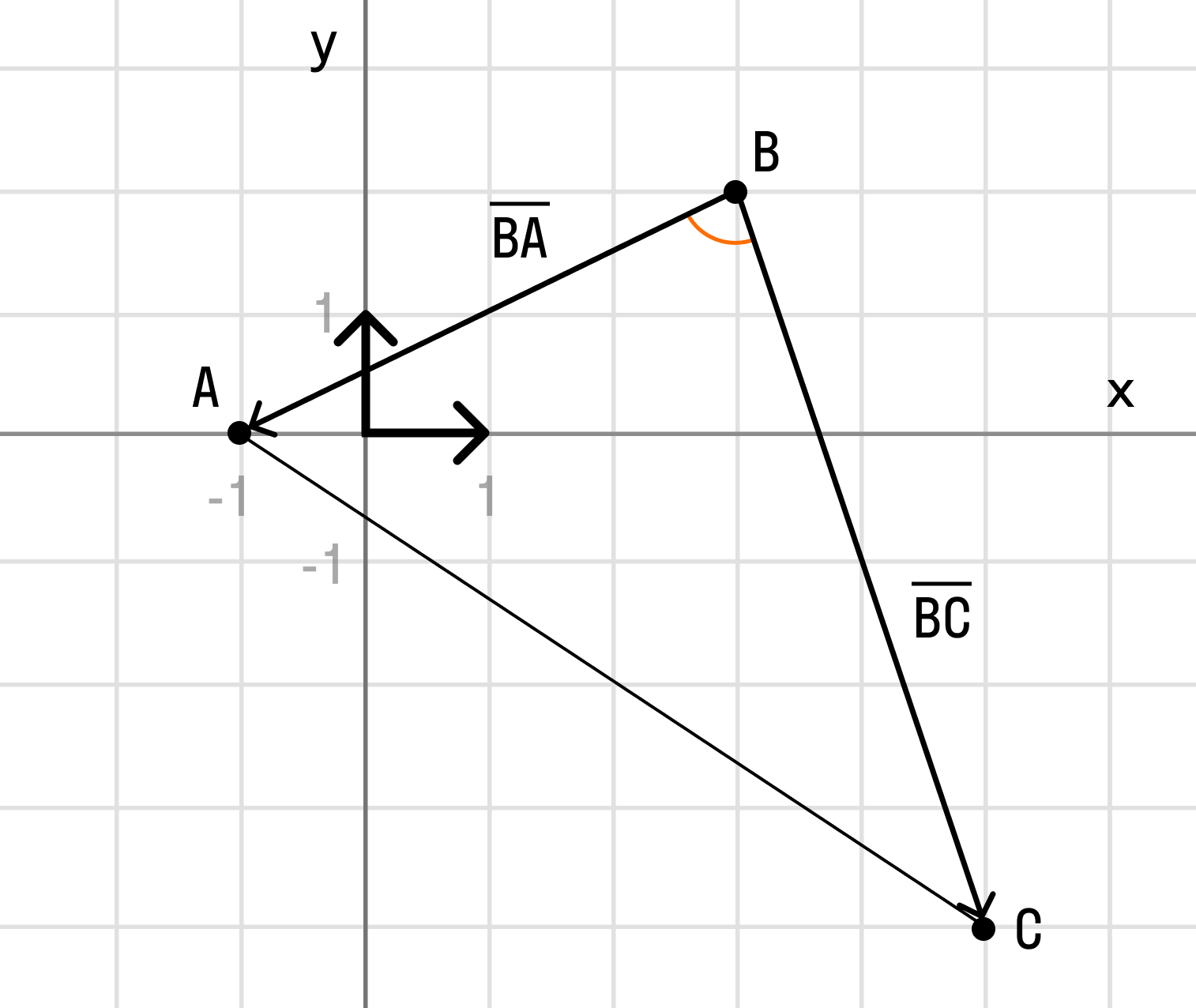
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Вспомнив формулу вычисления длины вектора по координатам, получаем

Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

В n-мерном пространстве скалярное произведение векторов a = и b = можно найти по формуле:

a * b = a1 * b1 + a2 * b2 + . + an * bn

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Свойства скалярного произведения

Свойства скалярного произведения векторов:

Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.

→0 * →0 = 0

Скалярное произведение вектора самого на себя равно квадрату его модуля:

→a * →a = →∣∣a∣∣2

Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:

→a * →b = →b * →a

Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:

(→a + →b) * →c = →a * →c + →b * →c

Сочетательный закон для скалярного произведения:

(k * →a) * →b = k * (→a * →b)

Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

В данном случае:

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Введем систему координат.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Найдем координаты векторов →AB1 и →BC1:

Найдем длины векторов →AB1 и →BC1:

Найдем скалярное произведение векторов →AB1 и →BC1:

Найдем косинус угла между прямыми AB1 и BC1:

Пример 5.

а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)

Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.

Обратите внимание на два существенных момента:

• В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
• В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.

По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Найдём сам угол:

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

Видео:Параллельность прямых. 10 класс.Скачать

Угол между прямыми

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Определение угла между прямыми

Видео:Видеоурок "Угол между прямыми"Скачать

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

то угол между ними можно найти, используя формулу:

Если знаменатель равен нулю (1 + k ₁· k ₂ = 0), то прямые перпендикулярны.

Соответственно легко найти угол между прямыми

tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k ₁ — k ₂ 1 + k ₁· k ₂

Угол между прямыми через направляющие векторы этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано параметрически

x = l t + a y = m t + b

то вектор направляющей имеет вид

Если уравнение прямой задано как

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .

Если дано каноническое уравнение прямой

то вектор направляющей имеет вид

Если задано уравнение прямой с угловым коэффициентом

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =

Угол между прямыми через векторы нормалей этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано как

то вектор нормали имеет вид

Если задано уравнение прямой с угловым коэффициентом

то вектор нормали имеет вид

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

sin φ = | a · b | | a | · | b |

Видео:14. Угол между прямыми в пространствеСкачать

Примеры задач на вычисления угла между прямыми на плоскости

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k ₁ — k ₂ 1 + k ₁· k ₂ = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор , для второй прямой направляющий вектор

cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2 x + 3 y = 0 => y = — 2 3 x ( k ₁ = — 2 3 )

x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k ₂ = 4 3 )

tg γ = k ₁ — k ₂ 1 + k ₁· k ₂ = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18

Видео:Теорема 14.3 Если соответственные углы равны, то прямые параллельны || Геометрия 7 класс ||Скачать

Угол между прямыми в пространстве

cos φ = | a · b | | a | · | b |

Если дано каноническое уравнение прямой

то направляющий вектор имеет вид

Если уравнение прямой задано параметрически

x = l t + a y = m t + b z = n t + c

то направляющий вектор имеет вид

Решение: Так как прямые заданы параметрически, то — направляющий вектор первой прямой, направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор .

Преобразуем второе уравнение к каноническому вид.

1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3

3 z — 5 2 = z — 5/3 2/3

Получено уравнение второй прямой в канонической форме

x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3

— направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205

📸 Видео

Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

10 класс, 9 урок, Угол между прямымиСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельные прямые (задачи).Скачать

Расстояние между параллельными прямымиСкачать