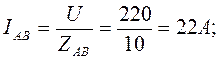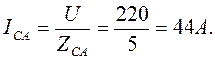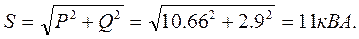Пример №1
Задача
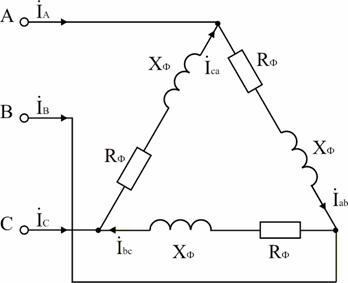
В трехфазную сеть с UЛ = 380 В включен соединенный треугольником трехфазный асинхронный двигатель мощностью P = 5 кВт, КПД двигателя равен ηН = 90%, коэффициент мощности cos φН = 0,8. Определить фазные и линейные токи двигателя, параметры его схемы замещения RФ, XФ, построить векторную диаграмму. Включить ваттметры для измерения активной мощности и найти их показания.
Анализ и решение задачи
Двигатель является активно-индуктивным потребителем энергии, его схема замещения приведена на рис. 2
Расчет активной мощности и токов, потребляемых двигателем из сети.
В паспорте двигателя указывается механическая мощность на валу; потребляемая активная мощности двигателя
P = PН / η = 500 / 0.9 = 5560 Вт.
Для симметричной нагрузки, какой является двигатель,
P = 3 UФ IФ cos φ и IФ = P / (3 UФ cos φ).
IФ = 5560 / (3 · 380 · 0,8) = 6,09 А.
IЛ = 
Расчет параметров схемы замещения двигателя.
ZФ = UФ / IФ = 380 / 6,09 = 62,4 Ом; RФ = ZФ cos φ = 62,4 · 0,8 = 49,9 Ом;
XФ = ZФ sin φФ = 62,4 · 0,6 = 37,4 Ом; cos φФ = cos φН = 0,8.
Построение векторной диаграммы.
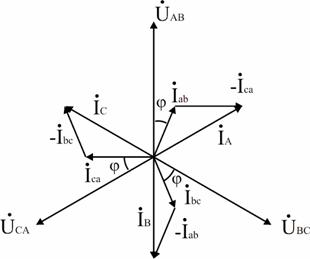
Линейные напряжения строятся в виде симметричной звезды, они же являются в данном случае фазными напряжениями. Фазные токи отстают от напряжений на угол φФ, линейные токи строятся по фазным на основании уравнений, составленных по первому закону Кирхгофа:
Векторная диаграмма показана на рис. 3
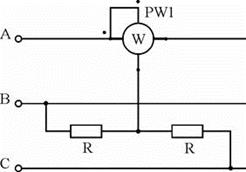
Схема включения ваттметров.
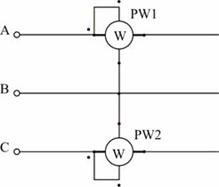
В трехпроводных сетях часто для измерения активной мощности применяется схема двух ваттметров, один из вариантов которой показан на рисунке 4. Показания ваттметра определяются произведением напряжения, приложенного к его катушке напряжения, на ток в токовой катушке и косинус угла между ними:
Активная мощность трехфазной цепи равна алгебраической сумме показаний приборов: P = P1 + P2 = 1573 + 3976 = 5549 Вт.
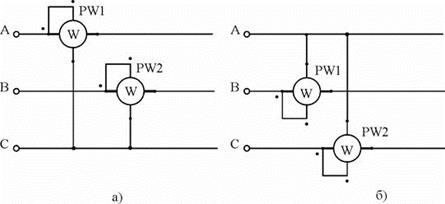
На рисунке 5 показано еще два варианта подключения приборов по схеме двух ваттметров.
При симметричной нагрузке можно измерить мощность одним ваттметром, подключив его обмотку напряжения к соответствующему фазному напряжению сети (если доступна нейтральная точка) или создав искусственную точку (рис. 6), при этом прибор измеряет мощность одной фазы, мощность всей цепи Pцепи = 3 PW.
Пример № 2
Задача
К источнику с UЛ = 220 В подключена соединенная треугольником осветительная сеть. Распределение нагрузки по фазам: PAB = 2200 Вт, PBC = 3300 Вт, PCA = 4400 Вт. Вычислить активную мощность, потребляемую схемой из сети, фазные и линейные токи приемников.
Анализ и решение задачи
Активная мощность всей нагрузки равна сумме мощностей фаз:
P = PAB + PBC + PCA = 2200 + 3300 + 4400 = 9900 Вт.
Расчет фазных токов. Т.к. осветительная сеть имеет cos φ = 1, для любой фазы IФ = PФ / UФ, поэтому:
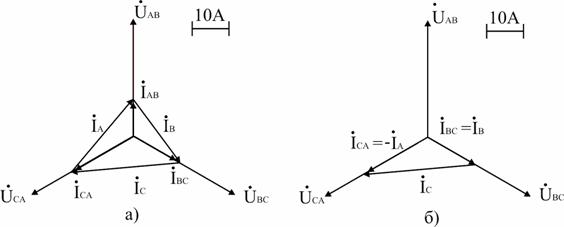
Аналитический расчет линейных токов выполняется комплексным методом на основании 1-го закона Кирхгофа; определим их графически, построив векторную диаграмму (рис. 7, а)
Из диаграммы следует: IA = 27,6 А; IB = 22,8 А; IC = 26,6 А.
Задание 1. Выполните расчет трехфазной цепи по условиям задачи 1.
В трехфазную сеть с UЛ = 380 В включен по схеме треугольник асинхронный двигатель, имеющий ZФ = 19 Ом, cos φФ = 0,8. Найти линейные токи и активную мощность, потребляемую двигателем из сети.
Ответ: 34,6 А; 18,2 кВт.
Задание 2. Выполните расчет трехфазной цепи по условиям задачи 2.
Трехфазная печь включена в сеть с UЛ = 380 В по схеме треугольник. Найти линейный ток и мощность печи, если RФ = 10 Ом. Как изменятся линейный ток и мощность печи, если ее включить в ту же сеть по схеме звезда?
Ответ: 65,7 А; 43,2 кВт; 21,9 А; 14,4 кВт.
Контрольные вопросы
1. Начертите схему соединения потребителей по способу «треугольник» и подключения их к трехфазной сети.
2. Как определить общую активную Р, реактивную Q и полную S мощности электроприемников в несимметричной трехфазной цепи при их соединении треугольником?
3. Как определить общую активную Р, реактивную Q и полную S мощности электроприемников в симметричной трехфазной цепи при их соединении треугольником?
4. Как определить активную Рф, реактивную Qф и полную Sф мощности для отдельной фазы?
5. Запишите соотношение между фазными и линейными токами при соединении «треугольником»?
6. Запишите соотношение между фазными и линейными напряжениями при соединении «треугольником»?
7. Опишите, что произойдет в системе трехфазного питания при обрыве одного из линейных проводов.
Видео:Трехфазные цепи - Задача 1. Расчет трехфазной цепи соединенной звездойСкачать
Задачи на трехфазные цепи
Трехфазные электрические цепи получили широкое распространение в промышленности, благодаря своим немалым преимуществам перед другими системами электрических цепей. К ним относятся – экономичность передачи энергии, относительная простота создания вращающегося магнитного поля, а также возможность получения двух значений напряжения. Основными потребителями трехфазных систем являются асинхронные двигатели, а основными источниками – трехфазные генераторы.
В разделе электротехники трехфазным цепям переменного тока посвящено немало задач, рассмотрим решение некоторых из них.
Видео:Трехфазные цепи - ТРЕУГОЛЬНИК. Расчет трехфазной цепи, соединенной треугольникомСкачать
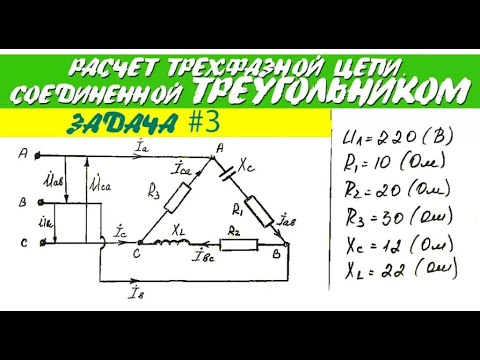
Задача 1
Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю.
а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом
Линейные напряжения в данном случае будут равны и определяться как
б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения.
Линейные напряжения в данном примере будут разными по значению
в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ.
Как и в предыдущем примере, линейные напряжения не будут равны
Видео:7. Решение задачи на трехфазные цепи по схеме треугольника.Скачать

Задача 2
К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A1,A2 и фазные токи зная, что Uл=380В, R=50 Ом, xL=35 Ом.
Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)
Напряжения в фазах будет равно
Токи в фазах
Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)
Соответственно, показания амперметров будут следующими:
К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, xL=xC=10 Ом.
Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений


Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа
Сумма линейных токов
Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.
Чтобы определить показания вольтметра, найдём сумму падений напряжения на xL и R в соответствующих обмотках.

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Задачи на трехфазные цепи с решениями
Puc. 6.
Задача: В каждую фазу трехфазной четырехпроводной сети включили сопротивления так, как показано на рис. 6. Величины сопротивлений даны на рисунке. Линейное напряжение сети U=380B. Определить: линейные токи, углы сдвига фаз, ток в нулевом проводе, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.
Решение. 1. Полные сопротивления фаз:
2. Углы сдвига фаз:



3. Фазное напряжение
4. Линейные (фазные) токи:
5. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз
6. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз
Знак «минус» показывает, что реактивная мощность системы носит емкостный характер.
7. Полная мощность трех фаз:
8. Построение векторной диаграммы начинаем с векторов фазных напряжений.
Рис. 7.
Из точки О (рис. 7) в принятом масштабе напряжений проводим три вектора фазных напряжений 




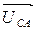










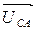




Черточки над буквами показывают, что векторы должны вычитаться и складываться геометрически. Например, для построения линейного напряжения 


Под углом φА=53° в сторону опережения вектора фазного напряжения 


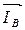
Вектор тока 

Для определения тока в_нулевом проводе I складываем геометрически векторы токов 


Пример 2:В каждую фазу трехфазной сети включили сопротивления так, как показано на рис. 8. Величины сопротивлений даны на рисунке3. Линейное напряжение сети U =220B.
Рис. 8.
Определить: фазные и линейные токи, углы сдвига фаз, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.
Решение 1. Полные сопротивления фаз:
2. Углы сдвига фаз:


4. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз
5. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз
6. Полная мощность трех фаз
7. Для определения линейных токов строим векторную диаграмму (рис. 4). Построение _начинаем с векторов фазных (линейных) напряжений 


Вектор тока 

Вектор тока 



Линейные токи 
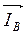




Из векторной диаграммы графически, пользуясь масштабом, определяем линейные токи: IA=66A; IB=43A; IC=25A.
Puc. 6.
Задача: В каждую фазу трехфазной четырехпроводной сети включили сопротивления так, как показано на рис. 6. Величины сопротивлений даны на рисунке. Линейное напряжение сети U=380B. Определить: линейные токи, углы сдвига фаз, ток в нулевом проводе, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.
Решение. 1. Полные сопротивления фаз:
2. Углы сдвига фаз:



3. Фазное напряжение
4. Линейные (фазные) токи:
5. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз
6. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз
Знак «минус» показывает, что реактивная мощность системы носит емкостный характер.
7. Полная мощность трех фаз:
8. Построение векторной диаграммы начинаем с векторов фазных напряжений.
Рис. 7.
Из точки О (рис. 7) в принятом масштабе напряжений проводим три вектора фазных напряжений 




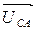










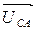




Черточки над буквами показывают, что векторы должны вычитаться и складываться геометрически. Например, для построения линейного напряжения 


Под углом φА=53° в сторону опережения вектора фазного напряжения 


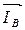
Вектор тока 

Для определения тока в_нулевом проводе I складываем геометрически векторы токов 


Пример 2:В каждую фазу трехфазной сети включили сопротивления так, как показано на рис. 8. Величины сопротивлений даны на рисунке3. Линейное напряжение сети U =220B.
Рис. 8.
Определить: фазные и линейные токи, углы сдвига фаз, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму.
Решение 1. Полные сопротивления фаз:
2. Углы сдвига фаз:


4. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз
5. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз
6. Полная мощность трех фаз
7. Для определения линейных токов строим векторную диаграмму (рис. 4). Построение _начинаем с векторов фазных (линейных) напряжений 


Вектор тока 

Вектор тока 



Линейные токи 
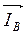




Из векторной диаграммы графически, пользуясь масштабом, определяем линейные токи: IA=66A; IB=43A; IC=25A.
Трехфазные электрические цепи получили широкое распространение в промышленности, благодаря своим немалым преимуществам перед другими системами электрических цепей. К ним относятся – экономичность передачи энергии, относительная простота создания вращающегося магнитного поля, а также возможность получения двух значений напряжения. Основными потребителями трехфазных систем являются асинхронные двигатели, а основными источниками – трехфазные генераторы.
В разделе электротехники трехфазным цепям переменного тока посвящено немало задач, рассмотрим решение некоторых из них.
Видео:Расчет Трехфазной цепи Без комплексных чисел. Соединение треугольникомСкачать

Задача 1
Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю.
а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом
Линейные напряжения в данном случае будут равны и определяться как
б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения.
Линейные напряжения в данном примере будут разными по значению
в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ.
Как и в предыдущем примере, линейные напряжения не будут равны
Видео:6. Решение задачи на трехфазные цепи Соединённые по схеме звездаСкачать

Задача 2
К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A1,A2 и фазные токи зная, что Uл=380В, R=50 Ом, xL=35 Ом.
Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)
Напряжения в фазах будет равно
Токи в фазах
Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)
Соответственно, показания амперметров будут следующими:
К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, xL=xC=10 Ом.
Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений


Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа
Сумма линейных токов
Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.
Чтобы определить показания вольтметра, найдём сумму падений напряжения на xL и R в соответствующих обмотках.

💡 Видео
Лекция 060-2. Расчет трехфазных цепейСкачать

Трехфазные электрические цепи │Теория ч. 1Скачать

Трехфазные электрические цепи. Соединение треугольникомСкачать

Расчет трехфазной цепи │ЗВЕЗДА С НУЛЕВЫМ ПРОВОДОМСкачать

Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

Соединение трехфазных цепей звездой и треугольникомСкачать

Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать

Чернышова Т Ю Теоретические основы электротехники Трехфазная цепь, соединение треугольникСкачать

Симметричная нагрузка в трехфазной цепиСкачать

Трехфазная система. Анимация электрических процессовСкачать

Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Расчет трехфазной цепиСкачать

Схема треугольник (трехфазные цепи)Скачать