Дан выпуклый четырехугольник abcd x середина диагонали ac оказалось что cd bx найдите ad если

Этап проводился дистанционно. На ввод ответов отводилось 120 минут.

читать дальше 1. Найдите наибольшее пятизначное число, произведение цифр которого равно 120.

2. В течение первого полугодия лентяй Паша заставлял себя решать задачи по математике. Каждый день он решал не более 10 задач, а если в какой-нибудь день он решал больше 7 задач, то следующие два дня он решал не более 5 задач в день. Какое наибольшее количество задач Паша мог решить за 7 подряд идущих дней?

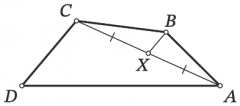
3. Дан выпуклый четырёхугольник $ABCD,$ $X$ — середина диагонали $AC.$ Оказалось, что $CDparallel BX.$ Найдите $AD,$ если известно, что $BX=3,$ $BC=7,$ $CD=6.$

4. Про положительные числа $a, b, c$ известно, что [ frac = 7,quad frac = 175. ]
Чему равняется $dfrac ?$

5. Точка $M$ — середина стороны $BC$ треугольника $ABC,$ в котором $AB=17,$ $AC=30,$ $BC=19.$ На стороне $AB$ как на диаметре построена окружность. На этой окружности выбирается произвольная точка $X.$ Какое минимальное значение может принимать длина отрезка $MX?$

6. Дана белая клетчатая таблица $8times8.$ В ней 20 клеток покрасили в чёрный цвет. Какое наименьшее количество пар соседних по стороне белых клеток могло остаться?

7. Стороны квадрата $ABCD$ параллельны осям координат, причём $AB$ лежит на оси ординат, а сам квадрат расположен так, как показано на рисунке. Парабола, задаваемая уравнением [ y = frac x^2 + ax + b,] проходит через точки $B$ и $C.$ Кроме этого, вершина этой параболы (точка $E$) лежит на отрезке $AD.$ Найдите сумму корней квадратного трёхчлена, графиком которого является парабола.

8. По кругу стоят 73 ребёнка. Злой Дед Мороз обходит круг по часовой стрелке и раздаёт конфеты. Вначале он выдал первому ребёнку одну конфету, затем 1 ребёнка пропустил, следующему ребёнку выдал одну конфету, затем 2 детей пропустил, следующему ребёнку выдал одну конфету, затем 3 детей пропустил и так далее. Раздав 2020 конфет, он ушёл. Сколько детей так и не получили конфеты?

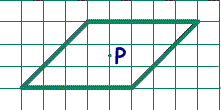
читать дальше 1. На какое наименьшее число клетчатых прямоугольников можно разрезать фигуру на рисунке? (Каждый прямоугольник должен состоять из одной или нескольких клеток фигуры.)

2. Сколько корней имеет уравнение [ overbrace^<10textf>(x). )) + frac = 0, ] где $f(x) = |x|-1?$

3. Антон выписал на доску три натуральных числа: $a,$ $b$ и $c.$ А Ира нарисовала на доске три прямоугольника: $atimes b,$ $atimes c$ и $btimes c.$ Оказалось, что разность площадей какой-то пары прямоугольников равна $1,$ а разность площадей другой пары прямоугольников равна 49. Чему может быть равно $a+b+c?$ Укажите все возможные варианты.

4. Равнобедренная трапеция $ABCD$ с основаниями $BC$ и $AD$ такова, что $angle ADC = 2angle CAD = 82^circ.$ Внутри трапеции выбрана точка $T$ так, что $CT=CD,$ $AT=TD.$ Найдите $angle TCD.$

5. Целые числа $a$ и $b$ таковы, что у квадратных трёхчленов $x^2+ax+b$ и $x^2+bx+1100$ есть общий корень, являющийся простым числом. Найдите $a.$ Укажите все возможные варианты.

6. На острове живут два племени: рыцари и лжецы. Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды 80 человек сели за круглый стол, и каждый из них заявил: «Среди 11 человек, сидящих следом за мной по часовой стрелке, есть хотя бы 9 лжецов». Сколько рыцарей сидит за круглым столом? Укажите все возможные варианты.

7. Дан прямоугольный треугольник $ABC$ с катетами $AB=42$ и $BC=56.$ Окружность, проходящая через точку $B,$ пересекает сторону $AB$ в точке $P,$ сторону $BC$ — в точке $Q,$ а сторону $AC$ — в точках $K$ и $L.$ Известно, что $PK=KQ$ и $QL:PL=3:4.$ Найдите $PQ^2.$

8. Два разбойника украли 300 золотых монет. Они решили поделить их следующим образом: первый разбойник кладёт в мешочек несколько монет (возможно, все), а второй разбойник выбирает, кому этот мешочек достанется; затем это действие повторяется ещё несколько раз. Делёж заканчивается, когда

либо все деньги кончились,
либо кому-нибудь досталось 11 мешочков, в этом случае все остальные деньги сразу же достаются другому разбойнику.

Какое наибольшее количество монет может гарантированно получить первый разбойник?

читать дальше 1. Учитель написал на доске двузначное число. Каждый из троих ребят сказал по два утверждения.

Андрей: «это число заканчивается на цифру 6» и «это число делится на 7».
Боря: «это число больше 26» и «это число заканчивается на цифру 8».
Саша: «это число делится на 13» и «это число меньше 27».

Известно, что каждый из мальчиков один раз сказал правду и один раз ошибся. Какое число могло быть написано на доске? Укажите все возможные варианты.

2. У Веры есть набор различных по массе гирь, каждая из которых весит целое число грамм. Известно, что самая лёгкая гиря набора весит в 71 раз меньше, чем все остальные гири вместе взятые. Также известно, что две самые лёгкие гири набора вместе весят в 34 раза меньше, чем все остальные гири вместе взятые. Какое наименьшее число грамм может весить самая лёгкая гиря?

3. На координатной плоскости отметили все точки $(x, y)$ такие, что $x$ и $y$ — целые числа, удовлетворяющие неравенствам $0le xle 2$ и $0le yle 26.$ Сколько существует прямых, проходящих ровно через 3 отмеченные точки?

4. На стороне $AC$ треугольника $ABC$ отмечены точки $M$ и $N$ ($M$ лежит на отрезке $AN$). Известно, что $AB=AN,$ $BC=MC.$ Описанные окружности треугольников $ABM$ и $CBN$ пересекаются в точках $B$ и $K.$ Сколько градусов составляет угол $AKC,$ если $angle ABC = 68^circ?$

5. В шахматном турнире соревнуются друг с другом команда школьников и команда студентов, в каждой из которых по 15 человек. В течение турнира каждый школьник должен сыграть с каждым студентом ровно один раз, причём каждый день каждый человек должен играть не более одного раза. В некоторый момент турнира организатор заметил, что может составить расписание на следующий день из 15 игр ровно 1 способом, а из 1 игры — $N$ способами (порядок игр в расписании не важен, важно лишь кто с кем играет). Найдите наибольшее возможное значение $N.$

6. Дан выпуклый четырёхугольник $ABCD.$ Известно, что $angle C 57^circ,$ $sin angle A + sin angle B = sqrt$ и $cos angle A + cos angle B = 2 — sqrt.$ Сколько градусов составляет угол $D?$

7. Натуральные числа $a$ и $b$ таковы, что $a^a$ делится на $b^b,$ однако $a$ не делится на $b.$ Найдите наименьшее возможное значение числа $a+b,$ если известно, что число взаимно просто с 210.

8. Внутри тетраэдра $ABCD$ даны точки $X$ и $Y.$ Расстояния от точки $X$ до граней $ABC,$ $ABD,$ $ACD,$ $BCD$ равны 14, 11, 29, 8 соответственно. А расстояния от $Y$ точки до граней $ABC,$ $ABD,$ $ACD,$ $BCD$ равны 15, 13, 25, 11 соответственно. Найдите радиус вписанной сферы тетраэдра $ABCD.$

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Олимпиадные задания по математике 8 — 11 класс

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Олимпиадные задания по математике 8 — 11 класс

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Олимпиадные задания по математике 8 класс

1. На доске была нарисована система координат и отмечены точки A(1;2) и B(3;1). Систему координат стерли. Восстановите ее по двум отмеченным точкам.

2. В некотором треугольнике биссектрисы двух внутренних углов продолжили до пересечения с описанной окружностью и получили две равные хорды. Верно ли, что треугольник равнобедренный?

3. В правильном шестиугольнике АВСDEF на прямой AF взята точка X так, что угол XСD = 45 o . Найдите угол FXE.

4. Около четырехугольника ABCD можно описать окружность. Точка p – основание перпендикуляра, опущенного из точки А на прямую ВС, Q – из А на DC, R – из D на АВ и Т – из D на ВС. Докажите, что точки p, Q, R и T лежат на одной окружности.

5. Восстановите остроугольный треугольник по ортоцентру и серединам двух сторон.

6. Противоположные стороны выпуклого шестиугольника ABCDEF параллельны. Назовем его «высотами» векторы с концами на прямых, содержащих противолежащие стороны, перпендикулярные им и направленные от AB к DE, от EF к BC и от CD к AF. Докажите, что вокруг этого шестиугольника можно описать окружность тогда и только тогда, когда сумма его «высот» равна нулевому вектору.

Видео:#58. Олимпиадная задача о четырехугольникеСкачать

Олимпиадные задания по математике 8 класс

1. Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника.

2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК .

3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей.

4. В трапеции ABCD : AB = BC = CD , CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС , проходит через середину BD .

5. Пусть AA ₁ и BB ₁ – высоты неравнобедренного остроугольного треугольника АВС , М – середина АВ . Окружности, описанные около треугольников AMA ₁ и BMB ₁ пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К , М и L лежат на одной прямой.

6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Олимпиадные задания по математике 9 класс

1. Постройте треугольник по стороне, противолежащему углу и медиане, проведенной к другой стороне ( исследование вопроса о количестве решений не требуется ).

2. В выпуклом четырехугольнике ABCD Ð ABC = 90 0 , Ð BAC = Ð CAD , AC = AD , DH — высота треугольника ACD . В каком отношении прямая BH делит отрезок CD ?

3. Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС . На окружностях (в одной полуплоскости относительно АС ) выбраны соответственно точки M и L так, что Ð MBA = Ð LBC . Точки K и F отмечены соответственно на лучах ВМ и BL так, что BK = BC и BF = AB . Докажите, что точки M , K , F и L лежат на одной окружности.

4. В треугольнике ABC M — точка пересечения медиан, O — центр вписанной окружности, A’ , B’ , C’ — точки ее касания со сторонами BC , CA , AB соответственно. Докажите, что, если CA’ = AB , то прямые OM и AB перпендикулярны.

5. Дан треугольник АВС . Точка О 1 — центр прямоугольника ВСDE , построенного так, что сторона DE прямоугольника содержит вершину А треугольника. Точки О 2 и О 3 являются центрами прямоугольников, построенных аналогичным образом на сторонах АС и АВ соответственно. Докажите, что прямые АО 1 , ВО 2 и СО 3 пересекаются в одной точке.

6. На плоскости расположен круг. Какое наименьшее количество прямых надо провести, чтобы, симметрично отражая данный круг относительно этих прямых (в любом порядке конечное количество раз), можно было накрыть им любую заданную точку плоскости?

Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Олимпиадные задания по математике 9 класс

9.1. В выпуклом четырехугольнике АВС D Е – середина CD , F – середина А D , K – точка пересечения АС и ВЕ . Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС .

9.2. Постройте треугольник АВС по углу А и медианам, проведенным из вершин В и С .

9.3. Дан квадрат ABCD . Найдите геометрическое место точек M таких, что Ð AMB = Ð CMD .

9.4. Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке p . Точки X и Y – ортогональные проекции точки p на прямые AC и BC . Докажите, что прямая XY перпендикулярна медиане треугольника ABC , проведенной из вершины C .

9.5. Диагонали вписанного четырёхугольника ABCD пересекаются в точке M , Ð AMB = 60 ° . На сторонах AD и BC во внешнюю сторону построены равносторонние треугольники ADK и BCL . Прямая KL пересекает описанную около ABCD окружность в точках p и Q . Докажите, что pK = LQ .

9.6. Длина каждой стороны и каждой не главной диагонали выпуклого шестиугольника не превосходит 1. Докажите, что в этом шестиугольнике найдется главная диагональ, длина которой не превосходит 2 деленное на корень из 3 .

Видео:#8warmup. Разбор восьмой разминкиСкачать

Олимпиадные задания по математике 9 класс

1. На рисунке изображен параллелограмм и отмечена точка p пересечения его диагоналей. Проведите через p прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.

2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата.

4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)

5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой?

6. Фиксированы две окружности w₁ и w₂, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w₁ и w2 соответственно, а треугольник XYZ содержит окружности w₁ и w₂. Докажите, что центры окружностей, вписанных в треугольники XYZ , лежат на одной прямой.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Олимпиадные задания по математике 10 класс

10.1. Е и F – середины сторон ВС и AD выпуклого четырехугольника АВС D . Докажите, что отрезок EF делит диагонали АС и BD в одном и том же отношении.

10.2. Существует ли в пространстве замкнутая самопересекающаяся ломаная, которая пересекает каждое свое звено ровно один раз, причем в его середине?

10.3. На доске была нарисована окружность с отмеченным центром, вписанный в нее четырехугольник, и окружность, вписанная в него, также с отмеченным центром. Затем стерли четырехугольник (сохранив одну вершину) и вписанную окружность (сохранив ее центр). Восстановите какую-нибудь из стертых вершин четырехугольника, пользуясь только линейкой и проведя не более шести линий.

10.4. В треугольнике АВС : М – точка пересечения медиан, О – центр вписанной окружности. Докажите, что если прямая ОМ параллельна стороне ВС , то точка О равноудалена от сторон АВ и АС .

10.5. Трапеция АВС D с основаниями AB и CD вписана в окружность. Докажите, что четырехугольник, образованный ортогональными проекциями любой точки этой окружности на прямые AC , BC , AD и BD , является вписанным.

10.6. В тетраэдре DABC : Ð ACB = Ð ADB , ( С D ) ^ ( АВС ). В треугольнике АВС дана высота h , проведенная к стороне АВ , и расстояние d от центра описанной окружности до этой стороны. Найдите длину CD .

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Олимпиадные задания по математике 10 класс

1. Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Верно ли, что оставшиеся части также подобны?

2. Даны радиусы r и R двух непересекающихся окружностей. Общие внутренние касательные этих окружностей перпендикулярны. Найдите площадь треугольника, ограниченного этими касательными, а также общей внешней касательной.

3. Дан четырехугольник ABCD. A’, B’, C’ и D’ – середины сторон BC, CD, DA и AB соответственно. Известно, что AA’ = CC’ и BB’ = DD’. Верно ли, что ABCD параллелограмм?

4. В треугольнике АВС угол А равен 120 o . Докажите, что расстояние от центра описанной окружности до ортоцентра равно АВ + АС.

6. Есть два платка: один в форме квадрата, другой – в форме правильного треугольника, причем их периметры одинаковы. Существует ли многогранник, который можно полностью оклеить этими двумя платками без наложений (платки можно сгибать, но нельзя резать)?

6. Дан треугольник ABC и точки p и Q. Известно, что треугольники, образованные проекциями p и Q на стороны ABC, подобны (соответствуют друг другу вершины, лежащие на одних и тех же сторонах исходного треугольника). Докажите, что прямая pQ проходит через центр описанной окружности треугольника ABC.

Видео:16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать

Олимпиадные задания по математике 11 класс

1. AD и BE – высоты треугольника АВС . Оказалось, что точка C’ , симметричная вершине С относительно середины отрезка DE , лежит на стороне AB . Докажите, что АВ – касательная к окружности, описанной около треугольника DEC’ .

2. Прямая а пересекает плоскость α . Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α ?

3. Дана неравнобокая трапеция ABCD ( AB || CD ). Произвольная окружность, проходящая через точки А и В , пересекает боковые стороны трапеции в точках p и Q , а диагонали – в точках M и N . Докажите, что прямые pQ , MN и CD пересекаются в одной точке.

4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.

5. В выпуклом четырехугольнике ABCD : AC ⊥ BD , ∠ BCA = 10°, ∠ BDA = 20°, ∠ BAC = 40°. Найдите ∠ BDC . ( Ответ выразите в градусах. )

6. Пусть AA ₁, BB ₁ и CC ₁ – высоты неравнобедренного остроугольного треугольника АВС ; окружности, описанные около треугольников АВС и A ₁ B ₁ C , вторично пересекаются в точке Р , Z – точка пересечения касательных к описанной окружности треугольника АВС , проведённых в точках А и В . Докажите, что прямые АР , ВС и ZC ₁ пересекаются в одной точке.

Видео:В параллелограмме ABCD диагональ AC в 2 раза ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Олимпиадные задания по математике 11 класс

1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше?

2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь зеленой части равна сумме площадей синих частей.

3. В остроугольном треугольнике АВС проведены высоты АА₁ и ВВ₁. Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А₁СВ₁.

4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C₁ — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM₁ и BM₂. Точки A₁ и B₁ определяются аналогично. Докажите, что прямые АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник.

6. К двум окружностям w₁ и w₂, пересекающимся в точках А и В, проведена их общая касательная CD (C и D — точки касания соответственно, точка B ближе к прямой CD, чем А). Прямая, проходящая через А, вторично пересекает w₁ и w₂ в точках К и L соответственно (A лежит между K и L). Прямые KC и LD пересекаются в точке p. Докажите, что РВ — симедиана треугольника KpL (прямая, симметричная медиане относительно биссектрисы).

Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами:

Видео:Задача №255 [НЕДЕТСКАЯ ГЕОМЕТРИЯ #1]Скачать

Дан выпуклый четырехугольник abcd x середина диагонали ac оказалось что cd bx найдите ad если

Видео:ЕГЭ Математика Задание 6#27778Скачать

Источник задания: Решение 3351. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.

Задание 16. Дан выпуклый четырёхугольник ABCD со сторонами АВ = 3, ВС = CD = 5, AD = 8 и диагональю АС = 7.

а) Докажите, что около него можно описать окружность.

б) Найдите диагональ BD.

а) У любого четырехугольника вписанного в окружность, сумма противоположных углов равна 180 градусов. Покажем, что для заданного четырехугольника выполняется это свойство. Рассмотрим треугольник ABC, в котором косинус угла B в соответствии с теоремой косинусов будет равен:

Аналогично для противоположного угла D из треугольника ACD, имеем:

Таким образом, получаем, что сумма углов , следовательно, вокруг четырехугольника ABCD можно описать окружность.

б) Рассмотрим треугольник ABD и по теореме косинусов можно записать:

Также диагональ BD можно вычислить по теореме косинусов из треугольника BCD:

Вычтем (1) и (2), получим:

Подставим это значение в (1), найдем BD:

.

Ответ: .

🔥 Видео

Математика | Разбор заданий Муниципального этапа ВсОШ | 9 класс | МЭ 2020/2021Скачать

№772. Дан параллелограмм ABCD. Докажите, что ХА+ХС=XB+XD, где X— произвольнаяСкачать

Персидская олимпиадная задача по математикеСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, AB = 7. Найдите DO.Скачать

ОГЭ 2021 Ященко 8 вариант ФИПИ школе полный разбор!Скачать

ЧЕТЫРЕХУГОЛЬНИК 8 класс РЕШЕНИЕ ЗАДАЧ АтанасянСкачать