В четырехугольнике авсд стороны ав вс и сд равны по длине угол авс равен 60

Проведем диагональ АС так АВ=ВС следовательно АВС равнобедренный треугольник уголуголСАВ=уголВСА =уголВСА
уголА+уголВ+уголС=180 градусов
(180-60)/2=60
AD=CD следовательно АСD равнобедренный треугольник уголАСD=уголСАD
(180-110)/2=35
уголСАВ + уголСАD=60+35=95 угол А

Проведите BD. Известные углы разделятся пополам. 30 и 55.угол А неизвестен. В сумме эти углы должны дать 180 градусов. (30+55+угол А=180*)

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

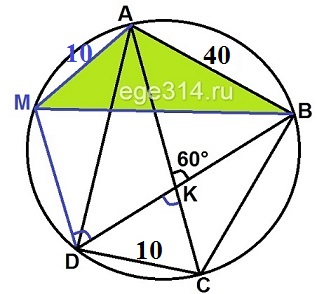
Решение №2427 Четырёхугольник ABCD со сторонами АВ = 40 и CD = 10 вписан в окружность.

Четырёхугольник ABCD со сторонами АВ = 40 и CD = 10 вписан в окружность. Диагонали АС и BD пересекаются в точке K, причём ∠AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Источник: ОГЭ Ященко 2022 (36 вар)

Проведём прямую DM параллельную АС. Дуги ‿АМ = ‿DC, значит и хорды равны DC = AM = 10.
∠ABK = ∠DKC = 60°, как вертикальные. ∠MDK = ∠DKC = 60°, как накрест лежащие углы, при AC||MD и секущей DK.
Четырёхугольник AMDB вписан в окружность, сумма противоположных углов равна 180°. Найдём ∠MAB:

∠MAB = 180° – ∠MDB = 180° – 60° = 120°

По теореме косинусов найдём MB:

MB 2 = AM 2 + AB 2 – 2·AM·AB·cos 120°

Найдём радиус описанной вокруг ΔABM окружности по теореме синусов:

Ответ: .

Видео:Задание 24 из Варианта Ларина №229 обычная версия ОГЭ-2020.Скачать

В четырехугольнике авсд стороны ав вс и сд равны по длине угол авс равен 60

В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.

а) Докажите, что вокруг этого четырёхугольника можно описать окружность.

Найдём косинусы углов ABC и ADC в треугольниках ABC и ADC соответственно:

поэтому ABC = 120°.

Далее,

поэтому ADC = 60°.

Тем самым сумма противоположных углов четырехугольника равна 180°, поэтому вокруг него можно описать окружность. Для вписанного четырёхугольника справедлива теорема Птолемея: произведение диагоналей четырёхугольника равно сумме произведений его противоположных сторон. Тогда то есть откуда

Ответ: б)

Приведем решение пункта б) Тофига Алиева без использования теоремы Птолемея.

Заметим, что поскольку Пусть тогда в треугольнике BAD по теореме косинусов

В треугольнике BCD по теореме косинусов

Приравнивая выражения для BD 2 , получим

Приведем идею решения Юрия Зорина.

Углы BAC и BDC равны как вписанные углы, опирающиеся на дугу BC. По теореме косинусов найдём косинус угла BAC (он равен 11/14). Далее, зная, что косинусы равных углов равны, из треугольника BDC найдем по теореме косинусов искомый отрезок BD.

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, 🎬 Видео №47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать 🔴 В трапеции ABCD известно, что AB=CD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону.Скачать Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать 🔴 В выпуклом четырёхугольнике ABCD известно ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать Геометрия В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8Скачать Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать Геометрия Выпуклый четырехугольник ABCD таков, что угол BAC = углу BDA и угол BAD = углу ADC = 60Скачать №369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать Четырехугольники, вписанные в окружность. 9 класс.Скачать Задание 3 ЕГЭ по математике. Урок 41Скачать ОГЭ Задание 24 Геометрическая задача на вычисление ТрапецияСкачать Решение задачи 25 из ОГЭ по математике 9 классСкачать 8 класс, 4 урок, ПараллелограммСкачать В трапеции ABCD AB=CD, ∠BDA=35° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать Угол между векторами. 9 класс.Скачать Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать Поделиться или сохранить к себе: Смотрите также Является ли четырехугольник прямоугольником если все его углы равны все его стороны равны Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 градусам Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 degree180 Является ли четырехугольник параллелограммом если его противоположные углы равны да или нет Чья комната походила как будто на сарай имела неправильный вид четырехугольника Что можно сказать о четырехугольнике если серединные перпендикуляры пересекаются в одной точке Четырехугольники авсд и дсеф имеют общую сторону сд точки а д ф Четырехугольник является правильным если все его стороны равны и один из углов