Самостоятельная работа параллельные прямые 10 класс

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Контрольные и самостоятельные работы по геометрии 10 класс (1 четверть)
учебно-методический материал по геометрии (10 класс) на тему

Контрольные и самостоятельные работы по геометрии 10 класс (1 четверть)

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Скачать:

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Предварительный просмотр:

Самостоятельная работа по геометрии № 1. Аксиомы и их следствия.

1. Сформулировать аксиомы стереометрии. Проиллюстрировать каждую аксиому.

2. Сформулировать теоремы, которые являются следствием из аксиом. Доказать любую из них.

3. Назовите 4 способа задания плоскости и выполните чертеж к каждому способу.

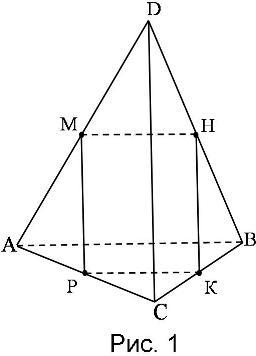
4. Пользуясь рисунком, назовите:

а) две точки, не принадлежащие плоскости (АВС)

б) прямую, по которой пересекаются плоскости (BCD) и (ABM)

в) плоскость, проходящую через прямые AM и CD

5*. Даны две прямые, через которые нельзя провести плоскость.

Могут ли эти прямые пересекаться? Ответ обоснуйте.

6*. Точка D является общей для двух различных плоскостей и и прямой а . Как может располагаться прямая а относительно и ? Укажите все возможные случаи.

1. Сформулировать аксиомы стереометрии. Проиллюстрировать каждую аксиому.

2. Сформулировать теоремы, которые являются следствием из аксиом. Доказать любую из них.

3. Назовите 4 способа задания плоскости и выполните чертеж к каждому способу.

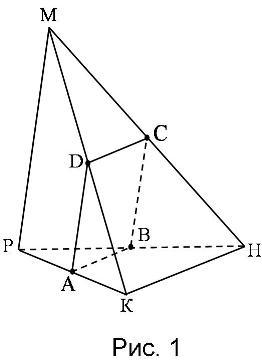
4. Пользуясь рисунком, назовите:

а) две точки, не принадлежащие плоскости (АВD)

б) прямую, по которой пересекаются плоскости (ABC) и (ADK)

в) плоскость, проходящую через прямые DK и CB

5*. Даны две плоскости, которые не пересекаются.

Могут ли эти плоскости иметь общую точку? Ответ обоснуйте.

6*. Точка D является общей для двух различных прямых a и b и плоскости . Как может располагаться прямые а и b относительно плоскости ? Укажите все возможные случаи.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Предварительный просмотр:

Самостоятельная работа по геометрии 10 класс. Тема: Параллельные прямые в пространстве.

1. Точки A, B, C, D не лежат в одной плоскости. Тогда прямые AB и CD….

1) пересекающиеся 2) параллельные 3) скрещивающиеся

2. Две прямые параллельны, если они…..

1) не пересекаются 2) перпендикулярны некоторой прямой

3) не пересекаются и лежат в одной плоскости

3) Через три точки можно провести единственную плоскость если они….

1) лежат на одной прямой 2) не лежат на одной прямой 3) совпадают

4. Прямая а параллельна плоскости . Тогда неверно, что …

1) прямая а параллельна любой прямой, лежащей в плоскости .

2) прямая а не пересекает ни одну прямую, лежащую в плоскости .

3) существует прямая, лежащая в плоскости , параллельная прямой а.

5. Какое утверждение верное?

1) если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость

2) если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая параллельна данной плоскости

3) если две прямые параллельны данной плоскости, то они параллельны друг другу.

6. Какое утверждение неверно?

1) две прямые называются параллельными, если они не имеют общих точек

2) две прямые, параллельные третьей прямой, параллельны

3) две прямые, перпендикулярные третьей прямой, параллельны.

7. Какое утверждение верное?

1) если плоскость проходит через прямую параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой

2) если прямая параллельна двум пересекающимся плоскостям, то она параллельна и линии их пересечения

3) прямые параллельные одной плоскости, параллельны

8.Точки М и N соответственно середины сторон AB и BC треугольника АВС. Прямая MN лежит в плоскости . Точка В не принадлежит данной плоскости. Тогда прямая АС …

1) лежит в плоскости 2) пересекает плоскость 3) параллельна плоскости .

9. Точка М не лежит на прямой а . Тогда неверно, что через точку М можно провести…

1) только одну прямую, не пересекающую прямую а

2) только одну прямую, параллельную прямой а

3) бесконечно много прямых, не пересекающих прямую а.

10. Дан треугольник MKP. Плоскость параллельная прямой МК пересекает МР в точке М1,

РК – в точке К1. МК = 18 см, МР : М1Р =12 : 5. Тогда длина отрезка М1К1 равна…

Самостоятельная работа по геометрии 10 класс. Тема: Параллельные прямые в пространстве.

1. Прямые AB и BC …..

1) параллельные 2) пересекающиеся 3) скрещивающиеся

2. нельзя провести плоскость через две прямые, если они….

1) параллельные 2) пересекающиеся 3) скрещивающиеся

3) Прямая лежит в плоскости некоторого треугольника, если она…

1)пересекает две стороны треугольника 2)проходит через одну из вершин треугольника

3)содержит одну из сторон треугольника.

4. Какое утверждение верно?

1) две прямые называются параллельными, если они не имеют общих точек

2) две прямые, параллельные третьей прямой, параллельны

3) две прямые, перпендикулярные третьей прямой, параллельны.

5. Прямая а параллельна плоскости . Тогда верно, что …

1) прямая а параллельна любой прямой, лежащей в плоскости .

2) прямая а не пересекает ни одну прямую, лежащую в плоскости .

3) существует прямая, лежащая в плоскости , параллельная прямой а.

6. Какое утверждение неверное?

1) если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость

2) если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая параллельна данной плоскости

3) если две прямые параллельны данной плоскости, то они параллельны друг другу

7. Какое утверждение неверное?

1) если плоскость проходит через прямую параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельны данной прямой

2) если прямая параллельна двум пересекающимся плоскостям, то она параллельна и линии их пересечения

3) прямые параллельные одной плоскости, параллельны

8. Средняя линия MN трапеции АВСD с основаниями BC и AD лежит в плоскости . Вершина А не принадлежит данной плоскости. Тогда прямая ВС…

1) лежит в плоскости 2) пересекает плоскость 3) параллельна плоскости .

9. Какое утверждение неверное?

1) если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости

2) если прямая параллельна плоскости, то она параллельна любой прямой лежащей в этой плоскости

3) если прямая параллельна плоскости, то она не пресекает ни одну прямую, лежащую в этой плоскости.

10. Дан треугольник ВСЕ. Плоскость, параллельная СЕ, пересекает ВЕ в точке Е1, ВС – в точке С1. ВС = 28 см, С1Е1 : СЕ = 3 : 8. Тогда длина отрезка ВС1 равна….

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Предварительный просмотр:

Контрольная работа по геометрии № 1. 10 класс

Тема: Аксиомы стереометрии, взаимное расположение прямых и плоскости.

1. Точка Р лежит на прямой МN . Назовите плоскость, которой принадлежит точка Р .

2. Каким плоскостям принадлежит точка К ?

3. Выберите верные высказывания:

1) Любые три точки лежат в одной плоскости.

2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости.

3) Через три точки, лежащих на прямой, проходит только одна плоскость.

4) Через две пересекающихся прямые проходит плоскость , и притом только одна

4. Выберите неверные высказывания:

1) Если три прямые имеют общую точку, то они лежат в одной плоскости.

2) Прямая, пересекающая две стороны треугольника, лежит в плоскости этого треугольника.

3) Две плоскости могут имеет только две общие точки.

4) Три попарно пересекающиеся в разных точках прямые, лежат в одной плоскости .

5. Назовите прямую, по которой пересекаются плоскости (A 1 BC) и (A 1 AD).

3) D 1 D 4) D 1 C

6. а) Прямые a и b пересекаются. Прямая с скрещивающаяся с прямой а. Могут ли прямые b и c быть параллельными? Ответ обоснуйте.

б) Прямая а параллельна плоскости α , а прямая b лежит в плоскости α . Определите, могут ли прямые а и b быть: а) параллельными б) пересекаться в) быть скрещивающимися

7. Плоскость α проходит через середины боковых сторон АВ и CD трапеции ABCD – точки M и N соответственно.

а) докажите, что AD // α ; б) Найдите ВС , если AD = 10 см, M N = 8 см.

8. Прямая МА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.

а) Докажите, что МА и ВС – скрещивающиеся прямые.

б) Найдите угол между прямыми МА и ВС , если угол MAD равен 45 градусов.

9. Две прямые параллельны, если они…..

1) не пересекаются 2) перпендикулярны некоторой прямой

3) не пересекаются и лежат в одной плоскости

10. Какое утверждение неверно?

1) две прямые называются параллельными, если они не имеют общих точек

2) две прямые, параллельные третьей прямой, параллельны

3) две прямые, перпендикулярные третьей прямой, параллельны.

11. а) Какое утверждение о прямых верное?

2)

3)

б) укажите прямые скрещивающиеся с прямой АС.

Контрольная работа по геометрии № 1. 10 класс

Тема: Аксиомы стереометрии, взаимное расположение прямых и плоскости.

1. Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

2. Каким плоскостям принадлежит точка F?

3. Выберите верные высказывания:

1) Любые четыре точки лежат в одной плоскости.

2) Через прямую и не лежащую на ней точку проходит только одна плоскость.

3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости .

4) Две плоскости могут иметь только одну общую точку.

4. Выберите неверные высказывания:

1) Две окружности, имеющие общий центр, лежат в одной плоскости .

2) Прямая, проходящая через вершину треугольника, лежит в плоскости этого треугольника.

3) Три вершины треугольника принадлежат одной плоскости.

4) Через две параллельные прямые проходит плоскость, и притом только одна.

5. Назовите прямую, по которой пересекаются плоскости DCC 1 и A 1 BC.

3) D 1 D 4) D 1 C

6. а) Прямые a и b пересекаются. Прямые а и с параллельны. Могут ли прямые b и с , быть скрещивающимися. Ответ обоснуйте.

б) Прямая а параллельна плоскости α, а прямая b пересекает плоскость α . Определите, могут ли прямые а и b быть: а) параллельными б) пересекающимися в) скрещивающимися. Ответ обоснуйте.

7. Плоскость α проходит через основание трапеции ABCD. Точки М и N — середины боковых сторон трапеции.

а) Докажите, что MN // α

б) найдите AD, если ВС = 4 см, MN = 6 см.

8. Прямая СD проходит через вершину С треугольника АВС и не лежит в плоскости (АВС). Точки Е и F – середины отрезков АВ и ВС.

а) докажите, что CD и EF – скрещивающиеся прямые

б) найдите угол между прямыми CD и EF, если угол DCA равен 60 градусов.

9. Нельзя провести плоскость через две прямые, если они….

1) параллельные 2) пересекающиеся 3) скрещивающиеся

10. Какое утверждение неверное?

1) если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость

2) если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая параллельна данной плоскости

3) если две прямые параллельны данной плоскости, то они параллельны друг другу

11. а) Какое утверждение о прямых верное?

2)

3)

б) укажите прямые, скрещивающиеся с прямой А 1 С 1

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Контрольная работа для 6 класса (3 четверть, к учебнику М.З. Биболетовой «Enjoy English 5-6 класс»

Данная работа представляет собой лексико-грамматический тест, позволяющий проверить знания учащихся, полученные за з четверть. Работа включает 9 заданий: задания на проверку лексики по теме Семья»,раз.

Самостоятельная работа для 2 класса (3 четверть)

Самостоятельная работа для учеников 2 класса.

некоторые контрольные и самостоятельные работы для 5 класса

В данной папке я предлагаю Вашему вниманию некоторые контрольные и самостоятельные работы для 6 класса. Они разработаны мной в разные годы с учетом особенностей тех классов, в которых я раб.

некоторые контрольные и самостоятельные работы для 6 класса

Предлагаю Вашему вниманию некоторые контрольные и самостоятельные работы для 6 класса. Они были разработаны мной в раные годы с учетом особенностей тех классов, в которых я работала. Буду рада, если о.

Контрольные и самостоятельные работы по геометрии 10 класс

Данный материал представляет собой контрольные и самостоятельные работы по геометрии 10 класса по учебнику Атанасяна ( 1 полугодие).

Контрольная работа по геометрии за 3 четверть в 7 классе по УМК Атанасян Л.С.

Работа состоит из 7 заданий: 4 задания базового уровня, 5,6,7 повышенного уровня. Работа рассчитана на 45 мин.Критерии оценивания: оценка «5» — за любые правильно выполненные 6 заданий.

Самостоятельная работа для 7 класса по УМК Rainbow 1 четверть

Самостоятельная работа для 7 класса по УМК Rainbow содержит задания на исчисляемые и неисчисляемые существительные, правильное написание лексических единиц по теме «Школьные предметы», знани.

Видео:Параллельность прямых. 10 класс.Скачать

Самостоятельная работа по теме: «Параллельные прямые в пространстве, параллельность прямых и плоскостей» (10 класс)

Видео:Прямые и плоскости 10 классСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Самостоятельная работа по теме: «Параллельные прямые в пространстве. Параллельность прямых и плоскостей»

№1 Отрезок АВ не пересекается с плоскостью α. Через концы отрезка АВ и его середину — точку М — проведены параллельные прямые, пересекающие плоскость α в точках А₁, В₁, М₁.

а) Докажите, что точки А₁, В₁, М₁ лежат на одной прямой;
б) Найдите АА₁, если ВВ₁ = 12 см, ММ₁ = 8 см.

№2 Точки А и В лежат в плоскости α, а точка С не лежат в этой плоскости. Докажите, что прямая, проходящая через середины отрезков АС и ВС, параллельная плоскости α.

№3 Плоскость α проходит через основание AD трапеции ABCD. Точки E и F — середины отрезков AB и CD соответственно. Докажите, что EF|| α.
_____________________________________________________________________________________

№1 Через конец А отрезка АВ проведена плоскость α. Через точку М — середину отрезка АВ — и точку В проведены параллельные прямые, пересекающие плоскость α в точках М₁ и В₁ соответственно.

а) Докажите, что точки А₁, В₁ и М₁ лежат на одной прямой;
б) Найдите ВВ₁, если ММ₁ = 4 см.

№2 Точка М не лежит в плоскости прямоугольника ABCD . Докажите, что прямая CD параллельная плоскости АВМ.

№3 Плоскость α проходит через сторону АС треугольника АВС. Точка D и E — середины отрезков AB и BC соответвенно. Докажете, что DE || α.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

Самостоятельные работы по геометрии 10 класс

Самостоятельные работы по геометрии для 10 класса.

Просмотр содержимого документа
«Ср 1.1 Введение в стереометрию. Аксиомы стереометрии»

Самостоятельная работа 1.1

Введение в стереометрию. Аксиомы стереометрии

А1. Пользуясь изображением на рисунке 1, назовите:

а) точку пересечения прямой AD с плоскостью DD ₁ C ;

б) линию пересечения плоскостей ADD ₁ и D ₁ CD .

В какой из плоскостей ADD ₁, A ₁ B ₁ B , ВВ₁С₁, ВС D не лежит точка А?

А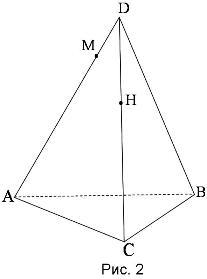2. Перечертите рисунок 2 в тетрадь и постройте:

а) точку пересечения прямой MH с плоскостью АВС;

б) линию пересечения плоскостей MHB и А BC .

В1. Точка О – центр окружности, описанной около треугольника АВС. Принадлежит ли точка С плоскости, в которой лежат точки А, В и О?

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 1.1

Введение в стереометрию. Аксиомы стереометрии

А1. Пользуясь изображением на рисунке 1, назовите:

а) точку пересечения прямой МС с плоскостью В₁В C ₁;

б) линию пересечения плоскостей МС₁С и ВСВ₁.

В каких из плоскостей ADD ₁, ABB ₁, ABD , MD ₁С₁, лежит прямая MD ₁?

А2. Перечертите рисунок 2 в тетрадь и постройте:

а) точку пересечения прямой РК с плоскостью АВС;

б) линию пересечения плоскостей РКС и А DC .

В1. Точка О – центр окружности, описанной около четырехугольника АВС D . Точки А, О и С принадлежат плоскости . Принадлежит ли этой плоскости вершина D ?

Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 2.1 Параллельность прямых, прямой и плоскости»

Самостоятельная работа 2.1

Параллельность прямых, прямой и плоскости

А1. На рисунке 1 точки М, Н и Р – середины соответственно отрезков AD , D В, A С, PK || MH . Найдите периметр четырех угольника МНРК, если АВ = 8 см, С D = 10 см.

А2. Некоторая плоскость пересекает боковые стороны АВ и CD трапеции АВС D в точках М и К соответственно. Докажите, что AD || , если М и К – середины боковых сторон трапеции.

В1. Даны четыре точки А, В, С, D , не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и С D , АС и В D , А D и ВС, пересекаются в одной точке.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 2.1

Параллельность прямых, прямой и плоскости

А1. На рисунке 1 точка А – середина отрезка PK , АВ || С D , В C || AD , В C || PM , CD || HK . Найдите PM и НК, если С D = 16 дм, В C = 8 дм.

А2. Плоскость пересекает стороны ВА и В C треугольника АВС в точках Н и К соответственно. Докажите, что A С || , если Н и К – середины сторон АВ и ВС.

В1. Даны четыре точки А, В, С, D , не лежащие в одной плоскости. Докажите, что любые две из трех прямых, соединяющие середины отрезков АВ и С D , АС и В D , А D и ВС, лежат в одной плоскости.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 2.2 Взаимное расположение прямых в пространстве»

Самостоятельная работа 2.2

Взаимное расположение прямых в пространстве

А1. Точка М не принадлежит плоскости треугольника АВС. Каково взаимное расположение прямых МА и ВС? Ответ обоснуйте.

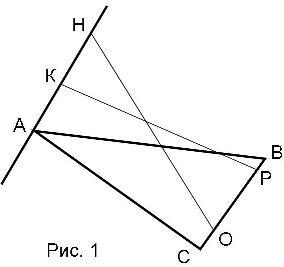
А2. На рисунке 1 прямая НА пересекает плоскость АВС. Каково взаимное расположение прямых ОН и РК? Ответ обоснуйте.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 2.2

Взаимное расположение прямых в пространстве

А1. Точка М не принадлежит плоскости четырехугольника АВС D . Каково взаимное расположение прямых М D и ВС? Ответ обоснуйте.

А2. На рисунке 1 прямая МВ пересекает плоскость АВС. Каково взаимное расположение прямых ОК и РН? Ответ обоснуйте.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 2.3 Параллельность плоскостей. Тетраэдр и параллелепипед»

Самостоятельная работа 2.3

Параллельность плоскостей. Тетраэдр и параллелепипед

А1. Сторона АС треугольника АВС лежит в плоскости . Через середину ВА – точку М проведена плоскость , параллельная плоскости и пересекающая ВС в точке К. Найдите МК, если АС = 10 см.

А2. В тетраэдре DABC постройте сечение плоскостью, проходящей через середину ребра DC , вершину В и параллельной прямой АС.

А3. В параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ точки К, Р и М принадлежат соответственно ребрам АА₁, А₁В₁ и ВС. Постройте сечение параллелепипеда плоскостью КРМ.

Задания А1-А3 соответствуют уровню обязательной подготовки.

Самостоятельная работа 2.3

Параллельность плоскостей. Тетраэдр и параллелепипед

А1. Сторона АВ треугольника АВС лежит в плоскости . Через середину АС – точку Р проведена плоскость , параллельная плоскости и пересекающая ВС в точке Е. Найдите АВ, если РЕ = 7 см.

А2. В тетраэдре DABC постройте сечение плоскостью, проходящей через вершину А, точку М ребра D В, параллельной прямой ВС.

А3. В параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ точки Р, Н и К принадлежат соответственно ребрам В₁С₁, СС₁ и АВ. Постройте сечение параллелепипеда плоскостью РНК.

Задания А1-А3 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 3.1 Перпендикулярность прямой и плоскости»

Самостоятельная работа 3.1

Перпендикулярность прямой и плоскости

А1. ВН – медиана треугольника АВС. Прямая МА перпендикулярна плоскости треугольника. Найдите угол между прямыми ВН и МА.

А2. Прямые АВ и С D перпендикулярны некоторой плоскости и пересекают ее в точках В и В соответственно. Найдите АС, если АВ = 9, CD = 15, BD = 8.

В1. Все грани параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ – равные ромбы; углы между ребрами, имеющими общую точку А равны. Выясните, перпендикулярна ли прямая А₁С прямой B ₁ D ₁ .

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 3.1

Перпендикулярность прямой и плоскости

А1. СЕ – биссектриса треугольника АВС. Прямая BD перпендикулярна плоскости треугольника. Найдите угол между прямыми CE и BD .

А2. Отрезок МН не имеет общих точек с плоскостью. Прямые МР и НО, перпендикулярные этой плоскости, пересекают ее в точках Р и О соответственно, МР = 12 дм, РО = 5 дм, НО = 24 дм. Найдите МН.

В1. В параллелепипеде МРКНМ₁Р₁К₁Н₁ все грани – ромбы;

. Выясните, перпендикулярна ли прямая Р₁Н прямой МК.

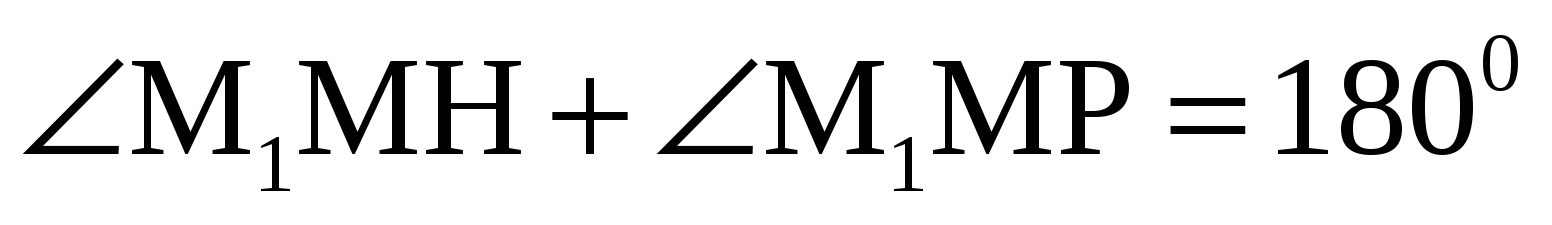
Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 3.2 Перпендикуляр и наклонные»

Самостоятельная работа 3.2

Перпендикуляр и наклонные

А1. В треугольнике АВС АС = ВС = 10 см, 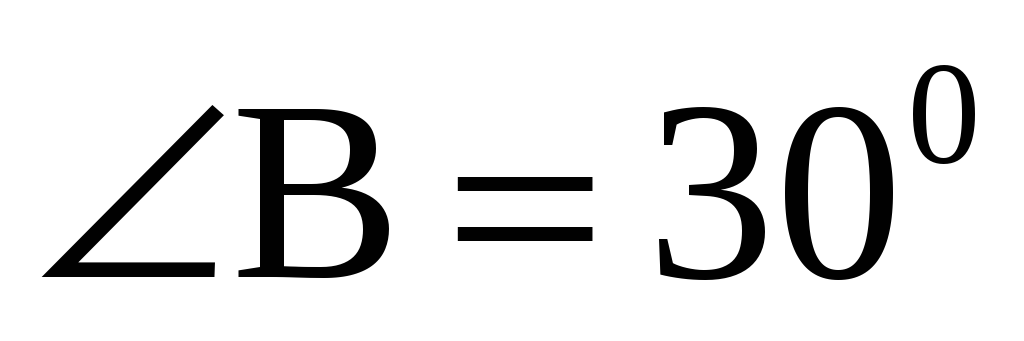. Прямая BD перпендикулярна плоскости треугольника, BD = 5см. Найдите расстояние от точки D до прямой АС и расстояние от точки В до плоскости ADC .

А2. Отрезок АМ является перпендикуляром к плоскости прямоугольника АВС D . Угол между прямой МС и этой плоскостью равен 30 0 , , CD = 2. Найдите АМ .

В1. Даны две параллельные плоскости и множество треугольников таких, что в каждом треугольнике две вершины принадлежат первой из двух данных плоскостей, а третья вершина – второй . Какую фигуру образует множество всех точек пересечения медиан треугольников?

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 3.2

Перпендикуляр и наклонные

А1. В треугольнике АВС угол С прямой, а 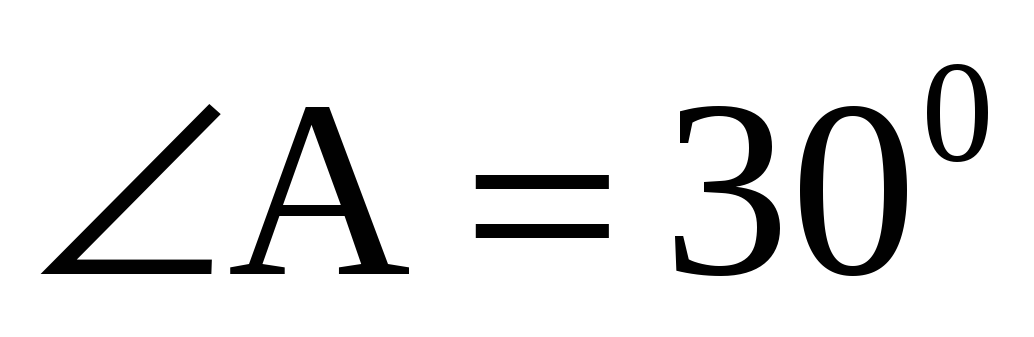. Через точку С проведена прямая СМ, перпендикулярная плоскости треугольника, АС = 18см,

СМ = 12 см. Найдите расстояние от точки М до прямой АВ и расстояние от точки В до плоскости AC М.

А2. Отрезок ВМ является перпендикуляром к плоскости параллелограмма АВС D . Угол между прямой МА и этой плоскостью равен 60 0 . 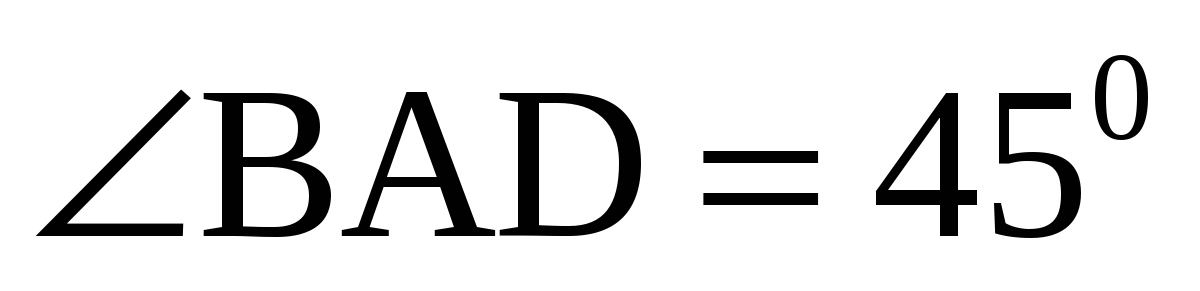, АВ = 20 см. Найдите расстояние от точки М до плоскости АВС.

В1. Даны две параллельные плоскости и и множество треугольников таких, что одна сторона каждого треугольника лежит в плоскости , а середина другой – в плоскости . Какую фигуру образует множество вершин этих треугольников, не принадлежащих плоскости ?

Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 3.3 Перпендикулярность плоскостей»

Самостоятельная работа 3.3

А1. В прямоугольном параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ основание АВ CD – квадрат, 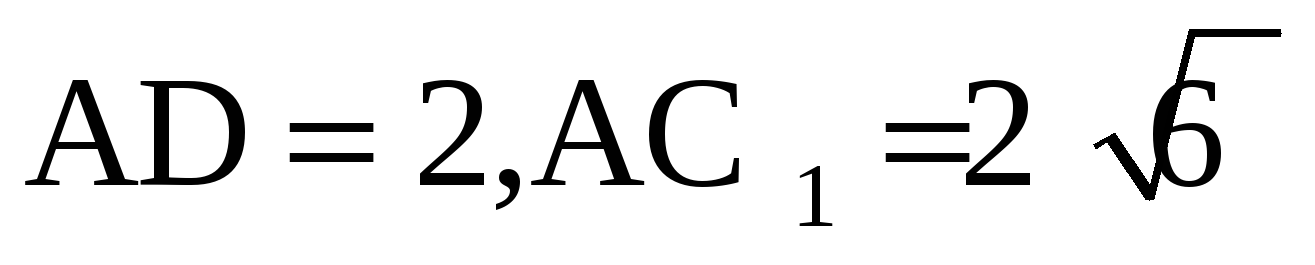. а) Найдите С C ₁. б) Докажите, что плоскости АС C ₁ и В B ₁ D ₁ взаимно перпендикулярны.

А2. Отрезок АМ является перпендикуляром к плоскости прямоугольника АВС D . Угол между прямой МС и этой плоскостью равен 30 0 , 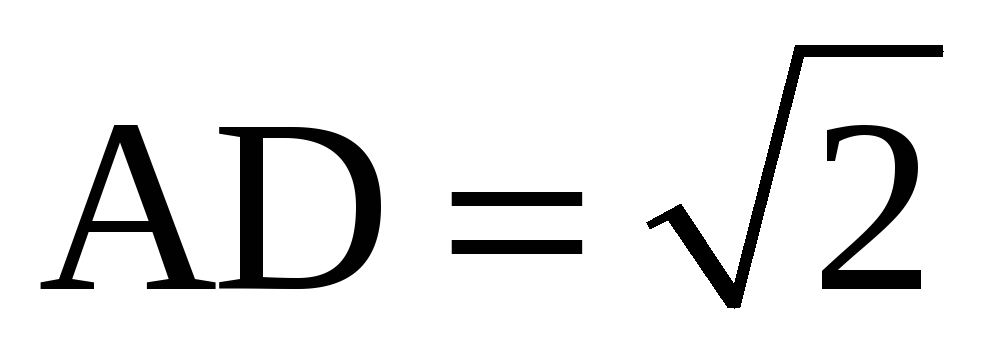, CD = 2. Найдите двугранный угол MCDA .

В1. Точки М, Н и Р – являются соответственно серединами ребер А₁В₁, В₁С₁ и А D куба ABCDA ₁ B ₁ C ₁ D ₁. Периметр сечения куба плоскостью МРН равен . Докажите, что плоскости МНР и В DD ₁ взаимно перпендикулярны.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 3.3

А1. В прямоугольном параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ . а) Найдите А C ₁. б) Докажите, что плоскости А A ₁ C ₁ и АВС взаимно перпендикулярны.

А2. В треугольнике АВС угол С прямой, BC =2. Проекцией этого треугольника на некоторую плоскость является треугольник BCD , 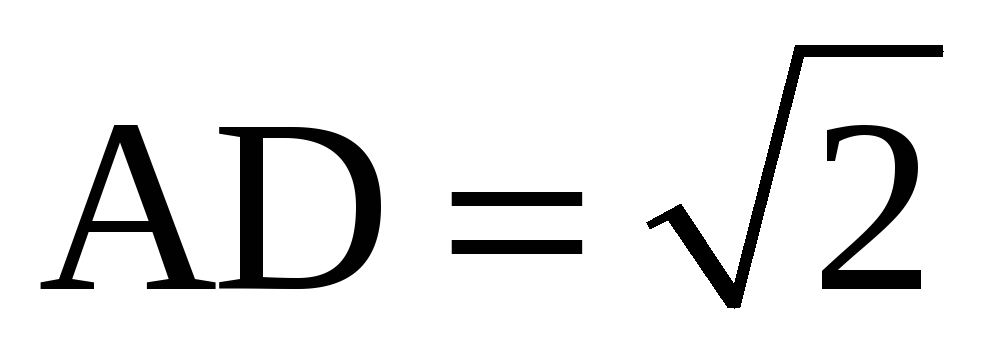, двугранный угол АВС D равен 45 0 . Найдите угол между прямой АС и плоскостью ВС D .

В1. В кубе ABCDA ₁ B ₁ C ₁ D ₁ диагональ . Точки М, Н и Р – середины соответственно ребер B ₁ C ₁, C ₁ D ₁ и DD ₁. Докажите, что плоскости А A ₁ C ₁ и МНР взаимно перпендикулярны.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 4.1 Призма»

Самостоятельная работа 4.1

А1. В правильной треугольной призме длины всех ребер равны 2 см. Найдите площадь сечения, проведенного через боковое ребро и середину противолежащей стороны основания.

А2. В прямом параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ 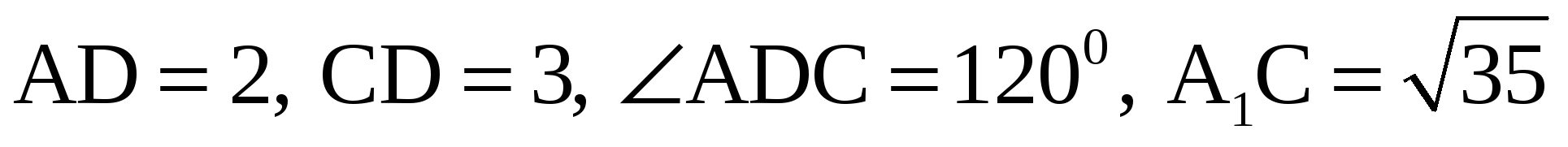. Найдите площади боковой и полной поверхности параллелепипеда.

В1. В наклонной треугольной призме площади двух боковых граней равны

40 см 2 и 80 см 2 . Угол между ними равен 120 о . Найдите площадь боковой поверхности призмы, если длина бокового ребра равна 10 см.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 4.1

А1. В правильной четырехугольной призме ABCDA ₁ B ₁ C ₁ D ₁ сторона основания равна 4 см, а боковое ребро см. Найдите площадь сечения, проведенного через боковое ребро А A ₁ и середину стороны CD основания.

А2. В прямом параллелепипеде ABCDA ₁ B ₁ C ₁ D ₁ 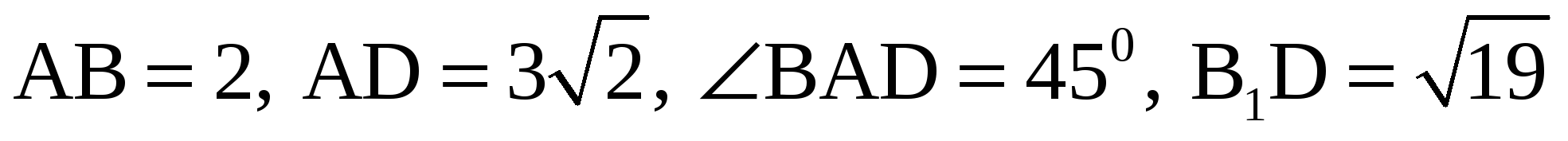. Найдите площади боковой и полной поверхности параллелепипеда.

В1. В наклонной треугольной призме площади двух боковых граней равны

. Угол между ними равен 135 о . Найдите площадь боковой поверхности призмы, если длина бокового ребра равна 3 см.

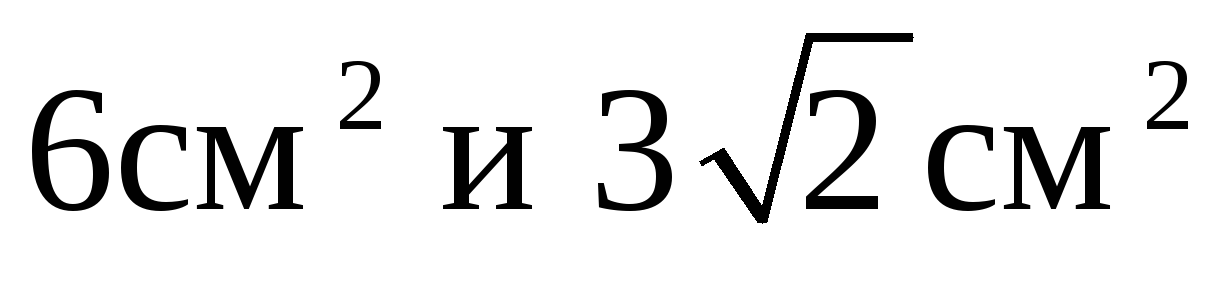
Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 4.2 Пирамида»

Самостоятельная работа 4.2

А1. В правильной четырехугольной пирамиде сторона основания равна 5 см, а высота 7 см. Найдите площадь поверхности пирамиды.

А2. В правильной треугольной пирамиде боковые грани наклонены к плоскости основания под углом 45 о . Расстояние от центра основания до боковой грани равно 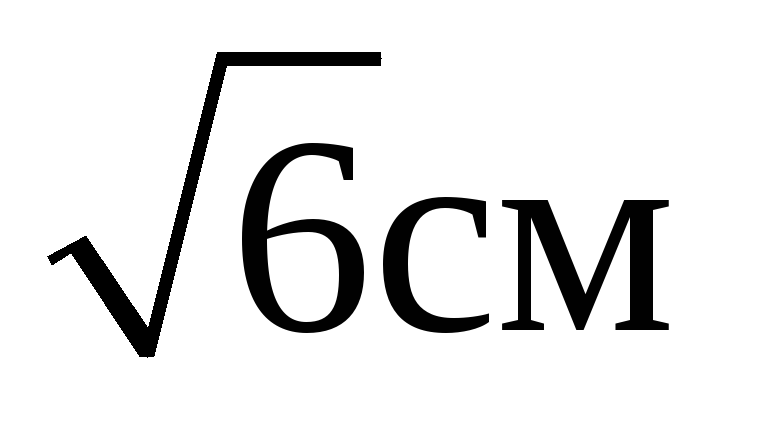. Найдите площадь боковой поверхности пирамиды.

В1. В правильной четырехугольной усеченной пирамиде стороны оснований равны 10 и 8 см, а высота равна 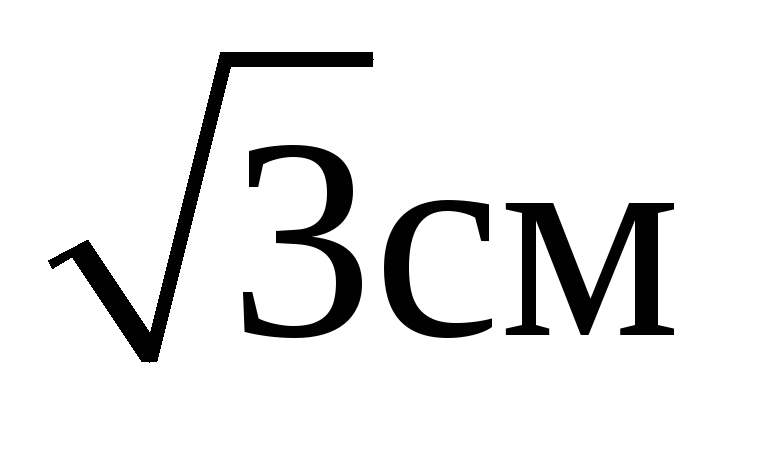. Найдите площадь боковой поверхности пирамиды.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Самостоятельная работа 4.2

А1. В правильной треугольной пирамиде сторона основания равна 4 см, а высота 6 см.. Найдите площадь поверхности пирамиды.

А2. В правильной треугольной пирамиде боковые грани наклонены к плоскости основания под углом 60 о . Расстояние от центра основания до боковой грани равно 2 см. Найдите площадь боковой поверхности пирамиды.

В1. В правильной треугольной усеченной пирамиде стороны оснований равны 6 и 3 см, а высота равна 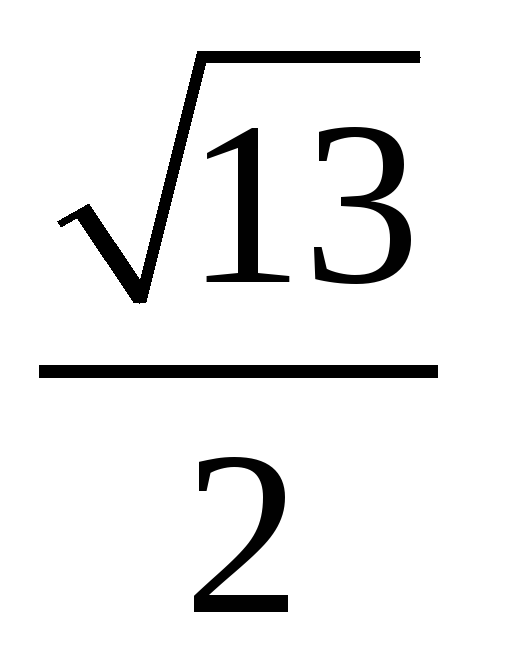см. Найдите площадь боковой поверхности пирамиды.

Задания А1-А2 соответствуют уровню обязательной подготовки.

Просмотр содержимого документа
«Ср 4.3 Правильные многогранники»

Самостоятельная работа 4.3

А1. Найдите площадь поверхности правильного октаэдра, ребро которого равно 4 см.

А2. Ребро куба равно 8 см. Найдите площадь сечения, проходящего через диагонали трех его граней.

А3. Сколько осей симметрии и сколько плоскостей симметрии имеет правильный тетраэдр?

В1. Докажите, что концы двух непараллельных диагоналей противолежащих граней куба являются вершинами тетраэдра.

Задания А1-А3 соответствуют уровню обязательной подготовки.

Самостоятельная работа 4.3

А1. Найдите площадь поверхности правильного октаэдра, ребро которого равно 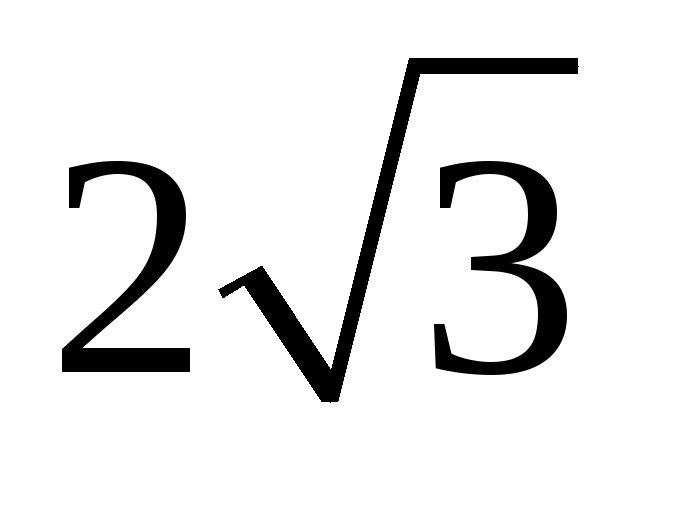см.

А2. Ребро куба равно 10 см. Найдите площадь сечения, проходящего через диагонали двух его граней.

А3. Сколько осей симметрии и сколько плоскостей симметрии имеет куб?

В1. Докажите, что концы двух непараллельных диагоналей противолежащих граней куба являются вершинами тетраэдра.

Задания А1-А3 соответствуют уровню обязательной подготовки.

🔍 Видео

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Геометрия 10 класс Параллельность прямых, прямой и плоскости практикаСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Параллельные прямые в пространствеСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

10 класс - Геометрия - Параллельные прямые в пространстве. Параллельность трёх прямыхСкачать

Параллельность прямой плоскостиСкачать

Подготовка к контрольной работе по теме "Параллельность прямых и плоскостей" 10 класс.Скачать

самостоятельная работа 3. 10 классСкачать

Перпендикулярность прямой и плоскости. 10 класс.Скачать